【论文阅读笔记】ICLR 2025 | 解析Ref-Gaussian如何实现高质量可交互反射渲染

Reflective Gaussian Splatting

Info

会议 【ICLR 2025】

作者 复旦大学，萨里大学；复旦·张力教授团队

Github地址 https://github.com/fudan-zvg/ref-gaussian.git

Project地址 https://fudan-zvg.github.io/ref-gaussian/

Abstract

新视图合成得益于越来越强大的NeRF和3DGS方法，经历了显著的进展。然而，反射物体的重构仍然具有挑战性，缺乏在实现实时高质量渲染的同时处理相互反射的适当解决方案。为填补这一空白，我们提出了一种反射高斯重构（Ref-Gaussian）框架，其特点在于两个组成部分：（I）基于物理的延迟渲染，通过公式化分裂和近似，使渲染方程能够利用像素级的材料属性；（II）基于高斯的相互反射，首次在高斯重构范式中实现所需的相互反射函数。为了增强几何建模，我们进一步引入了材料感知的法线传播和初始的每个高斯阴影阶段，以及二维高斯原语。在标准数据集上进行的大量实验表明，Ref-Gaussian在定量指标、视觉质量和计算效率方面均优于现有方法。此外，我们展示了我们的方法作为反射和非反射场景的统一解决方案，超越了之前仅关注反射场景的替代方案。同时，我们还说明了Ref-Gaussian支持更多应用，如重光照和编辑。

Introduction

近年来，在多视图图像中进行3D物体重构和新视角合成方面取得了巨大的进展。神经辐射场（NeRF）（Mildenhall等，2021）通过神经隐式场表示3D场景，利用体积渲染技术实现高质量、逼真的图像合成。然而，NeRF在最优化和渲染方面计算开销较大，限制了其在实时应用中的使用。为了解决这个问题，Kerbl等人（2023）提出的3D高斯点云（3DGS）通过一组3D高斯来表示场景。它结合了光栅化和α混合，实现了实时和高质量渲染。

然而，大多数NeRF和3DGS在建模反射表面方面面临困难，因为它们固有地无法捕捉高频镜面成分。为了解决这个问题，Ref-NeRF（Verbin等，2022）利用集成方向编码来平滑反射辐射的插值。但是，这种方法未能分解环境照明，使其在重光照方面的应用受到限制。几种NeRF方法（Verbin等，2022；Liang等，2023）面临计算成本和灵活性有限的挑战。在每个高斯上使用简化的阴影函数可以实现快速收敛，但在几何、材料和照明建模中却遭受了大量噪声（GSShader）。为避免此问题，在像素级别执行阴影函数（即延迟阴影），并通过阿尔法混合来平滑梯度是有帮助的（3DGS-DR）。然而，限制使用简化的阴影函数使其在建模具有复杂结构和表面的复杂反射物体及其相互反射现象时效果不佳。为了解决后者，RelightableGaussian（Gao等，2023）通过高斯追踪射线以推断可见性，但代价是产生大量噪声和增加了来自蒙特卡罗采样的计算开销。

为了综合解决上述问题，我们提出了一种反射高斯喷溅（RefGaussian）框架，该框架能够实时高质量地渲染反射物体，同时考虑复杂的相互反射效应。这得益于两个关键组件：（I）基于物理的延迟渲染，我们通过像素级的材料属性（例如双向反射分布函数，简称BRDF）增强了渲染方程，并采用分裂和近似来避免使用蒙特卡罗采样时的高计算量；（II）基于高斯的相互反射，我们首次利用高斯喷溅实现了复杂的相互反射函数，尽管提取网格的准确性面临挑战。为了增强几何建模，我们选择了二维高斯原件作为场景表示，同时引入了初始的每个高斯阴影阶段（在高斯级别进行阴影处理以提供良好的几何初始化），以及一种关注材料的法线传播过程（扩大具有高金属度和低粗糙度的高斯的尺度）。

我们做出了以下贡献：(I) 我们努力实现具有相互反射的反射物体的实时高质量渲染，适用于三维空间。(II) 我们创新了一种通用的三维重构框架——反射高斯溅射（Ref-Gaussian），其特点是基于物理的延迟渲染和高斯基础的相互反射。该方法通过几何聚焦的最优化进一步增强，包括采用二维高斯基元、考虑材料的法线传播和逐高斯的阴影初始化。(III) 大量实验表明，Ref-Gaussian在反射和非反射场景中，在定量指标、视觉质量和计算效率方面优于之前的方法，同时支持下游应用，如重光照和编辑。

Related Work

在本文中，受到3DGS-DR的启发，我们采用了像素级的延迟阴影技术，但使用BRDF特性来执行渲染函数，以处理复杂场景。此外，我们建议对提取的网格进行光线追踪，以计算我们渲染方程中高光成分的可见性。结合渲染方程的分裂和近似，我们在保持快速渲染速度的同时，建模了相互反射效应。

Method

关于 3DGS 和 2DGS 的预备知识就不在这里重复了。

基于物理的延迟渲染

我们基于物理的延迟渲染采用了简化版的迪士尼BRDF模型（Burley和Studios，2012）。具体而言，每个高斯都与一组与材料相关的属性相关联，包括反射率 $\lambda \in [0,1{]}^3$、金属度 $m\in [0,1]$和粗糙度 $r\in [0,1]$。法向量 $n\in [0,1{]}^3$可以通过每个二维高斯的切向量推导得出，计算公式为 $n=t_u\times t_v$。我们在通过alpha混合获得的像素级特征图上部署渲染方程：

$$\mathbf{X}=\sum _{i=1}^N{\mathbf{x}}_i{\alpha }_i\prod _{j=1}^{i-1}\left(1-{\alpha }_j\right),\text{ where }\mathbf{X}=\left[\begin{array}{c}\mathbf{\Lambda }\\ M\\ R\\ \mathbf{N}\end{array}\right],{\mathbf{x}}_i=\left[\begin{array}{c}{\lambda }_i\\ m_i\\ r_i\\ {\mathbf{n}}_i\end{array}\right]$$

请注意，与在进行 alpha 混合之前直接对高斯进行阴影处理（GSshader）不同，我们的延迟着色将 alpha blending 视为一种平滑滤波器。这使得特征的最优化得以稳定，并最终产生更具一致性的渲染结果。

通过聚合材料图，包括反射率$\Lambda$、金属度$M$、粗糙度$R$和法线$N$，随后应用渲染方程。渲染方程表示在方向${\omega }_o$上发出的辐射亮度$L({\omega }_o)$为：

$$L\left({\omega }_o\right)={\int }_{\Omega }{L}_i\left({\omega }_i\right)f\left({\omega }_i,{\omega }_o\right)\left({\omega }_i\cdot \mathbf{N}\right)d{\omega }_i$$

其中 $f({\omega }_i,{\omega }_o)$ 表示双向反射分布函数（BRDF）。它表示在半球上反射入射光的积分。由于 BRDF 包含漫反射和镜面反射两个部分，因此积分也可以分为两个部分。漫反射项通过查询预积分环境图并使用法向量 N 进行计算，再与材质项相乘，而镜面反射项则需要更复杂的反射计算来考虑表面反射。在这里，我们关注镜面成分，BRDF 的镜面项为：

$$f_s\left({\omega }_i,{\omega }_o\right)=\frac{DGF}{4\left({\omega }_o\cdot \mathbf{N}\right)\left({\omega }_i\cdot \mathbf{N}\right)},$$

其中 D、F 和 G 分别表示 GGX 正态分布函数、菲涅尔项和阴影遮蔽项。

为了计算上述积分项，典型的方法是如(Gao et al., 2023)所示的蒙特卡罗采样。然而，这在实时渲染中计算成本很高。相反，我们采用分裂和近似方法(Munkberg et al., 2022)：

$$L_s\left({\omega }_o\right)\approx {\int }_{\Omega }{f}_s\left({\omega }_i,{\omega }_o\right)\left({\omega }_i\cdot \mathbf{N}\right)d{\omega }_i\cdot {\int }_{\Omega }{L}_i\left({\omega }_i\right)D\left({\omega }_i,{\omega }_o\right)\left({\omega }_i\cdot \mathbf{N}\right)d{\omega }_i\text{\hspace{1em}(8)}$$

第一个项仅依赖于 (ωi · N) 和粗糙度 R，这使得结果可以预先计算并存储在 2D 查找纹理图中。第二个项表示入射辐射在镜面光斑上的积分，可以在每次训练迭代开始时以不同的粗糙度水平进行预积分。这使得可以有效地使用一系列立方图来表示环境光照，通过使用反射方向和粗糙度作为参数进行三线性插值。

GAUSSIAN GROUNDED 互反射

互反射在渲染反射物体中起着关键作用。为此，我们通过分别建模直接光 $L_{dir}$（方程 8 中的第二项）和间接光 $L_{ind}$ 来进一步增强镜面光成分。直接光 $L_{dir}$ 是指没有被任何场景元素阻挡的反射光，其余部分定义为间接光 $L_{ind}$。

具体来说，我们根据入射光是否在反射方向$R=2(w_o\cdot N)N-w_o$上自遮挡来近似可见度V ∈ {0, 1}。我们将来自遮挡部分的间接光表示为$L_{ind}$：

$$L_s^{\prime }\left({\omega }_o\right)\approx \left({\int }_{\Omega }{f}_s\left({\omega }_i,{\omega }_o\right)\left({\omega }_i\cdot \mathbf{N}\right)d{\omega }_i\right)\cdot \left[L_{\mathrm{dir}}\cdot V+L_{\mathrm{ind}}\cdot (1-V)\right]\text{\hspace{1em}(9)}$$

直观上，这里引入的间接光成分$L_{ind}$旨在有效建模环境光照估计中由于遮挡引起的扰动。沿着高斯基元的光线计算可见性并非易事。在此，我们提出在提取的网格上动态进行光线追踪。在优化过程中，我们定期使用截断带符号距离函数（TSDF）融合提取物体的表面网格。一旦构建了网格，我们就使用光线追踪计算光线与表面之间的交点，从而确定每个像素是否被遮挡。为了提高效率，我们采用边界体积层次（BVH）来加速可见性检查的光线追踪过程。至于直接光照Ldir，它仅对应于公式8中的第二项，按照前一部分的描述进行处理。

对于间接光照成分，每个高斯被分配一个额外的视图依赖颜色$l_{ind}$，该颜色由球面谐波建模。在渲染过程中，$l_{ind}$在高斯级别的反射方向上进行评估，并应用 alpha 混合以汇总间接光照图，如下所示:

$$L_{\mathrm{ind}}=\sum _{i=1}^N{l}_{\mathrm{ind}}{\alpha }_i\prod _{j=1}^{i-1}\left(1-{\alpha }_j\right)$$

GEOMETRY FOCUSED MODEL OPTIMIZATION

为了促进我们的物理基础渲染，我们在最优化过程中通过以下设计进一步增强潜在几何体。

初始阶段采用每个高斯着色。由于平滑梯度带来的代价，像素级阴影在初始阶段面临收敛挑战，因为阴影函数干扰了几何体的梯度方向。为了解决这个问题，我们提出了一个专门的初始阶段，在该阶段渲染方程直接应用于每个高斯基元，利用与之相关的材料和几何属性来计算出射辐射。然后，在光栅化过程中对出射辐射进行α混合，以生成最终的PBR渲染。这种高斯级阴影设计可以更有效地将梯度传递回高斯基元，并最终促进最优化过程。

材料感知的法线传播 在法线不准确的位置，往往难以捕捉到显著的镜面成分，因为其对反射方向的内在敏感性。我们观察到，在Ref-Gaussian中，法线准确性与高金属、低粗糙度特性之间存在强正相关（这是一个镜面成分显著的典型情况）。在这一见解的基础上，我们建议定期增加具有高金属度和低粗糙度的二维高斯的尺度，以便其法线信息能够传播到相邻的高斯，从而捕捉更精确的几何形状。

我们设计了一个以几何为重点的目标函数：$L=L_c+{\lambda }_n{L}_n+{\lambda }_{smooth}{L}_{smooth}$，其中$Lc=(1-\lambda )L_1+\lambda L_{D-SSIM}$是RGB重构损失，我们设置平衡权重λ = 0.2（Kerbl等，2023）。

第二项 $L_n=1-{\tilde{\mathbf{N}}}^{\mathrm{T}}\mathbf{N}$ 是Normal一致性损失。它通过最小化渲染法线 N（通过 alpha 混合获得）与来自深度图的表面法线$\tilde{N}$之间的余弦差异，鼓励高斯与表面对齐。第三项 $L_{smooth} = ∥∇N ∥ exp(−∥∇Cgt∥) $是一种边缘感知的法线平滑损失。它旨在正则化低纹理区域的法线变化。

Experiments

为了评估Ref-Gaussian在新视角合成、几何体、材料和光照重构及下游应用中的性能，我们进行了系列定量和定性实验。此外，我们在补充材料中提供了一段演示视频，展示了Ref-Gaussian在两个合成数据集上的动态渲染，并进行了比较分析。我们选择了两个合成数据集，分别是Shiny Blender（Verbin等，2022）和Glossy Synthetic（Liu等，2023），用于反射物体的新视角合成，同时选择Ref-Real数据集（Verbin等，2022）用于真实世界的开放场景。我们比较了反射3D重构领域中的几个代表性模型，包括Ref-NeRF（Verbin等，2022）、ENVIDR（Liang等，2023）、3DGS（Kerbl等，2023）、GaussianShader（Jiang等，2024）、可重光照高斯（RelightableGaussian，R3DG）（Gao等，2023）和3DGSDR（Ye等，2024）。我们还与更多基于NeRF的模型进行了比较，如NeRO（Liu等，2023）、NeuS（Wang等，2021）和NDE（Wu等，2024），详见附录中的表5和表6。评估指标方面，我们使用了三个标准指标：PSNR、SSIM（Wang等，2004）和LPIPS（Zhang等，2018）。

实现细节 我们的训练程序分为两个阶段。我们在初始阶段使用高斯渲染进行了18,000步的训练，随后进入延迟渲染阶段，训练约40,000步。在第二阶段之前，我们重置所有颜色和材质属性，仅保留高斯的几何形状。可训练材质属性（金属度、粗糙度和反照率）的学习率均设置为0.005，而环境贴图的学习率设置为0.01。其他基本可训练属性，如位置和协方差，与2DGS（Huang等人，2024）一致。然后，我们对金属度不低于0.02且粗糙度不高于0.1的高斯进行材质感知法线传播。此外，我们采用来自3DGS-DR（Ye等人，2024）的金属初始值，并将初始粗糙度值设置为0.1。在物理基础渲染的实现过程中，我们发现球谐函数的拟合能力优于集成漫反射光，因此我们使用球谐函数进行替代。对于损失函数，${\lambda }_n$设置为0.05，${\lambda }_{smooth}$设置为1.0。此外，我们定期以3000步的间隔提取对象的表面网格。所有实验均在单个NVIDIA A6000图形处理器上进行。

Comparisons

新视角合成 在表1中，我们展示了多个竞争者以及Ref-Gaussian在多个数据集上的新视图合成任务的定量结果。Ref-Gaussian在大多数场景中达到了最先进的性能，尤其是在光滑合成数据集上有显著的改善，这些数据集以反射表面为主。

如图3所示，3DGS（Kerbl等，2023）在处理高频的视角依赖效应时遇到困难，导致在多视角场景中（如Bell）反射表面出现明显的模糊。GShader（Jiang等，2024）引入了显著的噪声，导致失真。3DGS-DR（Ye等，2024）采用简化的阴影函数，但在准确建模复杂的反射场景方面面临挑战，如在Luyu和头盔上的粗糙有色面罩所观察到的。相比之下，Ref-Gaussian有效地克服了这些挑战，提供了精准的环境光建模和对复杂几何体和材料的稳健处理。

此外，在图4中，我们展示了现实场景的定性比较（Verbin等，2022）。Ref-Gaussian提供了更准确的法线图和光照，捕捉到了反射表面上的微妙细节。具体而言，花园球体上的反射现象和轿车窗户上的反射尤为明显。我们在图4中展示了Ref-Gaussian更具物理准确性的反射细节捕捉能力。

材料、法线和光照估计 在表2中，我们对竞争者在法线贴图、环境贴图和效率方面进行了定量比较。Ref-Gaussian 展示了优越的几何重构如高质量的法线图所示。这一改进主要归因于第3.3节讨论的精心设计的几何优化策略。

如图5所示，我们的法线图平滑，其他分解的材质图也是如此。此外，我们的可见性图清晰，准确突出反射方向上被遮挡的区域。Ref-Gaussian在估计环境光照方面也在竞争者中取得了最佳结果，这一评估是在缩放后进行的，以消除分歧。

图6展示了估计环境图的定性比较。与之前的方法相比，我们的结果在细节和整体色调上与真实值更为接近，同时噪声量最少。这一改进可归因于Ref-Gaussian中采用的精确几何和全面建模。

消融实验

我们提供了Ref-Gaussian的定量消融研究。

基于物理的渲染 将BRDF属性分配给高斯函数极大增强了它们表示复杂场景的能力。与3DGS-DR（Ye等，2024）中仅使用一个反射方向向量来查询环境地图的简化阴影函数相比，Ref-Gaussian在学习具有材料变化的场景时表现出显著更好的性能，例如球体上的粗糙带（图7）和头盔上的面罩（图3）。

此外，基于物理的渲染有助于几何重构，这一点在表3的结果中得到了验证。

基于高斯的相互反射 如图9所示，我们的相互反射组件对Tbell和Bell的头部部分影响尤为明显。通过光线追踪可见性，我们成功地重构了新视图合成的间接光照。需要注意的是，相互反射在光泽合成数据集中是少数，其效果在表4中无法完全观察到。

延迟渲染 我们在每个高斯层级进行基于物理的渲染，并观察到反射细节的建模明显变得模糊。如表4所示，未进行延迟渲染时，渲染输出的所有质量指标显著下降。

2D高斯原语 如附录中的图8、表3和表7所示，强调了2D高斯原语在更精确的几何表示方面相对于3D替代品的优越性。这是因为3D高斯在体积辐射表示上与表面的薄特性相冲突。值得注意的是，将2D高斯替换为3D高斯，并保持其他组件不变时，Ref-Gaussian在Shiny Blender（Verbin et al., 2022）和Glossy Synthetic（Liu et al., 2023）数据集上的表现依然出色，如附录中的表7所示。

逐高斯的着色初始化 在初始阶段使用基于物理的渲染提供了在几何收敛的速度和准确率方面显著的优势。当我们用相同数量的步骤替换初始阶段为基于物理的延迟渲染时，最终结果在各项指标上显示了渲染质量和法线重构质量的下降。材料感知法线传播加速了光滑表面的收敛。

表3和表4中呈现的定量比较展示了其在几何重构中的有效性。如图10所示，光滑表面容易发生几何崩溃，但我们的材料感知法线传播有效解决了这个问题。

材料感知法线传播 材料感知法线传播加速了光滑表面的收敛。表3和表4中提供的定量比较展示了其在几何重构中的有效性。如图10所示，光滑表面容易发生几何崩溃，但我们的材料感知法线传播有效地解决了这个问题。

总结

在本文中，我们介绍了一种新颖的高斯溅射框架——Ref-Gaussian，该框架旨在实时高质量地重构反射物体/场景。这是通过构建两个集成组件实现的：基于物理的延迟渲染和高斯基础的相互反射，以及聚焦几何的模型优化。我们还展示了选择基础表示模型的重要性，其中2DGS优于3D替代方案。在多个数据集上的广泛实验表明，Ref-Gaussian在定量指标、视觉质量和效率方面优于现有方法。此外，我们还展示了Ref-Gaussian在重新照明和编辑等其他应用中的效果。

Appendix

Limitations

由于Ref-Gaussian是专门为重建反射场景而设计的，因此在处理非镜面场景时可能表现不佳。在建模相互反射时，我们仅考虑反射方向上的可见性，以近似整个镜面叶片的总体可见性。虽然这种方法显著降低了渲染的计算复杂性，但由于近似的固有不准确性，它可能会在材料估计中引入一些噪声。

重新照明和编辑的定性结果

在非镜面数据集上的进一步定量比较

根据设计，Ref-Gaussian 在反射和非反射场景中均表现出色，使其成为建模各种具有不同反射特性的场景的统一解决方案。这是因为，如公式9所述,内部反射仅作为一个附加元素纳入镜面成分中。因此，在反射较弱的场景中，内部反射的影响自然减弱，并随着金属属性的降低而相应减小。在这种情况下，漫反射成分取而代之，包含任何（通常相对微弱的）内部反射效应的捕捉，以实现最佳性能。

这种行为在附录中的图5和图14所提供的分解结果中显而易见。相比之下，以前专注于反射的替代方案，如 3DGS-DR（Ye et al., 2024），专门设计用于反射场景，这导致了应用范围的缩小。

为了支持这一说法，我们在附录中包含了表8，展示了在主要由非反射场景组成的 NeRF-Synthetic 数据集（Mildenhall et al., 2020）上，Ref-Gaussian、3DGS-DR（Ye et al., 2024）和 3DGS（Kerbl et al., 2023）之间的逐场定量比较，以进行新视图合成。结果表明，我们的 Ref-Gaussian 仍然优于这两种替代方案，验证了其通用和统一的优势。

基于Nerf方法的额外基线

间接成分对REF-REAL数据集的定性结果

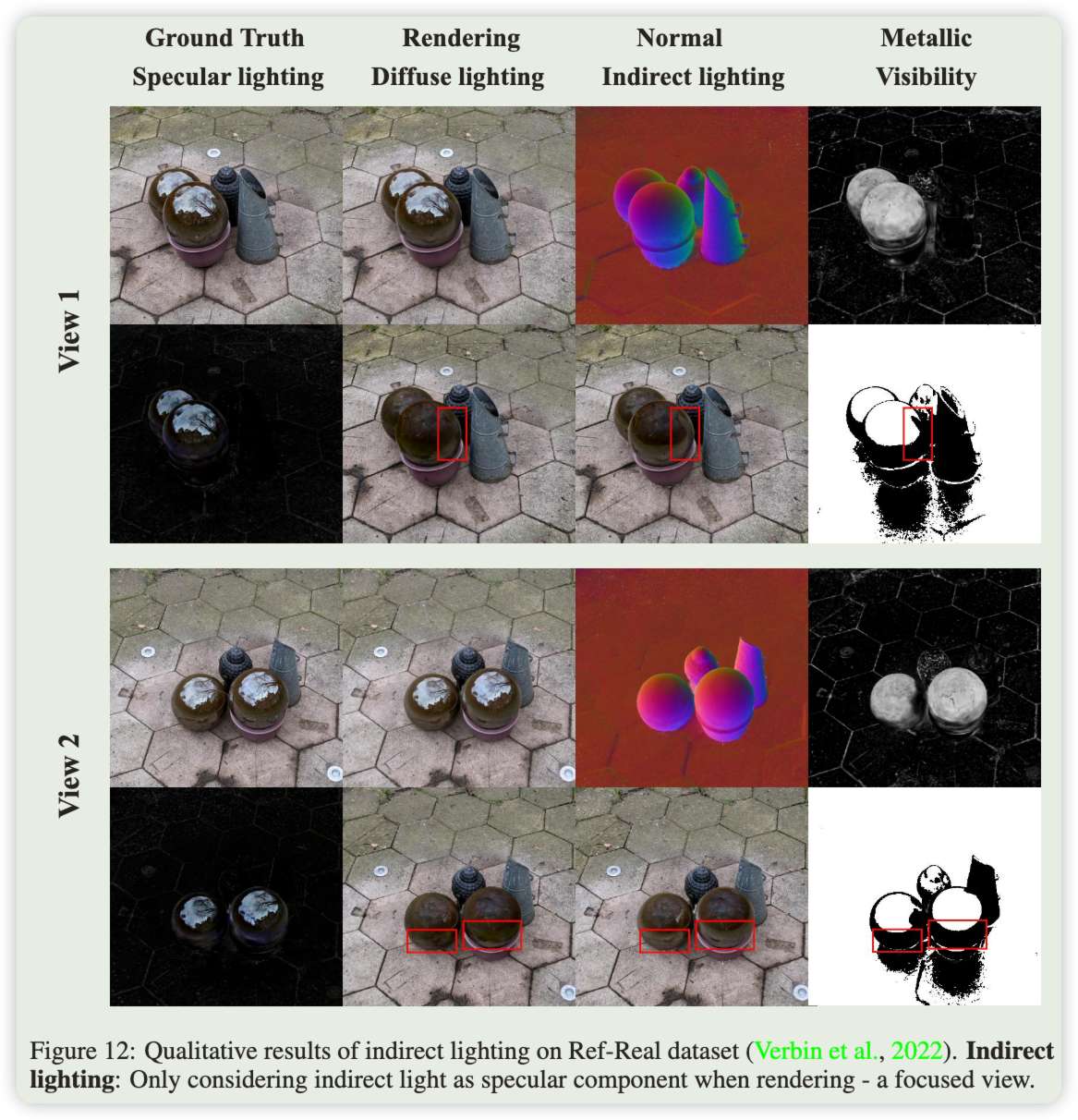
我们在图12中提供了更丰富的定性结果，其中多个物体提供了丰富的相互反射。可以观察到，在新视图合成的任务中，三个组件——漫反射、镜面反射和间接光——有效地互为补充，共同产生了出色的最终渲染结果。具体而言，基于金属属性，漫反射组件主要对石球外部的非反射物体和地面细节进行建模。镜面反射组件则关注石球上那些反射光未被地面或其他物体遮挡的部分，捕捉细致的反射细节，而间接光组件有效捕捉地面和邻近物体的投影。这些分解结果强烈表明，Ref-Gaussian即使在复杂的现实场景中，也能通过其精心设计的渲染方法和精确的几何重构，准确捕捉各种细节。

综合2DGS消融研究的定量结果

为了明确展示2DGS表示的效果，并更公平、全面地证明Ref-Gaussian相对于其他技术的优越性，我们将Ref-Gaussian的2DGS表示替换为3DGS，同时保持其他部分不变以进行比较，如表7所示。2DGS的引入显著增强了模型的性能。值得强调的是，基于3DGS构建的Ref-Gaussian在Shiny Blender（Verbin等，2022）和Glossy Synthetic（Liu等，2023）数据集的大多数场景中也表现出色，进一步突显了该渲染模型的内在优越性。

几何重构的定性结果

我们进一步展示了我们在几何重构方面的优势（图13，14）。图13中的定性比较表明，Ref-Gaussian对细节的全面把握优于其他先进技术（例如汽车的轮胎和咖啡中的水面）。