力扣:基本计算器
基本计算器:
224. 基本计算器 - 力扣(LeetCode)

本体思路为,将中缀表达式转为后缀表达式,通过后缀表达式进行运算。
中缀表达式:
我们日常生活中熟知的表达式如1+2-3=0 就是一个中缀表达式。
后缀表达式:
150. 逆波兰表达式求值 - 力扣(LeetCode)

后缀表达式(Postfix Expression),也称为逆波兰表示法(Reverse Polish Notation, RPN),是一种数学表达式的表示方法。在这种表示法中,运算符紧跟在操作数之后,而不是像中缀表达式(如 3 + 4)那样将运算符放在操作数中间。
中缀表达式:常规的数学表达式,如 3 + 4 * 2。
后缀表达式:运算符放在操作数之后,如 3 4 2 * +。
后缀表达式运算:
后缀表达式运算思想为,遇到操作数,入栈,遇到操作符,则弹出栈顶的两个元素,进行操作符匹配运算,当表达式结束后,留在栈顶的操作数就是最后的值。
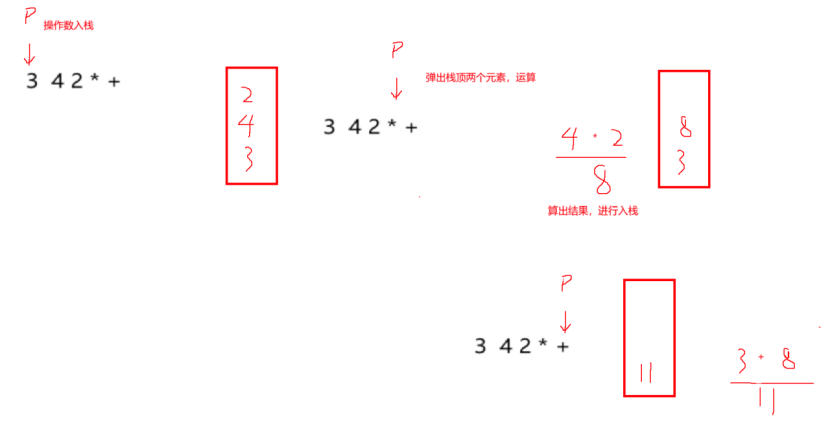

这里将元素弹出时候,需要进行左元素与右元素区分,因为如果是+*则左元素与右元素没区别,但如果是-/,谁在左,谁在右,区别就很大。
中缀转后缀:
中缀想要转成后缀需要把握两个思想
- 遇到操作数载入容器
- 遇到操作数,判断操作数的优先级,进行入栈
- 如果栈里没有操作符,则直接入栈
- 如果栈顶操作符优先级比当前操作符优先级低,则当前操作符入栈
- 如果比当前栈顶操作符优先级低或相等,这表示前面的操作符可以进行运算,弹出当前栈顶操作符,载入容器。将当前操作符继续入栈。

如果遇到,( ),我们可以将它看作为一个子表达式,进行递归运算。

以下是代码实现:
#include<iostream>
#include<map>
#include<vector>
#include<stack>
#include<functional>
#include<algorithm>
#include<string>
using namespace std;class Solution
{
public:void TrunSuffix(string& s, size_t& i, vector<string>& ret){stack<char> st;map<char, int> mp{ {'+',1},{'-',1} ,{'*',2} ,{'/',2} };while (i < s.size()){if (isdigit(s[i])){string num;for (; i < s.size(); i++){if (isdigit(s[i])){num += s[i];}else{break;}}ret.push_back(num);}else if (s[i] == '('){TrunSuffix(s, ++i, ret);}else if (s[i] == ')'){++i;while (!st.empty()){char ch = st.top();st.pop();ret.push_back(string(1, ch));}return;}else{if (st.empty() || mp[st.top()] < mp[s[i]]){st.push(s[i++]);}else{char ch = st.top();st.pop();ret.push_back(string(1, ch));st.push(s[i++]);}}}while (!st.empty()){char ch = st.top();st.pop();ret.push_back(string(1, ch));}}int Suffix(vector<string>& ret){map<string, function<int(int, int)>>mp ={{"+", [](int a, int b) {return a + b; }},{ "-", [](int a, int b) {return a - b; } },{ "*", [](int a, int b) {return a * b; } },{"/", [](int a, int b) {return a / b; }}};stack<int> st;for (auto& e : ret){if (mp.count(e)){int right = st.top();st.pop();int left = st.top();st.pop();int r = mp[e](left, right);st.push(r);}else{st.push(stoi(e));}}return st.top();}int calculate(string s){//1+2-(3*4)string news;for (size_t j = 0; j < s.size(); j++){if (s[j] != ' '){news += s[j];}}s.swap(news);news = "";for (size_t j = 0; j < s.size(); j++){if (s[j] == '-' && (j == 0 || (!isdigit(s[j - 1]) && s[j - 1] != ')'))){news += "0-";}else{news += s[j];}}s.swap(news);news = "";int flag = 0;for (int i = 0; i < s.size(); i++){if (s[i] == '+' || s[i] == '-' || s[i] == '*' || s[i] == '/')flag = 1;}if (!flag){string news;for (auto& e : s){if (isdigit(e)){news += e;}}return stoi(news);}vector<string> ret;size_t i = 0;TrunSuffix(s, i, ret);return Suffix(ret);}
};int main()
{int n= Solution().calculate( "(1+(4+5+2)-3)+(6+8)" );cout << n << endl;return 0;
}说一下我在写这题的坑:
- 这题力扣一开始会给出 “1 + 2 +( 4 - 5)”类似这种带空格的表达式,所以在一开始的时候就需要先过滤一遍表达式,将删除空格。

- 我们还需要确认,是负数还是减号,如果是负号,妥妥的会坑。

所以,我们还需要在” - ” 加以判断,如果-前面是操作数,则是正常-号。如果是操作符表示是一个负数,所以我们在直接添加 ”-0”

添加成 0- 就更好的进行运算。
这里还有一个特殊案例

-号前面是 ) 而我们代码会识别成这是一个负数,就会变成

所以还需要特殊判断,如果是 ) 则不进行添加 “0-”

- 力扣给的测试用例里会有(1231231)类似这种。如果不特殊判断,则会直接取到1,及栈顶元素。所以我们在修正完字符串后进行检查,如果没有操作符直接进行返回。
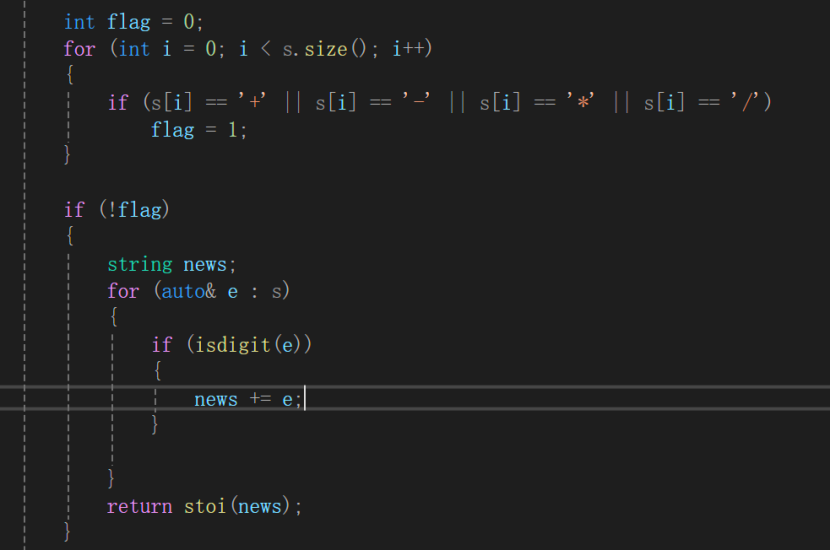
最后,我们可能会在调试期间,进行输出打印。所以在提交答案时候,请将输出打印注释,否则在最后几个测试用例里会有非常长的表达式,会导致超出运行时间,过不了。
