「ECG信号处理——（17）基于小波熵阈值的R峰检测（与时域-频域-多尺度小波法对比）」2025年6月12日

1、引言

        心电图（ECG）信号特征检测旨在准确识别心电图中的关键波形（如P波、QRS波群、T波）及其特征点（如R波峰值）。然而，ECG信号易受噪声干扰（如肌电干扰、基线漂移、工频干扰），且个体差异导致特征形态变化，增加了检测难度。传统方法在复杂噪声环境下检测精度有限，而基于小波熵阈值的方法结合小波变换多分辨率分析与信息熵理论，能更好平衡噪声抑制与特征保留。因此，本文档介绍一种基于小波熵阈值的ECG特征检测方法。

2. 小波熵阈值法

        小波熵阈值法是一种先进的ECG特征检测方法，它巧妙地将小波变换的多分辨率分析能力与信息熵理论相结合。小波变换能够将信号分解到不同尺度，每个尺度的细节系数反映了信号在特定频率范围内的特征。而信息熵则提供了一种量化信号信息分布的方式，通过计算各尺度小波系数的能量占比，可以动态地为每个尺度分配权重。这种方法不仅能够突出QRS波群的特征，还能有效抑制噪声干扰，提高检测的准确性和鲁棒性。

        小波熵阈值法的处理流程如下：

2.1 预处理阶段

        首先对原始ECG信号进行预处理，包括去噪和极性校正，以去除噪声并确保信号的极性一致性。去噪过程采用小波去噪技术，利用db8小波对信号进行六层分解，对细节系数进行软阈值处理，从而抑制噪声。

 （1）去噪：

• 带通滤波：采用三阶巴特沃斯带通滤波器，滤波范围为0.5-45Hz，去除高频噪声和低频漂移。

• 小波去噪：利用db8小波对信号进行六层分解，采用全局阈值法对细节系数进行软阈值处理，抑制噪声。

• 全局阈值计算基于稳健中位数估计：

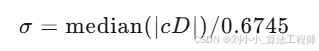
        其中，σ为噪声标准差估计，N为信号长度。

• 软阈值处理公式为：

（2）极性校正：

        对转换后的ECG信号进行预处理，包括去均值操作以消除直流偏移。分析信号前2秒确定极性，若信号最小值绝对值大于最大值，则反转信号极性。

% 自动极性校正
[~,max_loc] = max(ecg(1:min(Fs*2,N))); % 分析前2秒确定极性
[~,min_loc] = min(ecg(1:min(Fs*2,N)));
if abs(ecg(min_loc)) > abs(ecg(max_loc))ecg = -ecg;disp('信号极性已自动校正');
end

图1：数据预处理结果

2.2 小波分解

        选用db8小波对预处理后的ECG信号进行六层分解。db8小波具有较长的滤波器长度，能够提供更好的频率分辨率，适合捕捉ECG信号中的细节特征。小波分解的过程是通过不断分解信号的低频部分，得到不同尺度下的近似系数和细节系数。具体来说，每一层分解都将信号分为低频的近似部分和高频的细节部分。六层分解后，可以获得从高频到低频的不同尺度下的信号特征。采用db8小波对去噪后的ECG信号进行六层分解，获取不同尺度下的近似系数和细节系数。

        其中，x 为输入信号，level 为分解层数，wname 为小波基函数名称。

        相关内容略，详情见我博客👇

「ECG信号处理——（7）小波变换（WT）」2025年1月20日_卷积去除基线漂移-CSDN博客

图2：小波多尺度分解结果

2.3 关键尺度重构 

        根据QRS波群的频段特性，我们知道QRS波群主要集中在8-16Hz、4-8Hz、2-4Hz这些频率范围。而小波分解后不同层的细节系数对应着不同的频率范围，第4层至第6层细节系数（D4-D6）正好对应着这些频率范围。因此，我们分别重构第4层至第6层的细节系数，以突出QRS波群的特征。

        其中，di​ 表示第i层重构后的细节系数；c 和 l 是小波分解得到的系数和长度向量；wname 为小波基函数名称，这里同样选用db8小波；i 为重构的层号，这里分别取4、5、6层。

        

2.4 动态权重融合

        为了进一步融合多尺度特征，我们计算各重构层的能量占比。能量占比反映了每一层细节系数在整体信号中的能量贡献。具体来说，计算各层细节系数的平方和占总平方和的比例。能量占比的计算公式为：

        其中，αi​ 表示第i层细节系数的能量占比；di​ 表示第i层重构后的细节系数。

        基于能量占比，我们对各层细节系数的绝对值进行加权融合，生成综合特征信号。这样可以突出能量占比高的层的特征，使得综合特征信号更准确地反映QRS波群的特征。

        综合特征信号的生成公式为：

        其中，Scombined​(t) 表示综合特征信号；αi​ 表示第i层细节系数的能量占比；di​(t) 表示第i层重构后的细节系数在时间t处的值。

图3：特征信号生成结果

2.5 动态阈值生成与峰值检测

        为了检测R波峰值，对综合特征信号进行峰值检测。采用动态阈值策略以适应信号的时变特性。动态阈值根据信号的局部统计特性（如噪声水平和信号幅度）进行调整。具体来说，在滑动窗口内估计噪声水平和信号幅度，动态生成阈值：

        其中，噪声水平基于稳健中位数法估计，信号幅度取窗口内最大值。

        在综合特征信号中检测高于阈值的峰值，结合心电生理约束（如最小峰值间距对应300ms）筛选候选R峰。通过与真实注释对比验证，补偿相位延迟并剔除边缘误检，最终确定R波位置。

        小波熵阈值法在多个方面表现出显著优势。首先，它通过多尺度特征融合，能够更全面地捕捉QRS波群的特征信息，提高检测的准确性。其次，动态阈值策略能够适应信号的时变特性，确保在不同噪声环境下都能可靠地检测到R波。此外，该方法对噪声具有较强的鲁棒性，能够在低信噪比条件下保持较高的检测性能。虽然其计算复杂度略高于简单时域或频域方法，但通过优化算法，可以在实际应用中实现高效的实时检测。

图4：小波熵阈值法R峰检测结果

5. 性能评估与对比分析

5.1 性能指标计算

        采用灵敏度（Sensitivity, Sen）、特异性（Specificity, Spe）、阳性预测率（Positive Predictive Value, PPV）、准确率（Accuracy, Acc）评估检测性能：

• 灵敏度（Sensitivity, Sen）   

        灵敏度是指模型正确识别出的正例占所有实际正例的比例。用于评估模型对实际正例的识别能力。

• 特异性（Specificity, Spe）

        特异性是指模型正确识别出的负例占所有实际负例的比例。用于评估模型对实际负例的识别能力。

• 阳性预测率（Positive Predictive Value, PPV）

        阳性预测率是指模型检测到的正例中实际为正例的比例。用于评估模型检测结果的可靠性。

• 准确率（Accuracy, Acc）

        准确率是指模型正确识别的样本数占总样本数的比例。用于评估模型整体的识别正确率。

5.2 对比方法

与传统时域、频域及时域、频域相结合的ECG检测方法对比：

• 时域分析法：基于一阶差分突出跳变特征，检测差分信号峰值。

        时域分析法主要基于ECG信号在时间轴上的波形特征。它通过计算信号的一阶差分来突出信号中的突变部分，这些突变通常对应着ECG信号中的关键特征点，如R波的峰值。一阶差分可以看作是一种简单的高通滤波器，它增强了信号中的高频成分，这些高频成分往往与ECG信号中的尖锐变化相关。

        一阶差分的计算公式为：

df(n)=x(n)−x(n−1)

        其中，x(n) 表示原始 ECG 信号在时间点 n 处的幅值，df(n) 为差分后的信号。对于 ECG 信号而言，R 波是心脏电活动变化最为剧烈的部分，在原始信号中表现为幅值的显著跳变。经一阶差分后，这种跳变会被进一步放大，使得 R 波位置在差分信号上呈现出明显的峰值。在实际检测中，首先对原始 ECG 信号进行逐点差分运算，得到差分信号序列。然后，对差分信号进行平滑处理以减少噪声干扰，通常采用移动平均或高斯滤波等方法。接着，对平滑后的差分信号进行归一化，使其幅值范围适应后续的检测算法。最后，在设定的时间窗口内搜索差分信号的局部最大值，依据预设的幅值阈值和时间间隔阈值，判定 R 波的位置。若差分信号的峰值超过幅值阈值，且相邻峰值之间的时间间隔大于设定的最小心搏间隔，则认为检测到一个 R 波。

• 频域分析法：利用FFT识别QRS频段，检测滤波后信号峰值。

        频域分析法主要基于ECG信号在频域上的特征分布。通过将信号从时域转换到频域，可以更清晰地分析信号的频率成分。QRS波群在频域上具有特定的频段分布，通常集中在10-20Hz左右。利用频域分析可以有效滤除噪声和其他干扰成分，突出QRS波群的特征。

        快速傅里叶变换（FFT）将时域信号转换为频域信号，其公式为：

        其中，x[n] 是时域信号，X[k] 是频域信号，N 是信号的长度。

        逆快速傅里叶变换（IFFT）将频域信号转换回时域信号，其公式为：

        频域分析法首先对原始ECG信号进行预处理，包括带通滤波以去除高频噪声和低频漂移。随后，利用FFT将滤波后的信号转换到频域，分析频谱以识别QRS波群对应的频段。为了检测R波峰值，对滤波后的时域信号进行峰值检测，设置一个动态阈值以区分有效信号和噪声。检测到的峰值位置即为R波的候选位置，随后根据心电生理的先验知识进行筛选，以去除伪峰值。

• 小波多尺度法：重构特定频段细节系数并直接检测。

        小波多尺度法利用小波变换的多分辨率特性，将信号分解为不同尺度下的近似系数和细节系数。不同尺度对应着信号的不同频率成分，通过选择特定的尺度可以突出不同频率范围内的信号特征。对于ECG信号中的QRS波群，通常可以选择中等尺度的细节系数进行分析，这些系数包含了QRS波群的特征信息。

        小波分解公式为：

        其中，cAj​[k] 是第j层的近似系数，cDj​[k] 是第j层的细节系数，ϕj,k​(n) 是尺度函数，ψj,k​(n) 是小波函数。

        小波重构公式为：

        小波多尺度法首先对原始ECG信号进行预处理，以去除噪声。随后，利用小波变换将信号分解为多个尺度的近似系数和细节系数。选择与QRS波群频率范围对应的尺度的细节系数进行重构，得到突出QRS波群特征的信号。为了检测R波峰值，对重构后的信号进行峰值检测，设置一个动态阈值以区分有效信号和噪声。检测到的峰值位置即为R波的候选位置，随后根据心电生理的先验知识进行筛选，以去除伪峰值。

• 小波熵阈值法：通过能量加权融合多尺度特征，结合动态阈值检测。

5.3 结果与讨论

        本实验选取MIT-BIH心律失常数据库中的101号记录，650000个采样点，采样频率为360Hz。

（1）不同方法的R峰-峰值检测结果

        为方便观察，分别选取6500和650000个采样点，基于四种方法绘制图像，结果如下所示。

图5：不同方法的R峰-峰值检测结果（6500个采样点）

图6：不同方法的RR间期序列（6500个采样点）

图7：不同方法的R峰-峰值检测结果（650000个采样点）

图8：不同方法的RR间期序列（650000个采样点）

        

  对比原始数据的注释文件中R波的数量与个算法的性能指标，对比情况如下表所示。

表1：不同算法的R峰检测数量

算法	检测到R峰数量	注释文件-R峰数量
小波熵阈值法	1867	1874
时域分析法	1404	1874
频域分析法	1864	1874
小波多尺度法	1867	1874

表2：不同算法的R峰检测百分比

方法	检测的百分比 (%)
小波熵阈值法	99.6265
时域分析法	74.92
频域分析法	99.4664
小波多尺度法	99.6265

表3：不同算法的平均心率对比

方法	平均心率(bpm)
原始数据	61.8817
小波熵阈值法	62.1
时域分析法	55.4
频域分析法	62.0
小波多尺度法	62.1

        简要分析：从上图5和图7可以看到，小波熵阈值法和频域分析法的R波检测效果目测较好；小波多尺度法的检测效果一般，存在很多误检的情况；时域分析法的检测效果较差，大部分都错检。从表1可知，小波熵阈值法和小波多尺度法，都尽可能的检测到了R波的数量；频域分析法次之；而时域分析法检测到的R波数目最少。

        造成上述结果的可能原因分析如下：

        小波熵阈值法结合了小波变换的多分辨率特性和信息熵理论，能够动态地为每个尺度分配权重，从而实现多尺度特征的融合。这种融合方式可以更全面地捕捉QRS波群的特征信息，同时抑制噪声干扰。此外，该方法采用自适应动态阈值策略，能够根据信号的局部统计特性调整阈值，减少因噪声引起的误检和漏检。因此，小波熵阈值法能够尽可能地检测到更多的R波，且误检率较低。

        频域分析法通过带通滤波（0.5-45 Hz）有效去除了高频噪声和低频漂移，保留了QRS波群的主要频率成分。利用FFT将信号转换到频域后，能够更清晰地识别QRS波群对应的频段（10-20 Hz），并通过滤波和阈值处理突出这些频段的特征。因此，频域分析法能够较为准确地检测到R波，检测效果较好，但相较于基于小波变换的方法，其对复杂噪声的适应性稍弱，导致检测到的R波数量略少于小波熵阈值法和小波多尺度法。

        小波多尺度法重构了特定频段的细节系数并直接检测，虽然能够突出QRS波群的特征，但可能未充分考虑到不同尺度特征的能量分布和贡献，导致融合后的特征信号未能最大限度地突出QRS波群。此外，该方法在阈值生成和峰值检测的参数设置上可能不够优化，无法有效区分真实R波和噪声引起的伪峰值，从而出现较多误检。

        时域分析法仅基于一阶差分信号进行检测，对噪声较为敏感。ECG信号中的噪声（如肌电干扰、基线漂移等）可能会导致差分信号中出现大量伪峰值，增加误检率。此外，该方法仅利用了一阶差分突出跳变特征，未能充分挖掘ECG信号在其他时域或频域的特征，导致对R波的特征描述不够全面和准确。同时，时域分析法中的峰值检测参数可能较难优化，难以适应不同噪声条件和个体差异下的ECG信号，从而导致漏检和误检较多，检测到的R波数量最少。

（2）不同方法的RR间期分布对比结果

        四种方法的RR间期分布几乎都集中在800~1100ms范围内，其中时域分析法的RR间期分布散，误差较大。

图9：不同方法的RR间期分布对比（650000个采样点）

（3）不同方法的性能指标对比

表4：各算法性能指标对比

算法	TP	TN	FP	FN	灵敏度(%)	特异性(%)	阳性预测值(%)	准确率(%)
小波熵阈值法	1859	648132	8	1	99.9462	99.9988	99.5715	99.9986
时域分析法	1401	648137	3	459	75.3226	99.9995	99.7863	99.9289
频域分析法	1859	648135	5	1	99.9462	99.9992	99.7318	99.9991
小波多尺度法	1859	648132	8	1	99.9462	99.9988	99.5715	99.9986

        简要分析：

        小波熵阈值法在本次实验中表现优异， TP（真实阳性）达到1859， FP（假阳性）和 FN（假阴性）分别仅为8和1，这使其在灵敏度（99.9462%）、特异性（99.9988%）、阳性预测值（99.5715%）和准确率（99.9986%）上均表现突出。小波熵阈值法通过小波分析与信息熵理论相结合，能够有效突出ECG信号中的关键特征成分，同时抑制噪声干扰，实现精准检测。

        时域分析法的表现相对较差，TP为1401， FP仅为3，但 FN高达459，导致灵敏度（75.3226%）显著低于其他方法。该方法仅能通过一阶差分检测跳变特征，易受噪声干扰，致使大量R波未被检测。

        频域分析法的TP为1859， FN仅为1，灵敏度（99.9462%）与小波熵阈值法相当。但其FP稍高为5，特异性（99.9992%）略低于小波熵阈值法，准确率为99.9991%。该方法通过FFT转换识别QRS频段，能有效滤除特定频率噪声，但对非平稳信号适应性不佳，可能引发误检。

        小波多尺度法的TP为1859， FP和 FN均为8和1，灵敏度（99.9462%）与小波熵阈值法相同。特异性（99.9988%）和准确率（99.9986%）略低于小波熵阈值法。该方法重构特定频段细节系数直接检测，但未能充分融合多尺度特征，且阈值处理不够精细，影响了检测效果。

        综合分析：

• 小波熵阈值法和小波多尺度法在灵敏度、特异性、阳性预测值和准确率上均表现最佳，适用于高精度ECG信号分析。但是小波多尺度法检测的R波存在误检情况。

• 频域分析法在灵敏度和特异性方面表现良好，但在准确性上略逊于小波熵阈值法和小波多尺度法，适合对假阳性有一定容忍度的场景。但是频域分析法检测的R波存在漏检情况。

• 时域分析法整体性能较差，灵敏度低且漏检、错检严重。

        总体来看，小波熵阈值法、小波多尺度法和频域分析法在检测R峰方面具有较高的灵敏度和准确率，适合需要高检测精度的应用场景；而时域分析法尽管特异性和阳性预测值略高，但由于灵敏度较低，可能会漏掉较多的R峰，适用于对假阳性控制严格且能够接受一定漏检的情况。

Tips：下一讲，我们将进一步探讨，心电信号处理与应用的其他内容。

以上就是基于小波熵阈值的R峰检测（与时域-频域-多尺度小波法对比）的全部内容啦~

我们下期再见，拜拜(⭐v⭐) ~

（Ps：有代码实现需求，请见主页信息，谢谢支持！~）