高斯函数（Gaussian Function）

高斯函数定义

高斯函数（Gaussian Function）是一种以钟形曲线为图形的平滑函数，形式为：

μ：均值，决定曲线的中心位置；
σ：标准差，决定曲线的宽度（扩散程度）；
这个函数最大值为 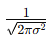，当 x=μ 时取得最大值；

高斯函数图像

数学特性

图像特点：中间高、两边低，左右对称，即“钟形曲线”。

特性	描述
平滑性	高斯函数处处可导，变化平稳，不突变，适合做连续评分
有界性	函数值始终在 $(0,\frac{1}{\sqrt{2\pi {\sigma }^2}}]$，不会无限大或小
局部性	离中心（均值）越远，函数值下降越快，对异常值自动抑制
可控性	通过调整 $\mu$、$\sigma$ 可控制中心和影响范围

优势（在参考文献中的作用）

作用	原因
平滑评分结果	对 $\delta$ 的处理是连续、柔和的，不突变
抑制极端值干扰	距离大时 $f(\delta )\to 0$，不会让离群点评分过高
提升鲁棒性	更稳健地区分边缘点与真正的异常点
保留局部性信息	评分集中在合理范围内，适合复杂结构数据

高斯函数用于距离评分中，可以有效平滑距离差异，减少极端值对评分过程的干扰。
采用高斯函数平滑距离评分的文献：Abhaya, Abhaya, 和Bidyut Kr. Patra. 《An Efficient Method for Autoencoder Based Outlier Detection》. Expert Systems with Applications 213 (2023年3月): 118904. https://doi.org/10.1016/j.eswa.2022.118904.