当前位置：首页 > news >正文

25/6/11 ＜算法笔记＞RL基础算法讲解

news 来源：原创 2025/6/15 8:27:51

今天来总结一下AC,A2C,DDPG,HAC,MADDPG,MCTS,PlaNet,PPO,QMIX,SAC算法的各个主要内容和各个算法的优势和适配哪些环境场景。

首先是AC算法，简单来说就是一个执行者和一个评论家，两个互相提升，互相影响，AC算法是后面很多强化学习算法的基础算法，它结合了策略梯度（Policy Gradient） 和值函数逼近（Value Function Approximation） 的优势。

大体流程就是，当前策略和环境交互，得到轨迹 {st,at,rt+1,st+1}，然后Critic用TD误差更新值函数（如Q值或V值），接着Actor用Critic提供的 Q(st,at) 或优势函数 A(st,at) 计算策略梯度，然后更新。适合机器人和游戏等场景。

咱来看下大致代码：

import torch
import torch.nn as nn
import torch.optim as optimclass Actor(nn.Module):def __init__(self,state_dim,action_dim):super().__init__()self.net = nn.Sequential(nn.Linear(state_dim,64),nn.ReLU(),nn.LinearI(64,action_dim),nn.Softmax(dim = -1))def forward(self,state):return self.net(state)class Critic(nn.Module):def __init__(self,state_dim):super().__init__()self.net = nn.Sequential(nn.Linear(state_dim,64),nn.ReLu(),nn.Linear(64,1))def forward(self,state):return self.net(state)class AC_Agent:def __init__(self,state_dim,action_dim,gamma =0.99,lr = 0.001):self.actor = Actor(state_dim,action_dim)self.critic = Critic(state_dim)self.optimizer_actor = optim.Adam(self.actor.parameters(),lr = lr)self.optimizer_critic = optim.Adam(self.critic.parameters(),lr = lr)self.gamma = gamma def select_action(self,state):state = torch.FloatTensor(state)probs = self.actor(state)dist = torch.distributions.Categorical(probs)action = dist.sample()log_prob = dist.log_prob(action)return action.item(),log_probdef update(self,state,log_prob,reward,next_state,done):value = self.critic(torch.FloatTenstor(state))next_value = self.critic(torch.FloatTensor(next_state)) if not done else 0td_target = reward+self.gamma*next_valuetd_error = td_target - valuecritic_loss = td_error.pow(2).mean()self.optimizer_critic.zero_grad()critic_loss.backward()self.optimizer_critic.step()actor_loss = -log_prob*td_error.detach()self.optimizer_actor.zero_grad()actor_loss.backward()self.optimizer_actor.step()

A2C

在AC的基础上引入优势函数， A(s,a)=Q(s,a)−V(s)≈r+γV(s′)−V(s)来衡量动作相对平均水平的优势，进一步降低方差。

import torch
import torch.nn as nn
import torch.optim as optimclass Actor(nn.Module):def __init__(self,state_dim,action_dim):super().__init__()self.net = nn.Sequential(nn.Linear(state_dim,64),nn.ReLu(),nn.Linear(64,action_dim),nn.Softmax(dim=-1))def forward(self,state):return self.net(state)class Critic(nn.Module):def __init__(self, state_dim):super().__init__()self.net = nn.Sequential(nn.Linear(state_dim,64),nn.ReLU(),nn.Linear(64,1))def forward(self,state):return self.net(state)class A2C_Agent:def __init__(self,state_dim,action_dim,gamma = 0.99,lr = 0.001):self.actor = Actor(state_dim,action_dim)self.critic = Critic(state_dim)self.optimizer = optim.Adam(list(self.actor.parameters())+list(self.critic.parameters()),lr = lr)self.gamma = gammadef update(self,states,actions,rewards,next_states,dones):states = torch.FloatTensor(states)rewards = torch.FloatTensor(rewards)dones = torch.FloatTensor(dones)values = self.critic(states).squeeze()next_values = self.critic(torch.FloatTensor(next_states)).squeeze()next_values[dones] = 0############advantages = rewards + self.gamma*next_values -values###############################critic_loss = advantages.pow(2).mean()probs = self.actor(states)dists = torch.distributions.Categorical(probs)#将概率分布转化为离散分布对象log_probs = dists.log_prob(torch.LongTensor(actions))actor_loss = -(log_probs * advantages.detach()).mean()total_loss = actor_loss + 0.5*critic_lossself.optimizer.zero_grad()total_loss.backward()self.optimizer.step()

优势函数为advantages = rewards + self.gamma*next_values -values

它之后作为loss更新网络。

DDPG

DDPG是一种面向连续动作空间的强化学习算法，结合了深度Q网络（DQN） 和策略梯度（Policy Gradient） 方法的优势。

Critic的目标变为了采样小批量样本，计算目标Q值：

最小化Critic的均方误差损失。

Actor的目标：通过梯度上升更新Actor：

优势是能高效处理连续动作。

class Actor(nn.Module):def __init__(self,state_dim,action_dim):super(Actor,self).__init__()self.fc1 = nn.Linear(state_dim,30)self.fc2 = nn.Linear(30,action_dim)self.fc1.weight.data.normal_(0,0.1)#权重初始化self.fc2.weight.data.normal_(0,0.1)def forward(self,state):x = torch.relu(self,fc1(state)),action = torch.tanh(self.fc2(x))*ACTION_BOUND return action class Critic(nn.Module):def __init__(self,state_dim,action_dim):super(Critic,self).__init__()self.fc1 = nn.Linear(state_dim + action_dim,30)self.fc2 = nn.Linear(30,1)self.fc1.weight.data.normal_(0,0.1)self.fc2.weight.data.normal_(0,0.1)def forward(self,state,action):x = torch.cat([state,action],dim = 1)x = torch.relu(self,fc1(x))q_value = self.fc2(x)return q_valueclass ReplayBuffer:def __init__(self,capacity):self.buffer = deque(maxlen = capacity)def push(self,state,action,reward,next_state,done):self.buffer.append((state,action,reward,next_state,done))def sample(self,batch_size):batch = random.sample(self.buffer,batch_size)states,actions,rewards,next_states,dones = zip(*batch)return (torch.FloatTensor(states),torch.FloatTensor(actions),torch.FloatTensor(reward).unsqueeze(1),torch.FloatTensor(next_states),torch.FloatTensor(dones).unsqueeze(1))def __len__(self):return len(self.buffer)class DDPGAgent:def __init__(self,state_dim,action_dim):self.actor = Actor()self.critic = Critic()self.actor_target = Actor()self.critic_target = Critic()self.actor_target.load_state_dict(self.actor.state_dict())self.critic_target.load_state_dict(self.critic.state_dict())self.noise = OUNoise(action_dim)def select_action(self,state,add_noise = True):action = self.actor(state)if add_noise:action+=self.noise.sample()return np.clip(action,-ACTION_BOUND,ACTION_BOUND)def update(self):target_q = rewards + GAMMA*(1-dones)*self.critic_target(next_target,next_actions)critic_loss = nn.MSELoss()(current_q,target_q)actor_loss = -self.critic(states,self.actor(states)).mean()for param,target_param in zip(net.parameters(),target_net.parameters()):target_param.data.copy_(TAU*param.data + (1-TAU)*target_param.data)
class OUNoise:def __init__(self,action_dim,mu=0,theta=0.15,sigma = 0.2):self.state = np.ones(action_dim)*mudef sample(self):dx = self.theta*(self.mu - self.state)+self.sigma*np.random.randn(self.action_dim)self.state += dx return self.stateenv = gym.make('P-v1')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
agent = DDPGAgent(state_dim,action_dim)for episode in range(EPISODES):state = env.reset()total_reward = 0agent.noise.reset()for step in range(EP_STEPS):action = agent.select_action(state,add_noise=True)next_state,reward,done,_=env.step(action)agent.memory.push(state,action,reward,next_state,done)state = next_statetotal_reward += rewardif len(agent.memory)>BATH_SIZE:agent.update()if done:break

HAC

HAC是啥？一句话说清

像公司里领导派活，员工干活！

高层（Manager）：只定目标（比如“拿下市场30%份额”），不碰具体操作。

底层（Worker）：只负责执行（比如“地推100个客户”），不管战略。

一、核心思想

HAC通过分层决策结构解决长时域任务中的稀疏奖励问题：

HAC怎么运作？分三步走

领导画饼：高层看全局（当前状态+终极目标），拆解出子目标（例如“先攻占华东市场”）。

员工冲刺：底层拿到子目标，疯狂执行动作（比如发传单、搞促销），目标就是逼近领导定的KPI。

发奖金原则：

员工：离子目标越近，奖金越多（内在奖励：奖金 = -距离）。

领导：子目标完成后，看整个任务赚了多少钱（环境奖励），再调整策略。

import torch
import torch.nn as nn
import torch.optimizer as optim 
import numpy as np
import gymclass GoalConditionedNetwork(nn.Module):def __init__(self,state_dim,goal_dim,action_dim,hidden_dim=128)super().__init__()self.net = nn.Sequential(nn.Linear(state_dim + goal_dim,hidden_dim),nn.ReLU(),nn.Linear(hidden_dim,hidden_dim),nn.ReLU(),nn.Linear(hidden_dim,action_dim))def forward(self,state,goal):x =torch.cat([state,goal],dim=-1)return self.net(x)
class Critic(nn.Module):def __init__(self,state_dim,goal_dim,action_dim):super().__init__()self.value_net = GoalConditionedNetwork(state_dim,goal_dim,1)def forward(self,state,goal,action):x = torch.cat([state,goal,action],dim=-1)return self.value_net(x,torch.zero_like(goal))
class HACAgent:def __init__(self,env_name,k_level =2 ,subgoal_horizon = 50):self.env = gym.make(env_name)self.k_level = k_levelself.H = subgoal_horizonself.layers =[]for i in range(k_level):if i == 0:actor = Actor(self.env.observation_space.shape[0],self.env.observation_space_shape[0],self.env.action_space.shape[0])critic = Critic(self.env.observation_space.shape[0], self.env.observation_space.shape[0], self.env.action_space.shape[0])else:  # 高层: 输出子目标（视为特殊动作）actor = Actor(self.env.observation_space.shape[0], self.env.observation_space.shape[0], self.env.observation_space.shape[0])critic = Critic(self.env.observation_space.shape[0], self.env.observation_space.shape[0], self.env.observation_space.shape[0])self.layers.append({'actor': actor, 'critic': critic})self.replay_buffers = [ReplayBuffer() for _ in range(k_level)]self.optimizers = []for layer in self.layers:self.optimizers.append({'actor': optim.Adam(layer['actor'].parameters(), lr=1e-4),'critic': optim.Adam(layer['critic'].parameters(), lr=1e-3)})def act(self,state,goal,layer_idx):action = self.layers[layer_idx]['actor'](state,goal)noise = torch.randn_like(action) * 0.1return torch.clamp(action + noise,-1,1)def update(self,layer_idx,batch_size = 64):states, goals, actions, rewards, next_states, dones = self.replay_buffers[layer_idx].sample(batch_size)# Critic更新: 最小化时序差分误差 (TD Loss)with torch.no_grad():target_q = rewards + 0.99 * self.layers[layer_idx]['critic'](next_states, goals, self.act(next_states, goals, layer_idx))current_q = self.layers[layer_idx]['critic'](states, goals, actions)critic_loss = nn.MSELoss()(current_q, target_q)# Actor更新: 最大化Q值 (策略梯度)actor_loss = -self.layers[layer_idx]['critic'](states, goals, self.act(states, goals, layer_idx)).mean()# 反向传播self.optimizers[layer_idx]['critic'].zero_grad()critic_loss.backward()self.optimizers[layer_idx]['critic'].step()self.optimizers[layer_idx]['actor'].zero_grad()actor_loss.backward()self.optimizers[layer_idx]['actor'].step()def train_hierarchy(self, state, final_goal, level):if level == 0: action = self.act(state, final_goal, level)next_state, reward, done, _ = self.env.step(action)return next_state, reward, donesubgoal = self.act(state, final_goal, level)for _ in range(self.H):  next_state, reward, done = self.train_hierarchy(state, subgoal, level-1)if done or self.check_subgoal(state, subgoal): breakstate = next_stateintrinsic_reward = -np.linalg.norm(state - subgoal)return next_state, intrinsic_reward, donedef check_subgoal(self, state, subgoal, threshold=0.05):"""判断是否达成子目标 (欧氏距离)"""return np.linalg.norm(state - subgoal) < threshold
class ReplayBuffer:def __init__(self, capacity=100000):self.buffer = []self.capacity = capacitydef add(self, state, goal, action, reward, next_state, done):"""存储转换样本"""if len(self.buffer) >= self.capacity:self.buffer.pop(0)self.buffer.append((state, goal, action, reward, next_state, done))# HER核心: 用实际状态替换目标生成新样本 [2,6](@ref)self.buffer.append((state, next_state, action, 0, next_state, True))def sample(self, batch_size):indices = np.random.randint(len(self.buffer), size=batch_size)batch = [self.buffer[i] for i in indices]return [torch.tensor(x) for x in zip(*batch)]if __name__ == "__main__":agent = HACAgent("MountainCarContinuous-v0", k_level=2)for episode in range(1000):state = agent.env.reset()final_goal = np.array([0.48, 0.04])  # 山顶目标 [2](@ref)total_reward = 0done = Falsewhile not done:# 从最高层开始执行策略next_state, reward, done = agent.train_hierarchy(state, final_goal, agent.k_level-1)total_reward += rewardstate = next_state# 每10轮更新所有层级if episode % 10 == 0:for level in range(agent.k_level):agent.update(level)print(f"Episode {episode}, Reward: {total_reward:.2f}")

HER

强化学习中的“事后诸葛亮”技术(HER）核心逻辑是：

“既然已经知道结果，不如假装这个结果就是当初的目标，重新学习一遍！”

机器人试图抓取杯子但失败了 → 实际抓到了旁边的笔。

传统方法：判定为失败，丢弃该经验。

HER方法：将目标临时改为“抓到笔”，生成新样本（状态+动作+新目标+成功奖励），让算法学习到“虽然没抓到杯子，但抓笔的动作是有价值的”。

这种“用实际结果重新定义目标”的思维方式，与人类“事后诸葛亮”（事情发生后声称自己早有预料）的行为逻辑高度相似。

MADDPG

多智能体强化学习领域的标志性算法,基于DDPG扩展而来，核心解决多智能体协作与竞争环境中的连续动作空间问题。

DDPG是单兵作战，那MADDPG就是多兵协作，

DDPG的短板：多个智能体独立训练时，环境因其他智能体策略变化而“失控”（如队友突然改变战术，导致你的策略失效）

MADDPG的突破：

Actor 只用局部观察（如球员只看自己周围的画面）(优势：训练时通过全局视角稳定学习，执行时无需通信，适应实时环境)

Critic 输入全局信息：消除环境波动影响（教练用全局数据稳定指导）

策略多样性：训练时为每个智能体准备多套策略（如球员练多种战术），应对对手变化

class MADDPGAgentManager:def __init__(self,num_agent:int,obs_dim_list:List[int],action_dim:int,actor_lr:float,critic_lr:float,gamma:float,tau:float,device:torch.device):self.num_agents = num_agentsself.obs_dim_list = obs_dim_listself.gamma = gammaself.tau = tauself.device = devicejoint_obs_dim = sum(obs_dim_list)joint_action_dim = sum(obs_dim_list)joint_action_dim_one_hot = num_agents*action_dimself.actors:List[ActorDiscrete] = []self.critics:List[CentralizedCritic]=[]self.target_actors:List[ActorDiscrete] = []self.target_critics:List[CentralizedCritic]=[]self.actor_optimizers:List[optim.Optimizer]=[]self.critic_optimizers:List[optim.Optimizer]=[]for i in range(num_agents):actor = ActorDiscrete(obs_dim_list[i], action_dim).to(device)critic = CentralizedCritic(joint_obs_dim, joint_action_dim_one_hot).to(device)target_actor = ActorDiscrete(obs_dim_list[i], action_dim).to(device)target_critic = CentralizedCritic(joint_obs_dim, joint_action_dim_one_hot).to(device)# 初始化目标网络target_actor.load_state_dict(actor.state_dict())target_critic.load_state_dict(critic.state_dict())for p in target_actor.parameters(): p.requires_grad = Falsefor p in target_critic.parameters(): p.requires_grad = False# 创建优化器actor_optimizer = optim.Adam(actor.parameters(), lr=actor_lr)critic_optimizer = optim.Adam(critic.parameters(), lr=critic_lr)self.actors.append(actor)self.critics.append(critic)self.target_actors.append(target_actor)self.target_critics.append(target_critic)self.actor_optimizers.append(actor_optimizer)self.critic_optimizers.append(critic_optimizer)def select_actions(self, obs_list: List[torch.Tensor], use_exploration=True) -> Tuple[List[int], List[torch.Tensor]]:""" 基于它们的局部观测为所有智能体选择动作。 """actions = []log_probs = []for i in range(self.num_agents):self.actors[i].eval()with torch.no_grad():act, log_prob = self.actors[i].select_action(obs_list[i].to(self.device), use_exploration)# 如果是单个观测，转换为标量if act.dim() == 0:act = act.item()self.actors[i].train()actions.append(act)log_probs.append(log_prob)return actions, log_probsdef update(self,batch:Experience,agent_id:int)->Tuple[float,float]:obs_batch,act_batch,rew_batch,next_obs_batch,dones_batch = batchbatch_size = obs_batch.shape[0]joint_obs = obs_batch.view(batch_size,-1).to(self.device)joint_next_obs = next_obs_batch.view(batch_size,-1).to(self.device)act_one_hot = F.one_hot(act_barth,num_classes = self.action_dim).float()joint_actions_one_hot = act_one_hot.view(batch_size,-1).to(self.device)reward_i =rew_batch[:,agent_id].unsequeeze(-1).to(self.device)dones_i = dones_batch[:,agent_id].unsequeeze(-1).to(self.device)with torch.no_grad():target_next_actions_list = []for j in range(self.num_agents):obs_j_next= next_obs_batch[:,j,:].to(device)action_j_next,_ = self.target_actors[j].select_action(obs_j_next,use_exploration=False)acrion_j_next_one_hot = F.one_hot(action_j_next,num_classes = self.action_dim).float()target_next_actions_list.append(action_j_next_one_hot)joint_target_next_actions = torch.cat(target_next_actions_list,dim=1).to(self.device)q_target_next = self.target_critics[agent_id](joint_next_obs, joint_target_next_actions)# 计算目标 y = r_i + gamma * Q'_i * (1 - d_i)y = rewards_i + self.gamma * (1.0 - dones_i) * q_target_nextq_current = self.critics[agent_id](joint_obs, joint_actions_one_hot)# 计算Critic损失critic_loss = F.mse_loss(q_current, y)# 优化Critic iself.critic_optimizers[agent_id].zero_grad()critic_loss.backward()torch.nn.utils.clip_grad_norm_(self.critics[agent_id].parameters(), 1.0)  # 可选裁剪self.critic_optimizers[agent_id].step()for p in self.critics[agent_id].parameters():p.requires_grad = Falsecurrent_actions_list = []log_probs_i_list = []  # 仅存储智能体i的log_probfor j in range(self.num_agents):obs_j = obs_batch[:, j, :].to(self.device)# 更新需要动作概率/对数几率 - 使用Gumbel-Softmax或类似REINFORCE的更新dist_j = self.actors[j](obs_j)  # 获取分类分布# 如果我们使用DDPG目标：Q(s, mu(s))，我们需要确定性动作# 这里我们使用策略梯度适配：最大化 E[log_pi_i * Q_i_detached]action_j = dist_j.sample()  # 采样动作作为Q的输入if j == agent_id:log_prob_i = dist_j.log_prob(action_j)  # 只需要被更新智能体的log_probaction_j_one_hot = F.one_hot(action_j, num_classes=self.action_dim).float()current_actions_list.append(action_j_one_hot)joint_current_actions = torch.cat(current_actions_list, dim=1).to(self.device)# 计算Actor损失: - E[log_pi_i * Q_i_detached]# Q_i使用所有Actor的*当前*动作进行评估q_for_actor_loss = self.critics[agent_id](joint_obs, joint_current_actions)actor_loss = -(log_prob_i * q_for_actor_loss.detach()).mean()  # 分离Q值# 替代的DDPG风格损失（如果Actor是确定性的）：# actor_loss = -self.critics[agent_id](joint_obs, joint_current_actions).mean()# 优化Actor iself.actor_optimizers[agent_id].zero_grad()actor_loss.backward()torch.nn.utils.clip_grad_norm_(self.actors[agent_id].parameters(), 1.0)  # 可选裁剪self.actor_optimizers[agent_id].step()# 解冻Critic梯度for p in self.critics[agent_id].parameters():p.requires_grad = Truereturn critic_loss.item(), actor_loss.item()def update_targets(self) -> None:""" 对所有目标网络执行软更新。 """for i in range(self.num_agents):soft_update(self.target_critics[i], self.critics[i], self.tau)soft_update(self.target_actors[i], self.actors[i], self.tau)

MCTS蒙特卡洛树

MCTS是一种基于随机模拟的启发式搜索算法，用于在复杂决策问题（如棋类游戏、机器人规划）中寻找最优策略。它通过构建一棵动态生长的搜索树，结合随机模拟（蒙特卡洛方法）和树搜索的精确性，平衡探索（未知节点） 与利用（已知高价值节点） 的关系。

MCTS通过迭代执行以下四个步骤构建决策树：

选择（Selection）
- 从根节点（当前状态）出发，递归选择子节点，直到到达一个未完全展开的叶节点。
- 选择策略：使用UCB公式（Upper Confidence Bound） 平衡探索与利用
  ：UCB=NQ+CNlnNparent
- Q：节点累计奖励
- N：节点访问次数
- C：探索常数（通常取 2)
扩展（Expansion）
例如：围棋中从当前棋盘状态生成所有可能的落子位置。
模拟（Simulation）
关键：模拟过程无需依赖领域知识，仅需基础规则。
反向传播（Backpropagation）
- 将模拟结果回传更新路径上所有节点的统计信息：
  - 节点访问次数 N←N+1
  - 累计奖励 Q←Q+奖励值。

MCTS它无需启发式知识：仅依赖游戏规则，适用于规则明确但状态空间庞大的问题（如围棋）。

import math
import numpy as np
import random
from collections import defaultdict# ========== 游戏环境类 ========== [3](@ref)
class TicTacToe:def __init__(self):self.board = np.array([[' ' for _ in range(3)] for _ in range(3)])self.current_player = 'X'self.winner = Nonedef get_available_moves(self):"""返回所有空位坐标"""return [(i, j) for i in range(3) for j in range(3) if self.board[i][j] == ' ']def make_move(self, move):"""执行落子并切换玩家"""i, j = moveif self.board[i][j] != ' ':return Falseself.board[i][j] = self.current_playerif self.check_win():self.winner = self.current_playerelif not self.get_available_moves():self.winner = 'Draw'  # 平局self.current_player = 'O' if self.current_player == 'X' else 'X'return Truedef check_win(self):"""检查胜利条件"""# 检查行和列for i in range(3):if self.board[i][0] == self.board[i][1] == self.board[i][2] != ' ':return Trueif self.board[0][i] == self.board[1][i] == self.board[2][i] != ' ':return True# 检查对角线if self.board[0][0] == self.board[1][1] == self.board[2][2] != ' ':return Trueif self.board[0][2] == self.board[1][1] == self.board[2][0] != ' ':return Truereturn Falsedef copy(self):"""深拷贝当前游戏状态"""new_game = TicTacToe()new_game.board = np.copy(self.board)new_game.current_player = self.current_playernew_game.winner = self.winnerreturn new_game# ========== MCTS节点类 ========== [1,7](@ref)
class Node:def __init__(self, game_state, parent=None):self.game_state = game_state  # TicTacToe对象self.parent = parentself.children = []self.visits = 0self.wins = 0  # 累计奖励值def is_fully_expanded(self):"""检查是否完全扩展"""return len(self.children) == len(self.game_state.get_available_moves())def best_child(self, exploration=1.4):"""UCB公式选择最优子节点"""return max(self.children, key=lambda child: child.wins / (child.visits + 1e-6) + exploration * math.sqrt(math.log(self.visits + 1) / (child.visits + 1e-6)))# ========== MCTS搜索算法 ========== [1,3,7](@ref)
class MCTS:def __init__(self, root_state, iterations=1000):self.root = Node(root_state)self.iterations = iterationsdef search(self):"""执行完整MCTS搜索"""for _ in range(self.iterations):# 1. 选择阶段 (Selection)node = self._select(self.root)# 2. 扩展阶段 (Expansion)if node.game_state.winner is None:node = self._expand(node)# 3. 模拟阶段 (Simulation)reward = self._simulate(node.game_state.copy())# 4. 反向传播 (Backpropagation)self._backpropagate(node, reward)# 返回访问次数最多的动作return max(self.root.children, key=lambda c: c.visits)def _select(self, node):"""递归选择子节点直至叶节点"""while node.children and not node.game_state.winner:if not node.is_fully_expanded():return nodenode = node.best_child()return nodedef _expand(self, node):"""扩展新子节点"""available_moves = node.game_state.get_available_moves()for move in available_moves:if move not in [child.move for child in node.children]:new_state = node.game_state.copy()new_state.make_move(move)child = Node(new_state, parent=node)child.move = move  # 记录导致此状态的动作node.children.append(child)return random.choice(node.children)  # 随机选择新扩展节点def _simulate(self, game_state):"""随机模拟至游戏结束"""while game_state.winner is None:move = random.choice(game_state.get_available_moves())game_state.make_move(move)# 奖励计算：胜+1，平+0.5，负+0if game_state.winner == 'X': return 1elif game_state.winner == 'Draw': return 0.5else: return 0def _backpropagate(self, node, reward):"""更新路径上所有节点统计"""while node:node.visits += 1node.wins += rewardnode = node.parent# ========== 主程序示例 ========== [3](@ref)
if __name__ == "__main__":game = TicTacToe()print("初始棋盘：")print(game.board)while not game.winner:if game.current_player == 'X':  # AI回合mcts = MCTS(game.copy(), iterations=1000)best_node = mcts.search()move = best_node.moveprint(f"AI选择落子位置: {move}")else:  # 玩家回合moves = game.get_available_moves()print(f"可选位置: {moves}")move = tuple(map(int, input("输入落子位置(行列号，如'0 1'): ").split()))game.make_move(move)print(game.board)print(f"游戏结束! 胜者: {game.winner}")

PlaNet

PlaNet 是由 Google Research 提出的 基于模型的强化学习（Model-Based RL）算法，核心目标是通过学习环境的潜在动态模型，直接在紧凑的潜在空间中进行规划，从而显著提升样本效率。

它就像你闭眼打游戏🎮：

编码器：睁眼看到画面，立刻记住关键信息（比如敌人位置）

RNN：闭眼时靠记忆推算"如果按左键，敌人会怎么移动"

预测器：纯靠脑补下一步状态（可能猜错）

解码器：睁眼验证脑补的画面和实际是否一致。

核心原理与技术架构

1. 潜在动态模型（Latent Dynamics Model）

PlaNet 的核心创新是避开高维像素空间的直接预测（如传统视频预测模型），转而学习一个低维潜在状态空间的动力学模型

编码器（Encoder）：将图像观测 ot 压缩为潜在状态 st（捕捉物体位置、速度等抽象特征）
循环状态空间模型（RSSM）它分为确定性路径和随机性路径：
- 确定性路径：在完全已知环境下，通过固定规则计算最优路径，结果唯一且可复现。这里通过 RNN 记忆历史信息（ht=RNN(ht−1,st−1,at−1)）。
- 随机性路径：在部分未知或动态环境下，通过概率模型处理不确定性，生成适应变化的路径。这里是预测潜在状态分布 st∼p(st∣ht)，表达环境不确定性。
- 解码器（Decoder）：从 st 重建观测 ot 并预测奖励 rt

2. 潜在空间规划（Latent Space Planning）

PlaNet 的规划过程完全在潜在状态空间中进行，大幅降低计算开销

编码历史观测：将过去图像序列编码为当前潜在状态 st
交叉熵方法（CEM）：
- 采样大量动作序列 {at,at+1,...,at+H}。
- 用 RSSM 预测未来潜在状态 st+1,...,st+H 和奖励 rt,...,rt+H。
- 选择累积奖励最高的动作序列
执行与重规划：仅执行最优序列的首个动作 at∗，收到新观测后重新规划。

大白话讲解PlaNet 的核心组件

1. 环境模拟器（RSSM 模型）

作用：把游戏画面压缩成“抽象记忆”，并预测下一步画面和奖励。

工作流程：

看见画面 → 用编码器（encoder）压缩成“关键特征” ✅

脑补状态 → 结合动作和记忆，预测下一步状态（分两种）：

确定性状态（如“按左键角色必左移”）→ 用 RNN 记忆

随机状态（如“敌人可能向左或向右”）→ 用概率分布表示 🌟

验证脑补 → 用解码器（decoder）把预测状态还原成画面，对比真实画面有多像 ✅

2. 规划器（CEM 算法）

作用：在模拟器中试错 N 套动作方案，选出得分最高的。

操作步骤：

随机生成 100 套动作（如“左跳→右闪→攻击”）

用模拟器推演每套动作结果 → 计算累计奖励（如：杀敌 +10 分，掉坑 -5 分）

选出得分最高的 20 套方案 → 按它们的动作调整策略（均值+波动范围）

只执行最优方案的第一步 → 之后重新规划（避免翻车）

省时省命：

真实游戏只需玩 100 局，传统方法要 10 万局（效率提升 1000 倍）

高维画面也不怕：

不直接处理像素，用“抽象记忆”做决策（类似人脑记关键特征）

规划稳准狠：

在模拟器中试错安全无代价，还能探索冷门神操作

PlaNet = 游戏存档模拟器 + 战术推演大师

它像军师一样，先在沙盘上排兵布阵，验证可行后再出兵，以最小代价赢下战局

PlaNet适用于连续控制任务。

class RSSM(nn.Module):def __init__(self, state_dim, obs_dim, action_dim, hidden_size=200):# 网络定义self.encoder = nn.Sequential(...)  # 观测 → 潜在状态self.rnn = nn.LSTMCell(...)        # 确定性状态传递self.prior_net = nn.Sequential(...) # 先验状态分布self.decoder = nn.Sequential(...)   # 状态重建观测def forward(self, obs, action, prev_state):# 1. 编码观测 → 后验分布post_params = self.encoder(obs)post_mean, post_std = post_params.chunk(2, dim=-1)s_t_post = Normal(post_mean, torch.exp(post_std)).rsample()# 2. RNN更新确定性状态h_t, c_t = self.rnn(torch.cat([action, s_t_post], -1), prev_state)# 3. 预测先验分布prior_params = self.prior_net(h_t)prior_mean, prior_std = prior_params.chunk(2, dim=-1)# 4. 重建观测obs_recon = self.decoder(s_t_post)return (h_t, c_t), (post_mean, post_std), (prior_mean, prior_std), obs_recon
class CEMPlanner:def plan(self,model,initial_state):for _ in range(n_iter):actions= Normal(self.mean,self.std ).sample((n_samples,))rewards= []for a_seq in actions:state = initial_statetotal_reward = 0for t in range(horizon):next_state,reward = model.step(state,a_seq[t])total_reward += rewardstate = next_staterewards.append(total_reward)top_idx = torch.topk(rewards,top_k).indicestop_actions = actions[top_idx]self.mean = top_actionsself.std = top_actions.std(dim = 0)return self.mean[0]def train_planet(env,epochs = 1000):model = RSSM(state_dim= 32,...)planner = CEMPlanner(env.action_dim)for epoch in range(epochs):obs = env.reset()state = model.initial_state()  # 初始化状态for t in range(100):  # 环境交互步数# 规划生成动作action = planner.plan(model, state)# 环境执行next_obs, reward, done = env.step(action)# 模型更新optimizer.zero_grad()state, post, prior, recon = model(next_obs, action, state)loss = elbo_loss(next_obs, recon, post, prior)loss.backward()optimizer.step()

PPO

PPO算法是结合AC架构和策略梯度，优势函数，策略探索，截断机制（招牌）。

这是它的截断机制，目的是为了防止策略更新幅度过大 ，避免策略崩溃。

PPO的创新解决方案：

1.信任区域约束（Trust Region）：通过KL散度限制更新幅度 → 保障训练稳定性

2.重要性采样（Importance Sampling）：用旧策略的数据评估新策略 → 数据重用

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Normal
import gym
import numpy as np# 超参数配置
class Config:def __init__(self):self.env_name = "Pendulum-v1"self.hidden_dim = 256self.actor_lr = 3e-4self.critic_lr = 1e-3self.gamma = 0.99        # 折扣因子self.gae_lambda = 0.95   # GAE参数self.eps_clip = 0.2      # 剪切范围self.K_epochs = 10       # 策略更新轮次self.entropy_coef = 0.01 # 熵正则系数self.batch_size = 64self.buffer_size = 2048# 策略网络（Actor）：输出动作分布参数
class PolicyNet(nn.Module):def __init__(self, state_dim, action_dim, hidden_dim):super().__init__()self.shared = nn.Sequential(nn.Linear(state_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, hidden_dim),nn.ReLU())self.mu_head = nn.Linear(hidden_dim, action_dim)  # 均值输出self.log_std_head = nn.Linear(hidden_dim, action_dim)  # 对数标准差输出def forward(self, state):x = self.shared(state)mu = self.mu_head(x)log_std = self.log_std_head(x)std = torch.exp(log_std).clamp(min=1e-6)  # 确保标准差>0return mu, std# 价值网络（Critic）：评估状态价值
class ValueNet(nn.Module):def __init__(self, state_dim, hidden_dim):super().__init__()self.net = nn.Sequential(nn.Linear(state_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, 1))def forward(self, state):return self.net(state).squeeze(-1)# PPO核心算法类
class PPO:def __init__(self, cfg):self.env = gym.make(cfg.env_name)state_dim = self.env.observation_space.shape[0]action_dim = self.env.action_space.shape[0]self.actor = PolicyNet(state_dim, action_dim, cfg.hidden_dim)self.critic = ValueNet(state_dim, cfg.hidden_dim)self.old_actor = PolicyNet(state_dim, action_dim, cfg.hidden_dim)  # 旧策略self.old_actor.load_state_dict(self.actor.state_dict())self.optimizer = optim.Adam([{'params': self.actor.parameters(), 'lr': cfg.actor_lr},{'params': self.critic.parameters(), 'lr': cfg.critic_lr}])self.cfg = cfgself.buffer = []  # 经验缓冲区def select_action(self, state):state = torch.FloatTensor(state).unsqueeze(0)with torch.no_grad():mu, std = self.old_actor(state)dist = Normal(mu, std)action = dist.sample()log_prob = dist.log_prob(action).sum(-1)  # 多维动作对数概率求和return action.squeeze(0).numpy(), log_prob.item()def compute_gae(self, rewards, values, next_values, dones):"""广义优势估计(GAE)"""deltas = rewards + self.cfg.gamma * next_values * (1 - dones) - valuesadvantages = np.zeros_like(rewards)advantage = 0for t in reversed(range(len(rewards))):advantage = deltas[t] + self.cfg.gamma * self.cfg.gae_lambda * (1 - dones[t]) * advantageadvantages[t] = advantagereturns = advantages + valuesreturn advantages, returnsdef update(self):# 数据转换为张量states = torch.FloatTensor(np.array([t[0] for t in self.buffer]))actions = torch.FloatTensor(np.array([t[1] for t in self.buffer]))old_log_probs = torch.FloatTensor(np.array([t[2] for t in self.buffer]))rewards = torch.FloatTensor(np.array([t[3] for t in self.buffer]))next_states = torch.FloatTensor(np.array([t[4] for t in self.buffer]))dones = torch.FloatTensor(np.array([t[5] for t in self.buffer]))# 计算GAE优势函数with torch.no_grad():values = self.critic(states).numpy()next_values = self.critic(next_states).numpy()advantages, returns = self.compute_gae(rewards.numpy(), values, next_values, dones.numpy())advantages = torch.FloatTensor(advantages)returns = torch.FloatTensor(returns)# 多轮策略优化for _ in range(self.cfg.K_epochs):# 计算新策略的动作概率mu, std = self.actor(states)dist = Normal(mu, std)log_probs = dist.log_prob(actions).sum(-1)# 核心1：概率比计算ratios = torch.exp(log_probs - old_log_probs.detach())# 核心2：Clipped Surrogate Losssurr1 = ratios * advantagessurr2 = torch.clamp(ratios, 1-self.cfg.eps_clip, 1+self.cfg.eps_clip) * advantagesactor_loss = -torch.min(surr1, surr2).mean()# Critic损失（值函数拟合）values_pred = self.critic(states)critic_loss = F.mse_loss(values_pred, returns)# 熵正则项（鼓励探索）entropy = dist.entropy().mean()# 总损失loss = actor_loss + 0.5 * critic_loss - self.cfg.entropy_coef * entropy# 梯度更新self.optimizer.zero_grad()loss.backward()torch.nn.utils.clip_grad_norm_(self.actor.parameters(), 0.5)  # 梯度裁剪torch.nn.utils.clip_grad_norm_(self.critic.parameters(), 0.5)self.optimizer.step()# 更新旧策略self.old_actor.load_state_dict(self.actor.state_dict())self.buffer.clear()def train(self, max_episodes=1000):for ep in range(max_episodes):state, _ = self.env.reset()ep_reward = 0for _ in range(self.cfg.buffer_size):action, log_prob = self.select_action(state)next_state, reward, done, _, _ = self.env.step(action)# 存储经验self.buffer.append((state, action, log_prob, reward, next_state, done))state = next_stateep_reward += rewardif len(self.buffer) == self.cfg.buffer_size:self.update()if done:breakprint(f"Episode {ep+1}, Reward: {ep_reward:.1f}")if __name__ == "__main__":cfg = Config()agent = PPO(cfg)agent.train()

QMXI

集中训练，分散执行

我们先来介绍一下它的三大组件：

智能体网络：每个智能体拥有独立网络，输入为局部观测 ota 和上一步动作 ut−1a，输出当前动作价值 Qa(τa,ua)。

混合网络：功能是将各智能体的 Qa 值融合为全局 Qtot。

超网络：功能是生成混合网络的权重参数。

大白话讲解：QMIX 的目标：让球员训练时参考教练的全局战术（集中训练），比赛时自己快速决策（分散执行）。

QMIX 的运作原理（三步走）：

每人有个“小脑”（Agent Network）

每个智能体用自己的 RNN 网络（如 GRU）分析局部观测（如“对手位置+自己动作”），计算每个动作的收益估值（Q 值）
好比球员根据眼前情况，判断“传球还是投篮更有利”。

2️⃣ 教练的“战术板”（Mixing Network）

教练（混合网络）收集所有球员的 Q 值，结合全场局势（全局状态），用非线性方式融合成团队总收益（Q_tot）
关键设计：
- 融合必须满足单调性——任何球员的 Q 值增加，团队 Q_tot 一定不减少（避免“个人优秀却拖累团队”）；
- 融合权重由“超网络”动态生成，根据战况调整策略
好比教练根据球员能力 + 比分情况，制定“最优战术组合”。

3️⃣ 训练与执行的分离

训练阶段：教练用全局信息（如全场录像）优化战术板，反向更新每个球员的小脑
执行阶段：球员仅凭局部观测独立决策，无需实时问教练
好比训练时看录像分析，比赛时球员自主发挥。

用于多无人机协同作战，智能交通调度，游戏AI.

class QMixAgent(nn.Module):def __init__(self,obs_dim,action_dim,hidden_dim = 64):super().__init__()self.rnn = nn.GRUCell(obs_dim,hidden_dim)self.fc = nn.Sequential(nn.Linear(hidden_dim,hidden_dim),nn.ReLU(),nn.Linear(hidden_dim,action_dim))def forward(self,obs,hidden_state):hidden  =self.rnn(obs,hidden_state)q_value= self.fc(hidden)return q_value,hiddenclass QMixer(nn.Module):def __init__(self,num_agent,state_dim,hidden_dim = 64):super().__init__()self.hyper_w1 = nn.Linear(state_dim,hidden_dim*num_agents)self.hyper_b1 = nn.Linear(state_dim,hidden_dim)self.hyper_w2 = nn.Linear(state_dim,hidden_dim)self.hyper_b2 = nn.Linear(state_dim,1)def forward(self,agent_qs,globals_state):w1 = torch.abs(self.hyper_w2(global_state))b1 = self.hyper_b1(global_state)w2 =torch.abs(self.hyper_w2(global_state))b2 = self.hyper_b2(global_state)agent_qs = agent_qs.view(-1, agent_qs.size(-1))  # 展平智能体维度hidden = torch.bmm(agent_qs.unsqueeze(1), w1.view(-1, agent_qs.size(-1), w1.size(-1)))hidden = torch.relu(hidden + b1.view(-1, 1, -1))hidden = torch.bmm(hidden, w2.view(-1, hidden.size(-1), w2.size(-1)))mixed = hidden + b2.view(-1, 1, -1)# 恢复智能体维度return mixed.view(-1, agent_qs.size(1))
class QMix:def __init__(self, num_agents, obs_dim, action_dim, hidden_dim=64):# 智能体网络（每个智能体独立）self.agents = nn.ModuleList([QMixAgent(obs_dim, action_dim, hidden_dim) for _ in range(num_agents)])# 混合网络self.mixer = QMixer(num_agents, obs_dim, hidden_dim)# 目标网络（稳定训练）self.target_agents = nn.ModuleList([nn.Sequential(agent) for agent in self.agents])self.target_mixer = nn.Sequential(self.mixer)# 初始化目标网络参数for target, source in zip(self.target_agents.parameters(), self.agents.parameters()):target.data.copy_(source.data)for target, source in zip(self.target_mixer.parameters(), self.mixer.parameters()):target.data.copy_(source.data)def select_actions(self, obs_n, hidden_states_n, epsilon=0.1):"""分散执行：根据局部观测选择动作"""q_values = []for i, agent in enumerate(self.agents):q, hidden = agent(obs_n[i], hidden_states_n[i])q_values.append(q)q_values = torch.stack(q_values, dim=1)  # [batch, num_agents, action_dim]# ε-贪婪策略选择动作if np.random.rand() < epsilon:actions = [torch.multinomial(torch.softmax(q, dim=-1), 1).item() for q in q_values]else:actions = [q.argmax(dim=-1).item() for q in q_values]return actions, hidden_states_n# 超参数num_agents = 2obs_dim = 4action_dim = 3hidden_dim = 64gamma = 0.99lr = 0.001batch_size = 32buffer_size = 10000# 初始化环境和智能体env = MultiAgentGridEnv_QMIX(num_agents=num_agents)  # 假设已定义环境agent = QMix(num_agents, obs_dim, action_dim, hidden_dim)# 经验回放池Buffer = namedtuple('Buffer', ['obs_n', 'actions', 'rewards', 'next_obs_n', 'dones'])buffer = deque(maxlen=buffer_size)# 训练循环for episode in range(1000):obs_n = env.reset()hidden_states_n = [torch.zeros(1, hidden_dim) for _ in range(num_agents)]total_reward = 0while True:# 选择动作actions, hidden_states_n = agent.select_actions(obs_n, hidden_states_n)# 执行动作next_obs_n, rewards, dones, _ = env.step(actions)total_reward += sum(rewards)# 存储经验buffer.append((obs_n, actions, rewards, next_obs_n, dones))# 更新网络if len(buffer) >= batch_size:batch = np.array(buffer)[np.random.choice(len(buffer), batch_size)]# 转换为张量obs_batch = torch.FloatTensor(np.array([b[0](@ref)for b in batch]))action_batch = torch.LongTensor(np.array([b[1](@ref)for b in batch]))reward_batch = torch.FloatTensor(np.array([b[2](@ref)for b in batch]))next_obs_batch = torch.FloatTensor(np.array([b[3](@ref)for b in batch]))done_batch = torch.FloatTensor(np.array([b[4](@ref)for b in batch]))# 计算目标 Q 值with torch.no_grad():# 目标网络生成下一状态 Q 值next_q = []for i in range(num_agents):q, _ = agent.target_agents[i](next_obs_batch[:, i](@ref), hidden_states_n[i](@ref))next_q.append(q)next_q = torch.stack(next_q, dim=1)# 混合网络计算全局目标 Q 值target_q = agent.target_mixer(next_q, next_obs_batch)# TD 目标target_q = reward_batch + gamma * (1 - done_batch) * target_q# 计算当前 Q 值current_q = []for i in range(num_agents):q, _ = agent.agents[i](obs_batch[:, i](@ref), hidden_states_n[i](@ref))current_q.append(q)current_q = torch.stack(current_q, dim=1)# 混合网络计算当前全局 Q 值pred_q = agent.mixer(current_q, obs_batch)# 计算损失loss = nn.MSELoss()(pred_q, target_q)# 反向传播agent.optimizer.zero_grad()loss.backward()agent.optimizer.step()# 软更新目标网络for target, source in zip(agent.target_agents.parameters(), agent.agents.parameters()):target.data.copy_(0.995 * target.data + 0.005 * source.data)for target, source in zip(agent.target_mixer.parameters(), agent.mixer.parameters()):target.data.copy_(0.995 * target.data + 0.005 * source.data)obs_n = next_obs_nif all(dones):break

SAC

SAC的独特之处在于引入“最大熵"

SAC的优化目标包含两部分：

累积奖励 + 策略熵：

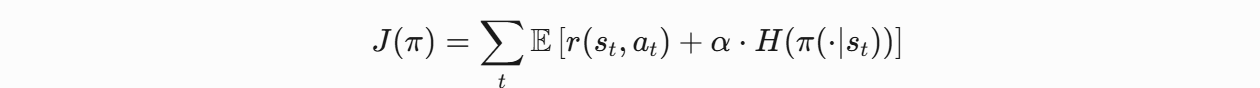
H(π) 是策略熵，衡量动作随机性（熵越高，探索性越强）
α 是熵权重系数，自动调节探索强度

网络架构：双Q网络 + 策略网络

它的critic网络是两个独立的Q网络，分别估计动作价值Q1,Q2.

关键技术:

自动熵调节（Auto-α）：
α 并非固定值，而是根据策略实际熵与目标熵的差异动态调整：

若策略过于确定（熵低）→ 增大 α，鼓励探索；
若策略过于随机（熵高）→ 减小 α，侧重利用

适用于机器人控制和自动驾驶

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
from collections import deque
import randomclass ReplayBuffer:def __init__(self,capacity):self.buffer = deque(maxlen = capacity)def push(self,state,action,reward,next_state,done):self.buffer.append((state,action,reward,next_state,done))def sample(self,batch_size):state,action,reward,next_state,done = zip(*random.sample(self.buffer,batch_size))return np.stack(state),np.stack(action),np.stack(reward),np.stack(next_state),np.stack(done)def __len__(self):return len(self.buffer)class GaussianPolicy(nn.Module):def __init__(self, state_dim, action_dim, hidden_dim=256):super().__init__()self.fc1 = nn.Linear(state_dim, hidden_dim)self.fc2 = nn.Linear(hidden_dim, hidden_dim)self.mean = nn.Linear(hidden_dim, action_dim)self.log_std = nn.Linear(hidden_dim, action_dim)def forward(self, state):x = F.relu(self.fc1(state))x = F.relu(self.fc2(x))mean = self.mean(x)log_std = self.log_std(x)log_std = torch.clamp(log_std, min=-20, max=2)  # 限制log_std范围return mean, log_stddef sample(self, state):# 重参数化采样 (公式11)mean, log_std = self.forward(state)std = log_std.exp()normal = torch.distributions.Normal(mean, std)# 从正态分布采样x_t = normal.rsample()# Tanh变换处理动作边界 (附录C)action = torch.tanh(x_t)# 计算log概率 (公式21)log_prob = normal.log_prob(x_t)log_prob -= torch.log(1 - action.pow(2) + 1e-6)log_prob = log_prob.sum(1, keepdim=True)return action, log_probclass QNetwork(nn.Module):def __init__(self,state_dim,action_dim,hidden_dim=256):super().__init__()self.net = nn.Sequential(nn.Linear(state_dim+action_dim,hidden_dim),nn.ReLU(),nn.Linear(hidden_dim,hidden_dim),nn.ReLU(),nn.Linear(hidden_dim,1))def forward(self,state,action):x = torch.cat([state,action],dim = 1)return self.net(x)class SAC:def __init__(self,state_dim,action_dim,gamma = 0.99,tau=0.005,alpha=0.2,lr=3e-4):self.gamma = gammaself.tau= tauself.alpha = alphaself.policy = GaussianPolicy(state_dim,action_dim)self.policy_optimizer = optim.Adam(self.policy.parameters(),lr=lr)self.q_net1 = QNetwork(state_dim,action_dim)self.q_net2 = QNetwork(state_dim,action_dim)self.target_q_net1.load_state_dict(self.q_net1.state_dict())self.target_q_net2.load_state_dict(self.q_net2.state_dict())self.target_entropy = -action_dimself.log_alpha = torch.tensor(np.log(alpha),requires_grad = True)self.alpha_optimizer = optim.Adam([self.log_alpha],lr=lr)self.replay_buffer =ReplayBuffer(capacity=1000000)def update(self,batch_size):state,action,reward,next_state,done = self.replay_buffer.sample(batch_size)state = torch.FloatTensor(state)action = torch.FloatTensor(action)reward = torch.FloatTensor(reward).unsqueeze(1)next_state =torch.FloatTensor(next_state)done = torch.FloatTensor(done).unsqueeze(1)with torch.no_grad():next_action,next_log_prob = self.policy.sample(next_action)target_q1 = self.target_q_net1(next_state,next_action)target_q2 = self.target_q_net2(next_state,next_action)target_q = torch.min(target_q1,target_q2) - self.alpha*next_log_probtarget_value = reward + (1-done)*self.gamma*target_q    current_q1 = self.q_net1(state, action)current_q2 = self.q_net2(state, action)q_loss1 = F.mse_loss(current_q1, target_value)q_loss2 = F.mse_loss(current_q2, target_value)self.q_optimizer1.zero_grad()q_loss1.backward()self.q_optimizer1.step()self.q_optimizer2.zero_grad()q_loss2.backward()self.q_optimizer2.step()for param in self.q_net1.parameters():param.requires_grad = Falsefor param in self.q_net2.parameters():param.requires_grad = False# 采样新动作new_action, log_prob = self.policy.sample(state)min_q = torch.min(self.q_net1(state, new_action),self.q_net2(state, new_action))policy_loss = (self.alpha * log_prob - min_q).mean()# 优化策略网络self.policy_optimizer.zero_grad()policy_loss.backward()self.policy_optimizer.step()for param in self.q_net1.parameters():param.requires_grad = Truefor param in self.q_net2.parameters():param.requires_grad = Truealpha_loss = -(self.log_alpha * (log_prob + self.target_entropy).detach()).mean()self.alpha_optimizer.zero_grad()alpha_loss.backward()self.alpha_optimizer.step()self.alpha = self.log_alpha.exp()self.soft_update(self.target_q_net1, self.q_net1)self.soft_update(self.target_q_net2, self.q_net2)return q_loss1.item(), q_loss2.item(), policy_loss.item(), alpha_loss.item()def soft_update(self, target, source):"""指数移动平均更新目标网络 (算法1)"""for target_param, param in zip(target.parameters(), source.parameters()):target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)def select_action(self, state, evaluate=False):"""选择动作 (训练与评估不同)"""state = torch.FloatTensor(state).unsqueeze(0)if evaluate:# 评估时使用均值 (图3a)mean, _ = self.policy(state)action = torch.tanh(mean)return action.detach().numpy()[0]else:# 训练时采样action, _ = self.policy.sample(state)return action.detach().numpy()[0]def train(self, env, episodes, batch_size=256):for episode in range(episodes):state = env.reset()episode_reward = 0while True:# 选择并执行动作action = self.select_action(state)next_state, reward, done, _ = env.step(action)# 存储经验self.replay_buffer.push(state, action, reward, next_state, done)episode_reward += reward# 状态转移state = next_state# 更新网络if len(self.replay_buffer) > batch_size:self.update(batch_size)if done:break