神经网络：深度剖析过拟合、欠拟合及其泛化能力提升策略

---

前言

欢迎继续关注深度学习，今天我们将继续在深度学习的海洋中遨游。过拟合，欠拟合，正则化，一个个概念将会渐渐的浮出水面。那么，读者们，你们准备好了吗，跟随笔者的脚步一起出发吧。

---

一、神经网络的过拟合

1.1 过拟合的概念

过拟合是指模型过于复杂，对训练数据的拟合能力过强，导致模型在训练数据上表现良好，但在测试数据上表现较差（泛化能力差）。

• 示意图解释 (训练/验证错误率与提前停止策略)
  

  • 横轴：训练迭代次数。
  • 纵轴：错误率。
  • 训练集（虚线）：错误率随迭代持续下降（模型持续学习）。
  • 验证集（实线）：前期错误率随训练同步下降，但迭代超过临界点后，错误率开始反弹（模型开始“死记硬背”训练集细节，对新数据（验证集）表现变差，即过拟合）。
  • 提前停止：在验证集错误率触底反弹前及时终止训练（如虚线标注处），可以避免模型过拟合，保留较好的泛化能力。
  • 总结：当验证集效果从变好转向变差时，应及时停止训练，防止模型过拟合。

• 造成过拟合的常见原因：

  • 数据量不足：模型容易过度学习训练数据中的噪声和细节。
  • 模型过于复杂：会过度学习训练数据的细节和噪声。
  • 正则化强度不足：模型易过度学习训练数据细节和噪声。
  • 数据量比例不均衡（“长尾效应”）：复杂模型容易将少量特例误判为噪声而去除，忽视真实存在的低频特征，引发识别偏差。

• 过拟合现象示例：模型学习的“细节”特征过多，导致识别新动物时，会因“细节”特征不匹配而识别结果不准确。
  

1.2 欠拟合与过拟合的区别

• 欠拟合：因模型学习能力不足，未能捕捉数据中的复杂关系。
• 过拟合：因模型学习能力过强，过度学习了训练数据的细节和噪声，导致泛化能力差。

1.3 代码示例

import numpy as np # 用于数值计算，特别是处理数据
import torch # PyTorch深度学习框架核心库
import torch.nn as nn # PyTorch神经网络模块，用于构建模型层
import matplotlib.pyplot as plt # 用于绘图，可视化训练过程和结果# 1. 准备数据集
# 定义一些数据点，这是一个简单的回归问题的数据集
# 第一列是特征（x），第二列是标签（y）
points = np.array([[-0.5, 7.7], [1.2, 65.8], [0.4, 39.2], [-1.4, -15.7],[1.5, 75.6], [0.4, 34.0], [0.8, 62.3]])# 将Numpy数组的特征列和标签列分离
x_train = points[:, 0] # 特征数据
y_train = points[:, 1] # 标签数据# 2. 定义神经网络模型
# PyTorch中所有的神经网络模块都应该继承自 nn.Module
class Model(nn.Module):# 构造函数：定义模型的层结构def __init__(self):super(Model, self).__init__() # 调用父类nn.Module的构造函数# 定义第一个全连接层（线性层）：# 输入特征1个 (x值)，输出特征2个。# 这一层将输入数据映射到2维空间，可以看作是学习输入的一些中间表示。self.layer1 = nn.Linear(1, 2)# 注释掉的层表示可以尝试更深的网络结构，例如：# self.layer2 = nn.Linear(16, 32)# self.layer3 = nn.Linear(32, 16)# 定义第二个全连接层（线性层）：# 输入特征2个 (来自layer1的输出)，输出特征1个 (最终的预测y值)。self.layer4 = nn.Linear(2, 1)# 前向传播函数：定义数据流经模型的路径def forward(self, x):# 经过第一个全连接层后，通常会跟着一个非线性激活函数# 这里使用 tanh (双曲正切) 激活函数，引入非线性能力，使得模型可以学习非线性关系。x = torch.tanh(self.layer1(x))# 如果有其他层，也会在这里定义它们的计算和激活函数# x = torch.relu(self.layer2(x))# x = torch.relu(self.layer3(x))# 最后一层是回归任务的输出层，通常不需要激活函数# 因为回归任务的目标是预测连续值，激活函数可能会限制输出范围（例如sigmoid会限制在0-1，tanh在-1-1）。x = self.layer4(x)return x# 实例化模型
model = Model()# 3. 定义损失函数和优化器
# 定义学习率（Learning Rate），控制模型参数更新的步长
lr = 0.05
# 定义损失函数：这里使用均方误差（MSELoss），适用于回归问题
# 它计算预测值和真实值之间差的平方的平均值，误差越小表示模型拟合得越好。
cri = torch.nn.MSELoss()
# 定义优化器：Adam优化器是一种常用的自适应学习率优化器
# 它会自动调整每个参数的学习率，通常在大多数任务中效果较好且易于使用。
# model.parameters() 会返回模型中所有可学习的参数（权重和偏置）
optimizer = torch.optim.Adam(model.parameters(), lr=lr)# 7. 绘图设置
# 创建一个包含两个子图的画布：一个用于展示数据拟合，一个用于展示损失曲线
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
# 用于存储每个epoch的编号，用于绘制损失曲线
epoch_list = []
# 用于存储每个epoch的损失值，用于绘制损失曲线
loss_list = []# 4. 开始训练迭代
epoches = 1000 # 训练的总轮数（epoch），表示整个数据集将被模型训练的次数
for epoch in range(1, epoches + 1):# 将Numpy数据转换为PyTorch张量（Tensor）# x_train_tensor: (num_samples,) -> (num_samples, 1)# unsqueeze(1) 用于在第二个维度（索引1）增加一个维度，以符合nn.Linear层的输入要求。# 例如，如果原始是 [x1, x2, x3]，nn.Linear需要 [[x1], [x2], [x3]] 这样的形状。x_train_tensor = torch.tensor(x_train, dtype=torch.float32).unsqueeze(1)# y_train_tensor: (num_samples,)y_train_tensor = torch.tensor(y_train, dtype=torch.float32)# 将数据输入模型进行前向传播，得到预测结果pre_result = model(x_train_tensor)# 计算损失：# pre_result的形状可能是 (num_samples, 1)，而y_train_tensor是 (num_samples,)。# squeeze(1) 用于去除pre_result中多余的维度（如果维度大小为1），使其形状与y_train_tensor一致，# 这样损失函数才能正确比较。loss = cri(pre_result.squeeze(1), y_train_tensor)# 记录损失值，.detach() 创建一个不参与梯度计算的新张量，.numpy() 将张量转换为Numpy数组，以便于绘图。loss_list.append(loss.detach().numpy())epoch_list.append(epoch) # 记录当前epoch# 优化器步骤：optimizer.zero_grad() # 梯度清零：在每次反向传播之前，将模型参数的梯度清零。# 这是因为PyTorch默认会累积梯度，如果不清零会导致错误更新。loss.backward()       # 反向传播：根据损失函数计算模型参数的梯度。optimizer.step()      # 参数更新：根据计算出的梯度和优化器（Adam）的规则更新模型的权重和偏置。# 5. 显示和绘图频率设置# 每隔20个epoch或在第一个epoch时打印损失并更新图像，以便观察训练过程。if epoch == 1 or epoch % 20 == 0:# 打印当前epoch和损失值，.item() 从单元素张量中获取Python数字，:.4f 格式化为4位小数。print(f"Epoch: {epoch}, Loss: {loss.item():.4f}")# 6. 实时绘图# 清除第一个子图的内容，准备绘制新的拟合曲线ax1.cla()ax1.set_title(f'Data Fit at Epoch {epoch}') # 设置子图标题ax1.set_xlabel('X') # 设置X轴标签ax1.set_ylabel('Y') # 设置Y轴标签ax1.scatter(x_train, y_train, label='True Data') # 绘制原始数据点# 生成用于绘制拟合曲线的X范围，从-2到2取100个点x_range = torch.tensor(np.linspace(-2, 2, 100), dtype=torch.float32)# 使用当前模型对整个X范围进行预测，得到拟合曲线的Y值y_range = model(x_range.unsqueeze(1))# 绘制拟合曲线，将张量转换为Numpy数组并去除多余维度。ax1.plot(x_range.detach().numpy(), y_range.detach().numpy().squeeze(1), color='red', label='Model Fit')ax1.legend() # 显示图例# 清除第二个子图的内容，准备绘制新的损失曲线ax2.cla()ax2.set_title('Loss Curve') # 设置子图标题ax2.set_xlabel('Epoch') # 设置X轴标签ax2.set_ylabel('Loss') # 设置Y轴标签ax2.plot(epoch_list, loss_list, color='blue') # 绘制损失曲线plt.pause(0.1) # 暂停0.1秒，以便观察图像的动态更新过程。如果设为1秒则更新较慢。# 训练结束后显示最终图像，保持窗口打开直到用户手动关闭
plt.show()

---

二、正则化 (Regularization)

正则化是一种通过在损失函数中添加正则化项来控制模型复杂度、防止过拟合的技术。

• 目的： 解决机器学习中复杂模型易过拟合（训练表现好、新数据泛化差）的问题。
• 原理： 通过约束模型参数来抑制模型复杂度。
• 常见类型： L1 正则化 和 L2 正则化。

2.1 损失函数的基础形式

在添加正则化项之前，原始损失函数（例如均方误差）通常表示为：

$loss(w,b)={\sum }_{i=1}^t(\widehat{y_i}-y{)}^2$

2.2 L1 正则化

当损失函数加入L1正则化项后，其形式变为：

$loss(w,b)={\sum }_{i=1}^t(\widehat{y_i}-y{)}^2+\lambda \cdot (|w_1|+|w_2|+|w_3|+...+|w_m|)$

• L1正则化项： $|w_1|+|w_2|+|w_3|+...+|w_m|$ (即模型权重绝对值之和)。
• $\lambda$： 正则化率，控制正则化项对总损失的影响程度。

2.3 L2 正则化

当损失函数加入L2正则化项后，其形式变为：

$loss(w,b)={\sum }_{i=1}^t(\widehat{y_i}-y{)}^2+\lambda \cdot ((w_1{)}^2+(w_2{)}^2+(w_3{)}^2+...+(w_m{)}^2)$

• L2正则化项： $(w_1{)}^2+(w_2{)}^2+(w_3{)}^2+...+(w_m{)}^2$ (即模型权重平方和)。
• $\lambda$： 正则化率，控制正则化项对总损失的影响程度。
  好的，这是一份经过整理和优化的内容，旨在更清晰、更结构化地解释正则化如何解决过拟合：

2.4 为什么正则化可以解决过拟合？

核心思想： 正则化通过在模型的损失函数中引入一个额外的惩罚项，来约束模型参数的大小，从而降低模型的复杂度，使其更倾向于学习数据的通用规律而非训练数据中的噪声，最终提升模型的泛化能力。

1. 正则化的作用机制

当加入正则化项后，模型的优化目标变为：

新的损失函数 = 原损失 (如 MSE/交叉熵) + 正则化项

以 L1/L2 正则化为例，这个正则化项（例如 $\lambda \sum |w_i|$ 或 $\lambda \sum w_i^2$）会对模型参数 $w$ 的大小进行惩罚。它迫使模型在最小化原损失的同时，也尽可能地使参数 $w$ 的值趋向于零或保持在较小的范围内。

2. 参数大小与解决过拟合的关系

• 过拟合的本质：
  模型在训练数据上表现极好，但由于其结构过于复杂或参数值过大，过度学习了训练数据中的噪声和特有模式，导致在未见过的新数据上表现不佳（泛化能力差）。大参数意味着模型对输入数据的微小变化（包括噪声）非常敏感，容易产生复杂的、波动大的决策边界或拟合曲线。

• 参数越小 = 模型越简单 (更鲁棒)：

  • 限制拟合能力： 当参数 $w$ 的绝对值趋近于零时，它们对模型输出的影响减小。这意味着模型对每个特征的依赖性降低，从而限制了模型捕捉训练数据中微小波动和噪声的能力。
  • 削弱噪声特征： 对于那些主要反映数据噪声的特征，正则化会倾向于将它们对应的参数惩罚至接近零，有效削弱这些噪声特征对模型决策的影响。
  • 降低模型复杂度： 较小的参数使模型变得更“平滑”或“线性化”（在多项式拟合中，高次项的系数趋近于零，使得曲线更趋于低次曲线；在神经网络中，更小的权重意味着激活函数的输入更接近其线性区域，使得网络整体更“不激进”），从而降低了模型的整体复杂度。

3. 总结

正则化通过“惩罚大参数”的机制，有效地“压缩”了模型的表达能力。它迫使模型放弃对训练数据中所有细节（包括噪声）的“记忆”，转而专注于学习数据背后更普遍、更本质的“通用规律”。这种从“记忆”到“学习”的转变，是提升模型泛化性能、解决过拟合问题的关键。

4. 示例：曲线拟合散点

假设我们有一些散点数据，并尝试用多项式进行拟合。

• 高次多项式拟合： 如果使用一个高次多项式（例如 $y=a+b\cdot x+c\cdot x^2+d\cdot x^3+e\cdot x^4$）来拟合，模型可能能够完美地穿过所有训练数据点，甚至包括那些由噪声引起的异常点。此时，高次项的参数（$c,d,e$）可能会变得非常大，导致拟合曲线高度弯曲，在训练点之间出现剧烈波动。这就是过拟合。

• 正则化后的效果：
  加入正则化后，高次项的参数（$c,d,e$）会受到惩罚，迫使它们趋近于 0。当这些参数趋近于 0 时，整个高次多项式实际上会“退化”成一个更简单的模型，例如接近直线（$a+b\cdot x$）或低次曲线。

  例如，如果 $c,d,e$ 都被正则化到接近 0，那么 $y\approx a+b\cdot x$，模型就从一个复杂的四次多项式简化成了一条直线。

  这种简化后的模型更平滑，对训练数据中的噪声不敏感，因此对未知数据点的泛化能力更强，能够实现更优的、更鲁棒的拟合效果。

2.5 正则化的核心思想

正则化的主要目标是避免模型过拟合。其实现方式是在模型的损失函数中引入一个额外的项。这个额外项通常与模型的复杂度（例如，模型参数的L1或L2范数）相关。通过一个正则化参数λ来控制此项的权重，模型会因复杂度受到惩罚，从而促使模型学习到更简单、泛化能力更好的参数。

2.6 为什么只对权重参数W添加惩罚？

在正则化中，通常只对模型的权重参数W施加惩罚，而偏置项b不被正则化。原因如下：

• 偏置项b的作用： 偏置项b仅控制拟合曲线或决策边界在y轴上的整体平移，它不改变曲线的形状或模型的倾斜度。
• 正则化的目标： 正则化的根本目的是通过惩罚模型的复杂度来使曲线平滑，减少模型对训练数据的敏感度，从而避免过拟合。这主要是通过限制权重参数W的取值范围或使其稀疏化来实现的。
• 对b正则化的意义： 由于b只影响模型的整体位置而不影响其复杂性或形状，对其施加正则化惩罚没有实际意义，也无法达到防止过拟合的效果。

好的，我来为您整理和归纳这段关于 L1 和 L2 正则化的内容。

---

2.7 L1 正则化与 L2 正则化对比

我们以一个包含两个参数 $w_1,w_2$ 的模型为例，通过几何直观来理解 L1 和 L2 正则化的原理及差异。

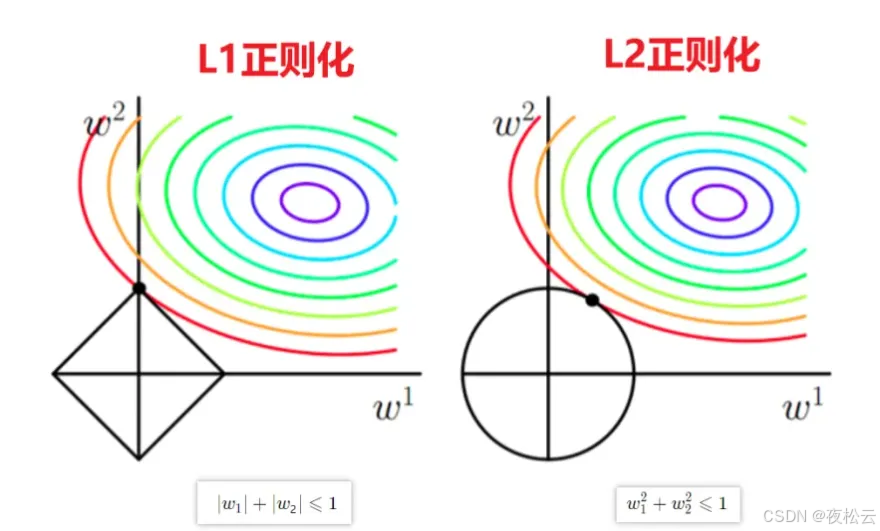
L1 正则化 (Lasso 回归)

• 几何约束： L1 正则化的约束区域是一个菱形（或称作 $L_1$ 范数球），其数学表达式为：

  $|w_1|+|w_2|\le 1$

  这对应于图中的左图。

• 对参数的影响：

  • 稀疏性： 由于菱形约束区域在坐标轴上存在尖角，当损失函数的等高线（图中彩色圈，其中心为无约束条件下的最小损失）与菱形区域相切时，切点（即最优解）更容易落在坐标轴上（例如 $w_1=0$ 或 $w_2=0$）。
  • 特征选择： 这意味着 L1 正则化倾向于将某些不重要特征的参数（权重）精确地压缩为零，从而实现特征选择，产生一个稀疏的模型。这有助于简化模型，提高模型的可解释性。

L2 正则化 (Ridge 回归)

• 几何约束： L2 正则化的约束区域是一个圆形（或称作 $L_2$ 范数球），其数学表达式为：

  $w_1^2+w_2^2\le 1$

  这对应于图中的右图。

• 对参数的影响：

  • 参数平滑缩小： 圆形的边界是平滑的。当损失函数的等高线（彩色圈）与圆形约束区域相切时，切点通常不会精确地落在坐标轴上。
  • 抑制过拟合： L2 正则化会促使所有参数的值向零均匀缩小，但很少会将参数完全变为零。它主要用于减少参数的震荡，防止模型权重过大，从而有效地抑制过拟合，提高模型的稳定性。

• 损失函数形式： 在实际应用中，L2 正则化通常是将惩罚项直接加到原损失函数中，形成总损失函数：

  $Los{s}_{总}=Los{s}_{原损失}+\frac{1}{2}\lambda \sum w^2$

  其中，$\lambda$ 是正则化强度参数，用于控制正则化的强度；系数 $1/2$ 的加入主要是为了在反向传播求导时，使得求导结果更简洁（平方项的导数为 $2w$，与 $1/2$ 抵消）。

特性	L1 正则化 (Lasso)	L2 正则化 (Ridge)
约束区域	菱形 ($	w_1
惩罚方式	对参数绝对值之和进行惩罚 ($L_1$ 范数)	对参数平方和进行惩罚 ($L_2$ 范数)
对参数影响	稀疏化，部分参数变为 0	平滑缩小，参数趋近于 0 但不完全为 0
主要用途	特征选择、简化模型、提高可解释性	防止过拟合、减少参数震荡、提高模型稳定性
几何原理	损失等高线易与菱形尖角相切	损失等高线与圆形平滑曲线相切

总结：L1 和 L2 正则化都是通过限制模型参数的“大小”来惩罚模型的复杂度。L1 倾向于产生稀疏解，可用于特征选择；L2 倾向于使参数平滑缩小，更注重模型的稳定性和泛化能力。在实际应用中，选择哪种正则化方法取决于具体的需求：如果需要进行特征选择或模型解释性较强，L1 是一个好选择；如果主要目标是防止过拟合并使模型更稳定，L2 则更常用。

2.8 代码示例

import numpy as np  # 导入NumPy库，用于进行数值计算和数组操作
import torch  # 导入PyTorch库，用于构建和训练神经网络
import torch.nn as nn  # 导入PyTorch的神经网络模块，包含了各种层、激活函数、损失函数等
import matplotlib.pyplot as plt  # 导入Matplotlib库，用于数据可视化和绘图# 确保初始化的值都一样，以保证实验的可复现性
seed = 42  # 设置随机种子，一个固定的整数值
torch.manual_seed(seed)  # 为CPU设置随机种子，确保每次运行程序时，涉及到随机操作（如模型参数初始化）的结果都是一致的# 1. 创造数据，数据集
# 定义一组二维点数据，每个点包含一个特征（x）和一个标签（y）
points = np.array([[-0.5, 7.7], [1.2, 65.8], [0.4, 39.2], [-1.4, -15.7],[1.5, 75.6], [0.4, 34.0], [0.8, 62.3]])
# 从数据集中分离特征和标签
x_train = points[:, 0]  # 特征数据，取所有行的第0列（x值）
y_train = points[:, 1]  # 标签数据，取所有行的第1列（y值）# 2. 定义前向模型（神经网络结构）
class Model(nn.Module):  # 定义一个名为Model的类，它继承自torch.nn.Module，这是所有神经网络模块的基类# 定义初始化函数，用于构建模型的层def __init__(self):super(Model, self).__init__()  # 调用父类nn.Module的构造函数，这是PyTorch模型定义的标准做法# 定义一系列全连接层（线性层）# nn.Linear(in_features, out_features) 创建一个全连接层# layer1: 输入特征维度1（x值），输出特征维度16self.layer1 = nn.Linear(1, 16)# layer2: 输入特征维度16，输出特征维度32self.layer2 = nn.Linear(16, 32)# layer3: 输入特征维度32，输出特征维度16self.layer3 = nn.Linear(32, 16)# layer4: 输入特征维度16，输出特征维度1（因为是回归问题，最终输出一个预测值）self.layer4 = nn.Linear(16, 1)# 定义前向传播过程（数据如何流经网络）def forward(self, x):# 线性层后都跟着激活函数（这里使用ReLU），以引入非线性性，使模型能够学习更复杂的模式x = torch.relu(self.layer1(x))  # 数据通过layer1后，应用ReLU激活函数x = torch.relu(self.layer2(x))  # 数据通过layer2后，应用ReLU激活函数x = torch.relu(self.layer3(x))  # 数据通过layer3后，应用ReLU激活函数# 最后一层是用于拟合回归结果，通常不使用激活函数，直接输出原始预测值x = self.layer4(x)  # 数据通过layer4，得到最终的预测输出return x  # 返回模型的预测结果model = Model()  # 实例化（创建）一个Model类的对象，即我们的神经网络模型# 3. 定义损失函数和优化器
# 定义学习率（lr），控制模型参数更新的步长
lr = 0.05
# 定义损失函数，这里是回归问题，使用均方误差（MSELoss）作为损失函数
# MSELoss计算预测值与真实值之间差值的平方的平均值，衡量模型预测的准确性
cri = torch.nn.MSELoss()
# 定义优化器，这里使用Adam优化器
# Adam是一种自适应学习率优化算法，通常效果较好且鲁棒性强
# model.parameters() 告诉优化器需要更新哪些参数（模型的权重和偏置）
# lr=lr 设置学习率
# weight_decay=0.2 添加L2正则化（权重衰减）。它通过向损失函数添加模型权重的平方和（乘以一个系数0.2）来惩罚大的权重值，
# 有助于防止模型过拟合，提高泛化能力
optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=1)# 7. 画图（初始化绘图界面）
# 创建一个包含1行2列子图的图形，并设置图形大小
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
epoch_list = []  # 用于存储每个epoch的编号，用于绘制损失曲线
loss_list = []  # 用于存储每个epoch的损失值，用于绘制损失曲线# 4. 开始迭代训练模型
epoches = 1000  # 设置训练的总迭代次数（epoch数量）
for epoch in range(1, epoches + 1):  # 循环迭代每个epoch# 数据转化为PyTorch张量（tensor），并指定数据类型为float32# .unsqueeze(1) 将x_train从形状 (N,) 变为 (N, 1)，# 因为nn.Linear层期望输入是 (batch_size, in_features) 的形状，这里的in_features是1x_train_tensor = torch.tensor(x_train, dtype=torch.float32).unsqueeze(1)# y_train_tensor无需unsqueeze，因为MSELoss通常可以处理 (N,) 或 (N, 1) 形状的标签y_train_tensor = torch.tensor(y_train, dtype=torch.float32)# 数据输入模型进行前向传播，得到预测结果pre_result = model(x_train_tensor)# 计算损失# pre_result.squeeze(1) 将模型的输出从 (N, 1) 形状变为 (N,)，# 以便与y_train_tensor的形状匹配，方便损失函数计算loss = cri(pre_result.squeeze(1), y_train_tensor)loss_list.append(loss.detach().numpy())  # 记录当前epoch的损失值，.detach().numpy() 将张量转换为NumPy数组，并断开计算图epoch_list.append(epoch)  # 记录当前epoch的编号# 优化更新模型参数optimizer.zero_grad()  # 在反向传播之前，清零模型的所有梯度。这是PyTorch的惯例，防止梯度累积loss.backward()  # 执行反向传播，计算损失对模型参数的梯度optimizer.step()  # 根据计算出的梯度和优化器设定的学习率，更新模型的参数（权重和偏置）# 5. 显示频率设置：每隔20个epoch或在第一个epoch时显示训练信息和绘图if epoch == 1 or epoch % 20 == 0:print(f"epoch:{epoch},loss:{loss:.4f}")  # 打印当前epoch数和损失值，保留4位小数# 6. 绘图：实时更新模型拟合情况和损失曲线ax1.cla()  # 清除第一个子图（模型拟合图）的内容ax1.scatter(x_train, y_train, label='Original Data')  # 在第一个子图上绘制原始数据点ax1.set_title('Model Fitting')ax1.set_xlabel('X')ax1.set_ylabel('Y')# 创建一个更密集的x值范围，用于绘制模型当前的拟合曲线x_range = torch.tensor(np.linspace(-2, 2, 100), dtype=torch.float32)# 使用模型对x_range进行预测，得到对应的y值y_range = model(x_range.unsqueeze(1))# 在第一个子图上绘制模型当前的拟合曲线# .detach().numpy().squeeze(1) 将预测结果从张量转换为NumPy数组，并移除单维维度ax1.plot(x_range.detach().numpy(), y_range.detach().numpy().squeeze(1), color='red', label='Model Prediction')ax1.legend()ax1.grid(True)ax2.cla()  # 清除第二个子图（损失曲线图）的内容ax2.plot(epoch_list, loss_list, color='blue')  # 在第二个子图上绘制损失值随epoch变化的曲线ax2.set_title('Loss Curve')ax2.set_xlabel('Epoch')ax2.set_ylabel('Loss')ax2.grid(True)plt.tight_layout()  # 自动调整子图参数，使之填充整个图像区域plt.pause(0.1)  # 暂停一小段时间（0.01秒），以便Matplotlib更新图像并显示动画效果plt.show()  # 训练结束后，保持窗口显示最终的图形，直到手动关闭

---

三、神经网络的欠拟合与过拟合及其解决方案

3.1 欠拟合及其解决方案

• 原因： 数据量不足、模型过于简单。
• 解决方案：
  • 增加样本数据集。
  • 增加神经网络隐藏层的层数，使模型更复杂。

3.2 过拟合及其解决方案

• 原因： 模型过于复杂或数据量太少，导致过度学习训练模型中的细节和噪声。

• 常见解决方案：

  3.2.1 正则化 (Regularization)

  • 核心思想： 通过向损失函数添加正则化项来惩罚模型参数的大小。
  • 类型： L1 正则化和 L2 正则化。
  • 目的： 抑制模型复杂度，从而抑制过拟合。

  3.2.2 Dropout (随机失活)

  • 核心思想： 在神经网络训练过程中，随机地“丢弃”（即将其输出置为0）部分神经元。
  • 工作原理：
    • 降低模型对特定神经元的依赖： 迫使网络学习对神经元变化更鲁棒的特征，防止过度依赖某些特征。
    • 减少复杂度： 暂时性地减少了网络中神经元之间的复杂连接，降低了模型的有效复杂度。
    • 增强泛化能力： 促使网络学习更泛化的特征，减少对训练数据的过拟合。
  • 应用示例： 若某层有4个神经元，应用Dropout（参数0.5）意味着每个节点有50%的概率被随机置为0，例如原始输出[0.7, 0.2, 0.9, 0.5]可能变为[0.7, 0, 0.9, 0]。被置0的节点暂不参与前后层的连接计算。
    
    

  3.2.3 Inverted Dropout (反向丢弃法)

  • 目的： 简化测试阶段的操作。
  • 训练时： 按Dropout概率随机舍弃神经元后，对保留的神经元输出进行按比例缩放（通常是除以保留率keep_prob = 1 - drop_prob）。
    • 示例代码：Y = mask * X / keep_prob
  • 测试时： 保留所有神经元，无需额外缩放。

  3.2.4 Dropout解决过拟合的原因

  • 1. 抑制对特定神经元的依赖：
    • 标准神经网络容易过度依赖某些特定神经元。
    • Dropout通过随机丢弃神经元，迫使网络学习更具鲁棒性的特征，降低对训练数据的过拟合。
  • 2. 等效于模型平均：
    • 在训练时，随机丢弃神经元相当于训练了多个结构不同的“子网络”。
    • 在测试时，使用完整的网络进行预测，其结果等效于对这些不同子网络输出的平均，通过这种“综合抵消”的方式减轻了过拟合。

3.3 代码示例

import numpy as np  # 导入NumPy库，用于数值计算，特别是处理数组
import torch  # 导入PyTorch库，一个开源机器学习框架
import torch.nn as nn  # 导入PyTorch的神经网络模块，用于构建神经网络层
import torch.optim as optim  # 导入PyTorch的优化器模块，用于更新模型参数
import matplotlib.pyplot as plt  # 导入Matplotlib的pyplot模块，用于数据可视化和绘图# 1. 散点输入 (Scatter Input Data)
# 定义第一类点的坐标数据
class1_points = np.array([[-0.7, 0.7], [3.9, 1.5], [1.7, 2.2], [1.9, -2.4], [0.9, 1.4], [4.2, 0.9], [1.7, 0.7], [0.2, -0.2],[3.1, -0.4],[-0.2, -0.9], [1.7, 0.2], [-0.6, -3.9], [-1.8, -4.0], [0.7, 3.8], [-0.7, -3.3], [0.8, 1.8], [-0.5, 1.5],[-0.6, -3.6], [-3.1, -3.0], [2.1, -2.5], [-2.5, -3.4], [-2.6, -0.8], [-0.2, 0.9], [-3.0, 3.3],[-0.7, 0.2],[0.3, 3.0], [0.6, 1.9], [-4.0, 2.4], [1.9, -2.2], [1.0, 0.3], [-0.9, -0.7], [-3.7, 0.6], [-2.7, -1.5],[0.9, -0.3],[0.8, -0.2], [-0.4, -4.4], [-0.3, 0.8], [4.1, 1.0], [-2.5, -3.5], [-0.8, 0.3], [0.6, 0.6], [2.6, -1.0],[1.8, 0.4],[1.5, -1.0], [3.2, 1.1], [3.3, -2.5], [-3.8, 2.5], [3.1, -0.9], [3.4, -1.1], [0.3, 0.8], [-0.1, 2.9],[-2.8, 1.9],[2.8, -3.3], [-1.0, 3.1], [-0.8, -0.6], [-2.5, -1.5], [0.3, 0.2], [-1.0, -2.9], [0.7, 0.2], [-0.5, 0.9],[-0.8, 0.7], [4.1, 0.5], [2.8, 2.3], [-3.9, 0.1], [2.2, -1.4], [-0.7, -3.5], [1.0, 1.2], [-0.7, -4.0],[1.3, 0.6],[-0.1, 3.3], [0.0, -0.3], [1.8, -3.0], [0.6, 0.0], [3.6, -2.8], [-3.9, -0.9], [-4.3, -0.9], [0.1, -0.8],[-1.6, -2.7], [-1.8, -3.3], [1.7, -3.5], [3.6, -3.1], [-2.4, 2.5], [-1.0, 1.8], [3.9, 2.5],[-3.9, -1.3],[3.4, 1.6], [-0.1, -0.6], [-3.7, -1.3], [-0.3, 3.4], [-3.7, -1.7], [4.0, 1.1], [3.4, 0.2], [0.1, -1.6],[-1.2, -0.5], [2.4, 1.7], [-4.4, -0.5], [-0.2, -3.6], [-0.8, 0.4], [-1.5, -2.2], [3.9, 2.5], [4.4, 1.4],[-3.5, -1.1], [-0.7, 1.5], [-3.0, -2.6], [0.2, -3.5], [0.0, 1.2], [-4.3, 0.1], [-1.8, 2.8], [1.1, -2.5],[0.2, 4.3], [-3.9, 2.2], [1.0, 1.6], [4.5, 0.2], [3.9, -1.6], [-0.4, -0.5], [0.3, -0.4], [-3.2, 1.7],[2.0, 4.1],[2.5, 2.2], [-1.1, -0.3], [-3.7, -1.9], [1.5, -1.1], [-2.1, -1.9], [-0.1, 4.5], [3.8, -0.3],[-0.9, -3.8],[-2.9, -1.6], [1.0, -1.2], [0.7, 0.0], [-0.8, 3.3], [-2.8, 3.1], [0.4, -3.2], [4.6, 1.0], [2.5, 3.1],[4.2, 0.8],[3.6, 1.8], [1.4, -3.0], [-0.4, -1.4], [-4.1, 1.1], [1.1, -0.2], [-2.9, -0.0], [-3.5, 1.3], [-1.4, 0.0],[-3.7, 2.2], [-2.9, 2.8], [1.7, 0.4], [-0.8, -0.6], [2.9, 1.1], [-2.3, 3.1], [-2.9, -2.0], [-2.7, -0.4],[2.6, -2.4], [-1.7, -2.8], [1.2, 3.1], [3.8, 1.3], [0.1, 1.9], [-0.5, -1.0], [0.0, -0.5], [3.9, -0.7],[-3.7, -2.5], [-3.1, 2.7], [-0.9, -1.0], [-0.7, -0.8], [-0.4, -0.1], [1.5, 1.0], [-2.6, 1.9],[-0.8, 1.7],[0.8, 1.8], [2.0, 3.6], [3.2, 1.4], [2.3, 1.4], [4.9, 0.5], [2.2, 1.8], [-1.4, -2.7], [3.1, 1.1],[-1.0, 3.8],[-0.4, -1.1], [3.3, 1.1], [2.2, -3.9], [1.0, 1.2], [2.6, 3.2], [-0.6, -3.0], [-1.9, -2.8], [1.2, -1.2],[-0.4, -2.7], [1.1, -4.3], [0.3, -0.8], [-1.0, -0.4], [-1.1, -0.2], [0.1, 1.2], [0.9, 0.6], [-2.7, 1.6],[1.0, -0.7], [0.3, -4.2], [-2.1, 3.2], [3.4, -1.2], [2.5, -4.0], [1.0, -0.8], [1.0, -0.9], [0.1, -0.6]])
# 定义第二类点的坐标数据
class2_points = np.array([[-3.0, -3.8], [4.4, 2.5], [2.6, 4.1], [3.7, -2.7], [-3.7, -2.9], [5.3, 0.3], [3.9, 2.9], [-2.7, -4.5],[5.4, 0.2],[3.0, 4.8], [-4.2, -1.3], [-2.1, -5.4], [-3.2, -4.6], [0.7, 4.5], [-1.4, -5.7], [0.5, 5.9], [-2.1, 4.0],[-0.1, -5.1], [-3.4, -4.7], [3.3, -4.7], [-2.7, -4.1], [-4.5, -2.0], [4.3, 2.9], [-3.6, 4.0],[-0.5, 5.5],[0.2, 5.2], [5.3, -0.9], [-4.5, 3.6], [3.4, -2.8], [-3.4, -3.7], [1.6, -5.5], [-5.9, -0.1],[-4.8, -2.5],[-5.5, 0.3], [1.6, 4.4], [-0.9, -5.3], [-1.0, 5.4], [4.9, 0.8], [-3.1, -4.0], [2.3, 4.7], [4.0, -1.6],[4.9, -1.5],[4.2, -2.5], [-3.5, 3.7], [4.7, 0.5], [5.3, -2.6], [-5.0, 2.4], [5.5, -1.2], [5.6, -1.3], [3.3, -4.3],[-1.3, 4.4],[-4.1, 3.6], [3.3, -4.5], [-2.3, 5.2], [2.6, 4.6], [-4.4, -1.6], [4.7, -2.0], [-1.7, -4.9],[-5.1, -2.4],[4.5, 3.2], [-3.9, -3.4], [6.0, -0.4], [3.5, 4.3], [-4.9, -0.6], [3.3, -3.2], [-0.3, -4.8],[-1.6, -4.7],[-1.4, -4.6], [-3.1, 3.8], [-1.4, 4.9], [1.8, -4.5], [2.2, -5.5], [3.1, -3.4], [4.7, -2.8],[-5.3, -0.4],[-6.0, -0.1], [1.4, -4.5], [-3.1, -4.3], [-1.8, -5.7], [1.7, -5.6], [4.5, -3.7], [-2.6, 4.3],[-3.4, 3.4],[4.7, 3.1], [-5.2, -2.8], [5.4, 1.2], [-5.4, 1.2], [-4.9, -1.3], [-1.3, 5.6], [-4.1, -2.6], [5.0, 1.0],[5.2, 1.2],[2.4, -4.9], [-3.2, 3.8], [3.3, 3.4], [-5.5, -0.8], [0.6, -5.0], [1.2, 5.4], [-3.4, -3.3], [4.6, 2.8],[5.2, 1.7],[-4.4, -0.9], [-5.0, -1.3], [-3.1, -3.6], [-0.7, -4.5], [5.9, -0.9], [-5.1, -0.5], [-2.6, 5.2],[1.4, -4.8],[-0.7, 5.6], [-5.3, 2.1], [4.9, 2.6], [5.3, 0.9], [5.1, -1.2], [2.7, -4.4], [-2.0, -5.6], [-4.9, 3.2],[2.8, 5.3],[2.6, 3.9], [-0.0, 5.7], [-5.7, -1.8], [-1.1, -4.7], [-2.4, -3.8], [-1.1, 5.6], [5.3, -1.5],[-0.4, -5.8],[-4.5, -1.6], [-4.4, -3.7], [-4.3, 2.4], [0.1, 4.8], [-3.0, 3.8], [0.3, -5.8], [5.6, 0.5], [4.1, 3.6],[5.0, 1.5],[5.7, 1.5], [3.2, -4.1], [-1.7, -5.6], [-5.3, 0.9], [4.3, 3.0], [-5.4, 0.3], [-5.0, 0.8], [2.7, 5.1],[-5.0, 2.2],[-4.0, 3.0], [-4.4, -3.9], [-3.5, -3.9], [5.3, 1.5], [-4.2, 4.2], [-3.9, -4.0], [-4.7, -0.1],[3.7, -4.7],[-3.0, -4.7], [2.7, 4.4], [4.3, 2.0], [-3.6, -4.5], [5.5, 0.9], [-4.7, -2.8], [5.5, -2.2], [-5.1, -2.6],[-3.6, 3.1], [-3.2, -4.0], [-4.8, 1.3], [-5.5, -1.6], [4.1, -1.6], [-4.2, 3.6], [5.6, -1.4],[4.9, -3.3],[1.7, 4.9], [5.3, 2.5], [3.8, 2.8], [5.8, 0.7], [3.9, 2.6], [-2.1, -4.8], [5.2, 2.5], [-2.0, 4.3],[2.8, -4.1],[5.6, 0.8], [2.2, -5.2], [-1.1, 5.5], [4.2, 3.8], [-1.8, -5.2], [-3.4, -3.6], [3.7, -3.6], [-0.5, -4.8],[1.9, -5.6], [-1.1, 5.4], [2.3, 4.7], [0.0, -5.4], [2.1, -5.6], [4.8, -0.3], [-4.7, 2.9], [-3.8, 3.9],[0.9, -5.5],[-2.3, 3.6], [5.3, -2.5], [3.7, -4.6], [-5.0, 2.4], [0.0, -5.7], [0.2, -5.9]])# 合并两类点数据，形成完整的输入数据集
points = np.concatenate((class1_points, class2_points), axis=0)  # axis=0表示按行合并
print("Total points shape:", points.shape)  # 打印合并后数据的形状# 为两类点生成标签：0 表示类别1， 1 表示类别2
labels1 = np.zeros(len(class1_points))  # 为第一类点生成全0标签
labels2 = np.ones(len(class2_points))  # 为第二类点生成全1标签
labels = np.concatenate((labels1, labels2))  # 合并标签# 定义L2正则化的系数（惩罚项权重），用于控制正则化强度
regularizers1 = 0.01
regularizers2 = 0.01
regularizers3 = 0.01# 定义一个L2正则化项的函数
# model: 神经网络模型实例
# loss: 当前的损失值
# par: 用于指定对哪个层的参数进行正则化（通过名称匹配）
# reg_coff: 正则化系数
def L2_Reg(model, loss, par, reg_coff):L2_reg = 0  # 初始化L2正则化项为0# 计算L2正则化项# named_parameters()是 nn.Module中一个重要属性，它返回一个迭代器，包含模型中所有命名参数# 每个元素是一个 (name, parameter) 对，其中name是参数的名称，parameter是参数张量for name, param in model.named_parameters():# 检查参数名称是否包含指定的层名称 (par)# 并且只对“weight”（权重）参数进行正则化，通常不对“bias”（偏置）进行if par in name:if 'weight' in name:# pytorch求范数函数——torch.norm# 计算参数的L2范数 (欧几里得范数)L2_reg += torch.norm(param,  # 输入参数张量p=2  # 使用L2范数 (p=2))# 将计算出的L2正则化项（乘以其系数）添加到原始损失函数中loss += reg_coff * L2_regreturn loss# 2. 定义前向模型 (Define the Feedforward Model)
# ModelClass继承自nn.Module，这是所有神经网络模块的基类
class ModelClass(nn.Module):def __init__(self):# 调用父类nn.Module的构造函数super(ModelClass, self).__init__()# 定义全连接层 (Linear layers)# nn.Linear(in_features, out_features)# layer1: 输入特征2 (x, y坐标)，输出特征8self.layer1 = nn.Linear(2, 8)# layer2: 输入特征8，输出特征32self.layer2 = nn.Linear(8, 32)# layer3: 输入特征32，输出特征32self.layer3 = nn.Linear(32, 32)# layer4: 输入特征32，输出特征2 (对应两个类别)self.layer4 = nn.Linear(32, 2)# 定义Dropout层，用于防止过拟合# nn.Dropout(p=probability) 表示随机将输入单元的p%设置为0self.dropout1 = nn.Dropout(p=0.1)self.dropout2 = nn.Dropout(p=0.1)self.dropout3 = nn.Dropout(p=0.1)# 定义前向传播函数，数据x通过模型层进行计算def forward(self, x):# x通过layer1，然后应用ReLU激活函数x = torch.relu(self.layer1(x))# 应用dropout1x = self.dropout1(x)# x通过layer2，然后应用ReLU激活函数x = torch.relu(self.layer2(x))# 应用dropout2x = self.dropout2(x)# x通过layer3，然后应用ReLU激活函数x = torch.relu(self.layer3(x))# 应用dropout3x = self.dropout3(x)# x通过layer4# 二分类这里使用softmax加交叉熵，softmax将输出转换为概率分布# dim=1 表示对每个样本的特征维度（即类别分数）进行softmax操作x = torch.softmax(self.layer4(x), dim=1)return x# 实例化模型
model = ModelClass()# 3. 定义损失函数和优化器 (Define Loss Function and Optimizer)
lr = 0.001  # 定义学习率# 定义交叉熵损失函数 (Cross-Entropy Loss)
# 适用于多分类问题，在内部会进行softmax和负对数似然计算
cri = nn.CrossEntropyLoss()
# 定义优化器：Adam优化器
# model.parameters() 告诉优化器要优化的模型参数
# lr (learning rate) 设定学习步长
optimizer = optim.Adam(model.parameters(), lr=lr)# 7. 画图使用数据 (Data for Plotting)
# 根据输入点的范围，定义绘图区域的x和y轴的最小值和最大值
x_min, x_max = points[:, 0].min() - 1, points[:, 0].max() + 1
y_min, y_max = points[:, 1].min() - 1, points[:, 1].max() + 1
step_size = 0.1  # 定义网格点的步长，用于生成更平滑的决策边界# 创建网格点 (meshgrid)
# xx, yy 分别是x和y坐标的二维网格
xx, yy = np.meshgrid(np.arange(x_min, x_max, step_size),  # x轴范围内的点np.arange(y_min, y_max, step_size)  # y轴范围内的点)
# 将网格点展平并组合成 (x, y) 对，用于模型预测
grid_points = np.c_[xx.ravel(), yy.ravel()]
print("Grid points shape:", grid_points.shape)  # 打印网格点数据的形状# 7. 创建三维图形和右侧的二维子图 (Create 3D and 2D Subplots)
fig = plt.figure(figsize=(12, 8))  # 创建一个图形对象，并设置大小
# 添加第一个子图，设置为3D投影
ax1_3d = fig.add_subplot(121, projection='3d')  # 1行2列的第一个子图
# 添加第二个子图，设置为2D (默认)
ax2_2d = fig.add_subplot(122)  # 1行2列的第二个子图# 4. 开始迭代训练 (Start Training Iteration)
epoches = 500  # 定义训练的总轮数 (epoch)
batch_size = 8  # 定义每个批次处理的样本数量# 遍历每个训练周期 (epoch)
for epoch in range(1, epoches + 1):# 将模型设置为训练模式# 这会启用Dropout层和BatchNorm层 (如果使用的话)model.train()# 按照batch_size进行迭代，处理每个批次的数据for batch_start in range(0, len(points), batch_size):# 从数据集中获取当前批次的输入数据# torch.tensor() 将NumPy数组转换为PyTorch张量# dtype=torch.float32 是浮点型数据，适用于输入特征batch_inputs = torch.tensor(points[batch_start:batch_start + batch_size, :], dtype=torch.float32)# 从标签集中获取当前批次的标签数据# dtype=torch.long 是长整型数据，适用于分类任务的类别标签 (CrossEntropyLoss要求)batch_labels = torch.tensor(labels[batch_start:batch_start + batch_size], dtype=torch.long)# 前向传播 (Forward pass)outputs = model(batch_inputs)# 计算损失 (Calculate loss)loss = cri(outputs, batch_labels)# 添加正则化项 (Add regularization terms)# 分别对layer1、layer2、layer3的权重应用L2正则化loss = L2_Reg(model, loss, 'layer1', regularizers1)loss = L2_Reg(model, loss, 'layer2', regularizers2)loss = L2_Reg(model, loss, 'layer3', regularizers3)# 反向传播和优化 (Backward pass and optimization)# 清除之前计算的梯度，避免梯度累积optimizer.zero_grad()# 计算损失函数相对于模型参数的梯度loss.backward()# 根据梯度更新模型参数optimizer.step()# 将模型设置为评估模式# 这会禁用Dropout层，以便在评估时不随机丢弃神经元model.eval()# 5. 显示频率设置 (Display Frequency Setting)fre_display = 20  # 每隔20个epoch更新一次图# 显示与输出 (Display and Output)if epoch % fre_display == 0 or epoch == 1:# 使用训练好的模型预测网格点的标签# 将NumPy网格点数据转换为PyTorch张量grid_points_tensor = torch.tensor(grid_points, dtype=torch.float32)# 模型预测 (前向传播)pre_result = model(grid_points_tensor)# 取出第一类的概率值 (这里假设类别0是第一类，类别1是第二类)# pre_result[:, 0] 获取所有网格点对类别0的预测概率# .reshape(xx.shape) 将一维概率数组重新塑形为与xx相同的二维网格形状# .detach() 将张量从计算图中分离，防止后续操作影响梯度计算# .numpy() 将PyTorch张量转换为NumPy数组，以便Matplotlib绘图pre_prob_one_class = pre_result[:, 0].reshape(xx.shape).detach().numpy()# 清空ax1_3d子图，以便绘制新的内容（用于动画效果）ax1_3d.cla()# 在3D子图上绘制原始数据点# class1_points[:, 0] 是x坐标，class1_points[:, 1] 是y坐标# np.ones_like() 创建一个与输入数组形状相同、元素全为1的数组，用于3D散点的z坐标# 这里将类别1的点绘制在z=1的平面上ax1_3d.scatter(class1_points[:, 0], class1_points[:, 1], np.ones_like(class1_points[:, 0]), c='blue',label='class 1')# 将类别2的点绘制在z=0的平面上ax1_3d.scatter(class2_points[:, 0], class2_points[:, 1], np.zeros_like(class2_points[:, 0]), c='red',label='class 2')ax1_3d.legend()  # 显示图例# 绘制三维表面图 (decision surface)# xx, yy 是网格点的x, y坐标# pre_prob_one_class 是模型预测的类别0的概率，作为z坐标# alpha=0.5 设置表面透明度ax1_3d.plot_surface(xx, yy, pre_prob_one_class, alpha=0.5)# 在3D表面上绘制等高线，levels=[0.5] 表示绘制概率为0.5的等高线，即决策边界ax1_3d.contour(xx, yy, pre_prob_one_class, levels=[0.5], cmap='jet')# 设置3D图的轴标签和标题ax1_3d.set_xlabel('feature 1')ax1_3d.set_ylabel('feature 2')ax1_3d.set_zlabel('label')  # Z轴表示类别0的概率ax1_3d.set_title('hyperplane')  # 标题表示决策超平面# 清空ax2_2d子图，以便绘制新的内容ax2_2d.cla()# 在2D子图上绘制原始数据点ax2_2d.scatter(class1_points[:, 0], class1_points[:, 1], c='blue', label='Class 1')ax2_2d.scatter(class2_points[:, 0], class2_points[:, 1], c='red', label='Class 2')# 在2D子图上绘制决策边界等高线# levels=[0.5] 表示绘制概率为0.5的等高线，即分类边界ax2_2d.contour(xx, yy, pre_prob_one_class, levels=[0.5], colors='black')ax2_2d.set_xlabel('feature 1')  # 设置X轴标签ax2_2d.set_ylabel('feature 2')  # 设置Y轴标签ax2_2d.set_title('Decision Boundary')  # 设置标题ax2_2d.legend()  # 显示图例plt.tight_layout()  # 调整子图布局，防止重叠plt.pause(1)  # 暂停1秒，以便观察每次更新后的图plt.show()  # 显示最终的图表，程序保持运行直到窗口关闭

---

总结

本文深入探讨了神经网络模型训练中常见的过拟合与欠拟合问题及其解决方案。过拟合表现为模型在训练数据上表现良好但在未见过的新数据上泛化能力差，通常由数据量不足、模型复杂度过高或正则化强度不足引起；欠拟合则因模型学习能力不足导致其无法捕捉数据中的复杂关系。为解决这些问题，文章详细介绍了正则化技术（L1和L2），它们通过在损失函数中增加惩罚项来控制模型复杂度，其中L1正则化倾向于产生稀疏解实现特征选择，L2正则化则使参数均匀缩小以提高模型稳定性。此外，Dropout作为一种有效的防过拟合策略，通过在训练过程中随机失活神经元，降低了模型对特定特征的依赖，并等效于进行模型平均，显著提升了模型的泛化能力。文章结合示意图和代码示例，直观地展示了这些概念和技术在实际应用中的效果。