当前位置：首页 > news >正文

7.3.折半查找(二分查找)

news 来源：原创 2025/6/12 21:48:42

一.折半查找(二分查找)的算法思想：

以上述图片为例，

有序："有序"指的是查找表中各个数据元素的关键字都必须是有序的，要么是递增排序，要么是递减排序
上述图片的查找表中数据元素的关键字是递增排序的
顺序表："顺序表"相当于一个数组，用于存放数据元素，0、1、2等就是顺序表的下标

二.折半查找(二分查找)算法的实例：

例一：查找成功

以上述图片的顺序表为例，该顺序表中的数据元素是按照递增排序的，

假设要在上述图片中的顺序表里查找关键字33，

首先需要定义low指针和high指针来确定目前要搜索的区间，

low指针初始指向顺序表的第一个位置即0索引上，

high指针初始指向顺序表的最后一个位置即顺序表的长度减1索引上，

本例中low指针指向0索引，high指针指向TableLen-1索引，

还需要定义一个mid指针用来指向low指针和high确定的区间的中间的元素，

mid指针的计算公式为mid = ( low + high ) / 2，

如下图：

如上图，进行第一轮的查找，

第一轮中low指针指向顺序表0索引的位置，high指针指向顺序表10索引的位置（因为此时顺序表的长度为11），

通过mid = ( low + high ) / 2可知mid指针指向顺序表5索引的位置，

因此第一轮要检查的元素是5索引上的元素即29，

把此时mid指针所指向的元素29和目标关键字33进行对比，会发现目标关键字33大于当前mid指针所指向的元素29，

所以如果33在顺序表中的话，那么只可能是在mid指针所指位置的右边区域（因为该顺序表中的数据元素是按照递增排序的），也就是顺序表中6索引到10索引的范围，

而对于mid指针所指位置的左边区域中的所有数据元素都是比mid指针指向的29要小的，是不可能存在33的，因此可以把mid指针所指位置的左边区域的元素都排除掉

（所以这就是为什么叫折半查找/二分查找，因为当前检查的元素是mid指针所指向的元素，该元素把当前搜索范围一分为二，分为了左区间和右区间，判断目标关键字和当前mid指针所指向的元素的大小关系，就可以知道下一步应该是在左区间还是右区间查找），

现在可以确定目标关键字只可能出现在mid指针所指位置的右边区域，因此要把low指针指向顺序表中6索引的位置即mid指针所指向的位置加1，high指针指向的位置不变即high指针指向顺序表10索引的位置，

这里mid指针所指向的元素29已经明确了与目标关键字33不相等，因此可以略过，

如下图：

如上图，进行第二轮的查找，

第二轮中low指针指向顺序表6索引的位置，high指针指向顺序表10索引的位置，

通过mid = ( low + high ) / 2可知mid指针指向顺序表8索引的位置，

因此第二轮要检查的元素是8索引上的元素即37，

把此时mid指针所指向的元素37和目标关键字33进行对比，会发现目标关键字33小于当前mid指针所指向的元素37，

所以如果33在顺序表中的话，那么只可能是在mid指针所指位置的左边区域（因为该顺序表中的数据元素是按照递增排序的），也就是顺序表中6索引到7索引的范围，

而对于mid指针所指位置的右边区域中的所有数据元素都是比mid指针指向的37要大的，是不可能存在33的，因此可以把mid指针所指位置的右边区域的元素都排除掉，

现在可以确定目标关键字只可能出现在mid指针所指位置的左边区域，因此要把high指针指向顺序表中7索引的位置即mid指针所指向的位置减1，low指针指向的位置不变即low指针指向顺序表6索引的位置，

这里mid指针所指向的元素37已经明确了与目标关键字33不相等，因此可以略过，

如下图：

如上图，进行第三轮的查找，

第三轮中low指针指向顺序表6索引的位置，high指针指向顺序表7索引的位置，

通过mid = ( low + high ) / 2可知mid指针指向顺序表6索引的位置（注：除不尽时C语言是向下取整），

因此第三轮要检查的元素是6索引上的元素即32，

把此时mid指针所指向的元素32和目标关键字33进行对比，会发现目标关键字33大于当前mid指针所指向的元素32，

所以如果33在顺序表中的话，那么只可能是在mid指针所指位置的右边区域（因为该顺序表中的数据元素是按照递增排序的），也就是顺序表中7索引的位置，

而对于mid指针所指位置的左边区域中的所有数据元素都是比mid指针指向的32要小的，是不可能存在33的，因此可以把mid指针所指位置的左边区域的元素都排除掉，

现在可以确定目标关键字只可能出现在mid指针所指位置的右边区域，因此要把low指针指向顺序表中7索引的位置即mid指针所指向的位置加1，high指针指向的位置不变即high指针指向顺序表7索引的位置，

这里mid指针所指向的元素32已经明确了与目标关键字33不相等，因此可以略过，

如下图：

如上图，进行第四轮的查找，

第四轮中low指针指向顺序表7索引的位置，high指针指向顺序表7索引的位置，

通过mid = ( low + high ) / 2可知mid指针指向顺序表7索引的位置，

因此第四轮要检查的元素是7索引上的元素即33，

把此时mid指针所指向的元素33和目标关键字33进行对比，会发现目标关键字33等于当前mid指针所指向的元素33，

因此查找成功。

例二：查找失败

以上述图片的顺序表为例，该顺序表中的数据元素是按照递增排序的，

假设要在上述图片中的顺序表里查找关键字12，

首先需要定义low指针和high指针来确定目前要搜索的区间，

low指针初始指向顺序表的第一个位置即0索引上，

high指针初始指向顺序表的最后一个位置即顺序表的长度减1索引上，

本例中low指针指向0索引，high指针指向TableLen-1索引，

还需要定义一个mid指针用来指向low指针和high确定的区间的中间的元素，

mid指针的计算公式为mid = ( low + high ) / 2，

如下图：

如上图，进行第一轮的查找，

第一轮中low指针指向顺序表0索引的位置，high指针指向顺序表10索引的位置（因为此时顺序表的长度为11），

通过mid = ( low + high ) / 2可知mid指针指向顺序表5索引的位置，

因此第一轮要检查的元素是5索引上的元素即29，

把此时mid指针所指向的元素29和目标关键字33进行对比，会发现目标关键字12小于当前mid指针所指向的元素29，

所以如果12在顺序表中的话，那么只可能是在mid指针所指位置的左边区域（因为该顺序表中的数据元素是按照递增排序的），也就是顺序表中0索引到4索引的范围，

而对于mid指针所指位置的右边区域中的所有数据元素都是比mid指针指向的29要大的，是不可能存在12的，因此可以把mid指针所指位置的右边区域的元素都排除掉

现在可以确定目标关键字只可能出现在mid指针所指位置的左边区域，因此要把high指针指向顺序表中4索引的位置即mid指针所指向的位置减1，low指针指向的位置不变即low指针指向顺序表0索引的位置，

这里mid指针所指向的元素29已经明确了与目标关键字12不相等，因此可以略过，

如下图：

如上图，进行第二轮的查找，

第二轮中low指针指向顺序表0索引的位置，high指针指向顺序表4索引的位置，

通过mid = ( low + high ) / 2可知mid指针指向顺序表2索引的位置，

因此第二轮要检查的元素是2索引上的元素即13，

把此时mid指针所指向的元素13和目标关键字12进行对比，会发现目标关键字12小于当前mid指针所指向的元素13，

所以如果12在顺序表中的话，那么只可能是在mid指针所指位置的左边区域（因为该顺序表中的数据元素是按照递增排序的），也就是顺序表中0索引到1索引的范围，

而对于mid指针所指位置的右边区域中的所有数据元素都是比mid指针指向的13要大的，是不可能存在12的，因此可以把mid指针所指位置的右边区域的元素都排除掉，

现在可以确定目标关键字只可能出现在mid指针所指位置的左边区域，因此要把high指针指向顺序表中1索引的位置即mid指针所指向的位置减1，low指针指向的位置不变即low指针指向顺序表0索引的位置，

这里mid指针所指向的元素13已经明确了与目标关键字12不相等，因此可以略过，

如下图：

如上图，进行第三轮的查找，

第三轮中low指针指向顺序表0索引的位置，high指针指向顺序表1索引的位置，

通过mid = ( low + high ) / 2可知mid指针指向顺序表0索引的位置（注：除不尽时C语言是向下取整），

因此第三轮要检查的元素是0索引上的元素即7，

把此时mid指针所指向的元素7和目标关键字12进行对比，会发现目标关键字12大于当前mid指针所指向的元素7，

所以如果12在顺序表中的话，那么只可能是在mid指针所指位置的右边区域（因为该顺序表中的数据元素是按照递增排序的），也就是顺序表中1索引的位置，

mid指针所指位置的左边区域此时不存在，

现在可以确定目标关键字只可能出现在mid指针所指位置的右边区域，因此要把low指针指向顺序表中1索引的位置即mid指针所指向的位置加1，high指针指向的位置不变即high指针指向顺序表1索引的位置，

这里mid指针所指向的元素7已经明确了与目标关键字12不相等，因此可以略过，

如下图：

如上图，进行第四轮的查找，

第四轮中low指针指向顺序表1索引的位置，high指针指向顺序表1索引的位置，

通过mid = ( low + high ) / 2可知mid指针指向顺序表1索引的位置，

因此第四轮要检查的元素是1索引上的元素即10，

把此时mid指针所指向的元素10和目标关键字12进行对比，会发现目标关键字12大于当前mid指针所指向的元素10，

现在可以确定目标关键字只可能出现在mid指针所指位置的右边区域，因此要把low指针指向顺序表中2索引的位置即mid指针所指向的位置加1，high指针指向的位置不变即high指针指向顺序表1索引的位置，

此时low指针的值大于high指针的值，不符合实际要求，因为规定low指针指向的是整个查找区间的最左边，high指向的是整个查找区间的最右边，所以必须low<=high，而现在本应该在左边的low指针在查找区间的最右边即low>high，就说明查找失败，

如下图：

三.折半查找(二分查找)算法的代码实现：

1.代码：

上述图片的代码解读：

1.上述图片里折半查找(二分查找)的代码是基于查找表中的各个数据元素是按照升序排列的，如果各个数据元素是按照降序排列的只需要稍作修改（原理类似）；

2.对于SSTable结构体：

ElemType *elem中 *elem是动态数组基址，用于存储数据元素，ElemType是查找表中数据元素的类型，因题而异
int TableLen中TableLen是查找表的长度，int是查找表长度的类型
SSTable结构体就是查找表的数据结构（顺序表）

3.Binary_Search函数的返回值是int型，形参中SSTable L是查找表，ElemType key是要查找的关键字（ElemType 是要查找的关键字key的数据类型，因题而已）；

4.所需要用到的指针：

low指针初始指向顺序表的第一个位置即0索引上
high指针初始指向顺序表的最后一个位置即顺序表的长度减1索引上
mid指针用来指向low指针和high确定的区间的中间的元素，mid指针的计算公式为mid = ( low + high ) / 2

5.while循环的循环条件为low<=high即如果low指针的值小于等于high指针的值，那么就执行while循环；

6.每一轮的while循环都会检查low指针和high指针确定的区间的中间元素即mid指针所指向的元素，判断mid指针所指向的元素和目标关键字key的大小关系：

如果mid指针所指向的元素等于目标关键字key，那么就直接返回mid指针所指的位置，表示查找成功，Binary_Search函数结束
如果mid指针所指向的元素大于目标关键字key，由于查找表的各个数据元素是按照升序排列的，如果目标关键字key存在于查找表中，那么只可能出现在mid指针所指位置的左区间，因此low指针不变，把high指针赋值为mid-1（详情见"折半查找(二分查找)算法的实例"）
如果mid指针所指向的元素小于目标关键字key，由于查找表的各个数据元素是按照升序排列的，如果目标关键字key存在于查找表中，那么只可能出现在mid指针所指位置的右区间，因此high指针不变，把low指针赋值为mid+1（详情见"折半查找(二分查找)算法的实例"）

7.如果经过多轮的while循环之后，发现low指针的值大于high指针的值，那么就会跳出while循环并返回-1，表示查找失败；

8.至此，这就是为什么折半查找(二分查找)只适用于有序的顺序表或数组，因为用顺序表或数组的形式可以根据下标立即就找到中间元素的位置，如果查找表是链表的话，要找到链表的中间元素只能从头开始依次往后找，才能找到中间的位置（还要得知链表的长度），也就是说链表不具备随机存取的特性，所以折半查找(二分查找)这个算法是不可能基于链表来实现的。

2.查找效率分析：

定义low指针和high指针，规定low指针指向的是当前查找区间的最左边，high指向的是当前查找区间的最右边，

还需要定义mid指针指向当前查找区间的中间位置，其中mid = ( low + high ) / 2，mid指针指向的元素也是每一轮查找中要检查的元素，

如下图：

以上述图片为例，其中查找表的数据元素是按照升序排列的，

第一轮查找中查找区间就是整个查找表即[0,10]，因此low指针指向查找表的0索引处，high指针指向查找表的10索引处，

通过mid = ( low + high ) / 2可知mid指针指向查找表中5索引上的元素即29，所以第一轮查找中要检查的是29，

如果要查找的关键字等于29，那么只需要经过一轮的循环即可完成查找，且需要经过一次关键字的对比即Ci为1；

如果要查找的关键字小于29，那么下一轮查找中就需要检查mid指针所指向位置的左区间即[0,4]；

如果要查找的关键字大于29，那么下一轮查找中就需要检查mid指针所指向位置的右区间即[6,10]，

如下图：

如上图，假定要查找的关键字小于29，那么第二轮查找的查找区间为[0,4]；

第二轮查找中查找区间为[0,4]，因此low指针指向查找表的0索引处，high指针指向查找表的4索引处，

通过mid = ( low + high ) / 2可知mid指针指向查找表中2索引上的元素即13，所以第二轮查找中要检查的是13，

如果要查找的关键字等于13，那么只需要经过两轮的循环即可完成查找，且需要经过两次关键字的对比即Ci为2；

如果要查找的关键字小于13，那么下一轮查找中就需要检查mid指针所指向位置的左区间即[0,1]；

如果要查找的关键字大于13，那么下一轮查找中就需要检查mid指针所指向位置的右区间即[3,4]，

(如果要查找的关键字大于29原理类似)，如下图：

如上图，假定要查找的关键字大于13，那么第三轮查找的查找区间为[3,4]；

第三轮查找中查找区间为[3,4]，因此low指针指向查找表的3索引处，high指针指向查找表的4索引处，

通过mid = ( low + high ) / 2可知mid指针指向查找表中3索引上的元素即16，所以第三轮查找中要检查的是16，

如果要查找的关键字等于16，那么只需要经过三轮的循环即可完成查找，且需要经过三次关键字的对比即Ci为3；

如果要查找的关键字小于16，那么下一轮查找中就需要检查mid指针所指向位置的左区间即[3,2]，显然不对，查找失败；

如果要查找的关键字大于16，那么下一轮查找中就需要检查mid指针所指向位置的右区间即[4,4]即4索引上的元素，

上述图片中也展示了其他mid指针可能指向的元素，原理类似，

如下图：

如上图，假定要查找的关键字大于16，那么第四轮查找的查找区间为[4,4]；

第四轮查找中查找区间为[4,4]，因此low指针指向查找表的4索引处，high指针指向查找表的4索引处，

通过mid = ( low + high ) / 2可知mid指针指向查找表中4索引上的元素即19，所以第四轮查找中要检查的是19，

如果要查找的关键字等于19，那么只需要经过四轮的循环即可完成查找，且需要经过四次关键字的对比即Ci为4；

如果要查找的关键字小于19，那么下一轮查找中就需要检查mid指针所指向位置的左区间即[4,3]，显然不对，查找失败；

如果要查找的关键字大于16，那么下一轮查找中就需要检查mid指针所指向位置的右区间即[5,4]，显然不对，查找失败；

上述图片中也展示了其他mid指针可能指向的元素，原理类似。

3.查找判定树：

如上图，以上述图片的查找表为例，把该查找表转化为查找判定树如下：

如上图，

在查找成功的情况下，最多有可能进行4轮的查找，因为绿色圆形结点最多有4层；

在查找失败的情况下，要查找的关键字就会落在紫色方形结点的区间内，

通过查找判定树可以直观地求出折半查找(二分查找)的平均查找长度ASL。

4.平均查找长度ASL：

上述图片里的顺序表的查找判定树如下：

以上述图片的查找判定树为例->

查找成功的情况：

绿色圆形结点共11个即查找表中共有11个数据元素，假设每一个数据元素查找成功的概率相同，那么每一个数据元素的查找成功的概率Pi为1/11，

第一层的数据元素有29，第一层的每一个数据元素都只需要1次关键字的对比就可以找到，所以C1都为1，由于第一层共1个数据元素，所以查找成功的ASL的第一项为1 * ( P1 * C1 ) = 1 * ( 1/11 * 1 )；

第二层的数据元素有12、37，第二层的每一个数据元素都只需要2次关键字的对比就可以找到，所以C2都为2，由于第二层共2个数据元素，所以查找成功的ASL的第二项为2 * ( P2 * C2 ) = 2 * ( 1/11 * 2 )；

第三层的数据元素有7、16、32、41，第三层的每一个数据元素都只需要3次关键字的对比就可以找到，所以C3都为3，由于第三层共4个数据元素，所以查找成功的ASL的第三项为4 * ( P3 * C3 ) = 4 * ( 1/11 * 3 )；

第四层的数据元素有10、19、33、43，第四层的每一个数据元素都只需要4次关键字的对比就可以找到，所以C4都为4，由于第四层共4个数据元素，所以查找成功的ASL的第四项为4 * ( P4 * C4 ) = 4 * ( 1/11 * 4 )，

所以查找成功的ASL = 1 * ( 1/11 * 1 ) + 2 * ( 1/11 * 2 ) + 4 * ( 1/11 * 3 ) + 4 * ( 1/11 * 4 ) = ( 1 * 1 + 2 * 2 + 3 * 4 + 4 * 4 ) * 1/11 = 3。

查找失败的情况：

紫色方形结点共有12个，假设每一个数据元素查找失败的概率相同，那么每一个数据元素的查找失败的概率Pi为1/12，

第一、二、三层不存在紫色方形结点，因此第一、二、三层不存在查找失败的情况，

第四层有4个紫色方形结点，到达这4个紫色方形结点的任意一个都只需要3次关键字的对比，所以C4为3，所以查找失败的ASL的第一项为4 * ( P4 * C4 ) = 4 * ( 1/12 * 3 )；

第五层有8个紫色方形结点，到达这8个紫色方形结点的任意一个都只需要4次关键字的对比，所以C5为4，所以查找失败的ASL的第二项为8 * ( P5 * C5 ) = 8 * ( 1/12 * 4 )，

所以查找失败的ASL = 4 * ( 1/12 * 3 ) + 8 * ( 1/12 * 4 ) = ( 3 * 4 + 4 * 8 ) * 1/12 = 11/3。

四.折半查找(二分查找)的查找判定树的构造：

1.情况一：

以上述图片为例，

上述图片的顺序表中共有11个数据元素，也就是奇数个数据元素，

此时的查找区间为[0,10]，可知指向该区间的中间指针mid指向5索引上的数据元素29，

在刨除mid指针所指向的29之后，还剩下10个数据元素，也就是还剩下偶数个数据元素，

剩下的这偶数个数据元素刚好可以被平分为左右两个部分，左边5个数据元素，右边5个数据元素，如下图：

如上图，以第二层的左子树为例，

第二层的左子树中共有5个数据元素，也就是奇数个数据元素，

查找区间为[0,4]，可知指向该区间的中间指针mid指向2索引上的数据元素13，

在刨除mid指针所指向的13之后，还剩下4个数据元素，也就是还剩下偶数个数据元素，

剩下的这偶数个数据元素刚好可以被平分为左右两个部分，左边2个数据元素，右边2个数据元素，如下图：

如上图，接下来以此类推，就不演示了。

2.情况二：

以上述图片为例，

上述图片的顺序表中共有10个数据元素，也就是偶数个数据元素，

此时的查找区间为[0,9]，可知指向该区间的中间指针mid指向4索引上的数据元素19（C语言的/运算符得到的是商，类似自动向下取整），

在刨除mid指针所指向的19之后，还剩下9个数据元素，也就是还剩下奇数个数据元素，

剩下的这奇数个数据元素无法被平分，左边4个数据元素，右边5个数据元素，如下图：

如上图，

第二层的左子树要比右子树少一个数据元素。

以第二层的左子树为例，

第二层的左子树中共有4个数据元素，也就是奇数个数据元素，

查找区间为[0,3]，可知指向该区间的中间指针mid指向1索引上的数据元素10（C语言的/运算符得到的是商，类似自动向下取整），

在刨除mid指针所指向的10之后，还剩下3个数据元素，也就是还剩下奇数个数据元素，

剩下的这奇数个数据元素无法被平分，左边1个数据元素，右边2个数据元素；

以第二层的右子树为例，

第二层的右子树中共有5个数据元素，也就是奇数个数据元素，

查找区间为[5,9]，可知指向该区间的中间指针mid指向7索引上的数据元素33，

在刨除mid指针所指向的33之后，还剩下4个数据元素，也就是还剩下偶数个数据元素，

剩下的这偶数个数据元素刚好可以被平分为左右两个部分，左边2个数据元素，右边2个数据元素，如下图：

如上图，接下来以此类推，如下图：

3.结论1：在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）

4.练习：

如果顺序表中有1个数据元素，

那么该顺序表的查找判定树只会有1个结点，

最终查找判定树如下图：

如上图，

如果顺序表中有2个数据元素，

在以之前确定1号结点的情况下，开始确定2号结点的位置，

根据结论"在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）"可得，

如果2号结点在以1号结点为根结点的左子树，那么此时以1为根结点的左子树中就有1个结点，以1为根结点的右子树中就有0个结点，左子树的结点数比右子树的结点数多1个，不符合结论（舍）；

如果2号结点在以1号结点为根结点的右子树，那么此时以1为根结点的左子树中就有0个结点，以1为根结点的右子树中就有1个结点，左子树的结点数比右子树的结点数少1个，符合结论，

因此2号结点在以1号结点为根结点的右子树中，

最终查找判定树如下图：

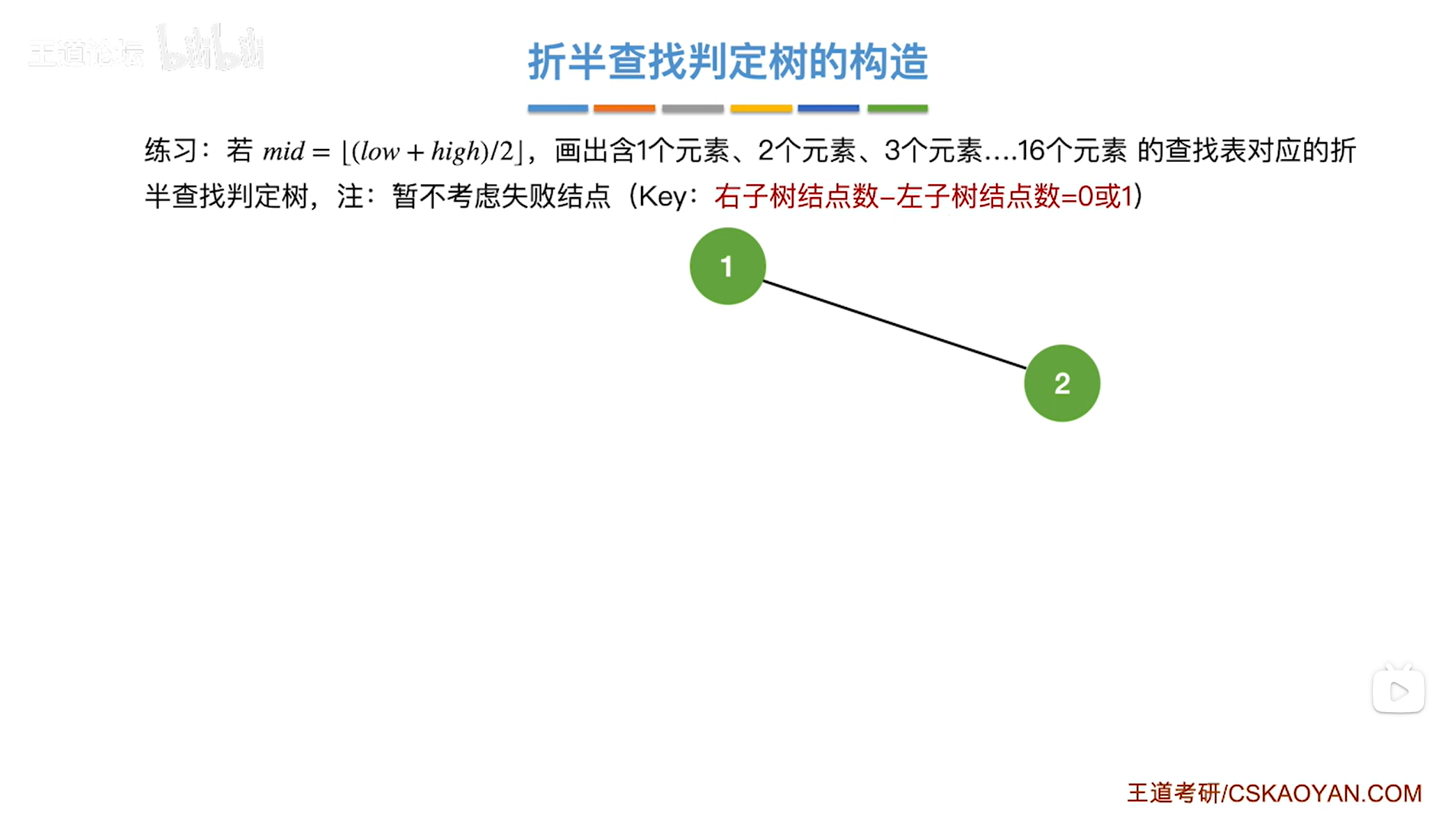
如上图，

如果顺序表中有3个数据元素，那么该顺序表的查找判定树不可能如下图：因为此时以1为根结点的右子树比左子树多2个结点，不符合结论，右子树的结点数最多比左子树的结点数多1个

如上图，

如果顺序表中有3个数据元素，

在以之前确定1、2号结点的情况下，开始确定3号结点的位置，

根据结论"在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）"可得，

如果3号结点在以1号结点为根结点的左子树，那么此时以1为根结点的左子树中就有1个结点，以1为根结点的右子树中就有1个结点，左子树的结点数等于右子树的结点数，符合结论；

如果3号结点在以1号结点为根结点的右子树，那么此时以1为根结点的左子树中就有0个结点，以1为根结点的右子树中就有2个结点，左子树的结点数比右子树的结点数少2个，不符合结论（舍），

因此3号结点在以1号结点为根结点的左子树中，

最终查找判定树如下图：

如上图，

如果顺序表中有4个数据元素，

在以之前确定1、2、3号结点的情况下，开始确定4号结点的位置，

根据结论"在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）"可得，

如果4号结点在以1号结点为根结点的左子树，那么此时以1为根结点的左子树中就有2个结点，以1为根结点的右子树中就有1个结点，左子树的结点数比右子树的结点数多1个，不符合结论（舍）；

如果4号结点在以1号结点为根结点的右子树，那么此时以1为根结点的左子树中就有1个结点，以1为根结点的右子树中就有2个结点，左子树的结点数比右子树的结点数少1个，符合结论，

因此4号结点在以1号结点为根结点的右子树中，

继续以2号结点作为根结点，判断4号结点应该在左子树还是右子树中，根据结论可知4号结点应该在以2号结点为根结点的右子树中，

最终查找判定树如下图：

如上图，

如果顺序表中有5个数据元素，

在以之前确定1、2、3、4号结点的情况下，开始确定5号结点的位置，

根据结论"在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）"可得，

如果5号结点在以1号结点为根结点的左子树，那么此时以1为根结点的左子树中就有2个结点，以1为根结点的右子树中就有2个结点，左子树的结点数等于右子树的结点数，符合结论；

如果5号结点在以1号结点为根结点的右子树，那么此时以1为根结点的左子树中就有1个结点，以1为根结点的右子树中就有3个结点，左子树的结点数比右子树的结点数少2个，不符合结论（舍），

因此5号结点在以1号结点为根结点的左子树中，

继续以3号结点作为根结点，判断5号结点应该在左子树还是右子树中，根据结论可知5号结点应该在以3号结点为根结点的右子树中，

最终查找判定树如下图：

如上图，

如果顺序表中有6个数据元素，

在以之前确定1、2、3、4、5号结点的情况下，开始确定6号结点的位置，

根据结论"在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）"可得，

如果6号结点在以1号结点为根结点的左子树，那么此时以1为根结点的左子树中就有3个结点，以1为根结点的右子树中就有2个结点，左子树的结点数比右子树的结点数多1个，不符合结论（舍）；

如果6号结点在以1号结点为根结点的右子树，那么此时以1为根结点的左子树中就有2个结点，以1为根结点的右子树中就有3个结点，左子树的结点数比右子树的结点数少1个，符合结论，

因此6号结点在以1号结点为根结点的右子树中，

继续以2号结点作为根结点，判断6号结点应该在左子树还是右子树中，根据结论可知6号结点应该在以2号结点为根结点的左子树中，

最终查找判定树如下图：

接下来以此类推：

所以无论顺序表中包含多少个数据元素，它所对应的折半查找的查找判定树一定是满足结论"在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）"，本例中给出的1、2、3...只是编号，不是关键字的值，如下图：

5.结论2：折半查找的查找判定树一定是平衡二叉树：

如上图，

任何一个顺序表的查找判定树中，任意一个结点的右子树和左子树的深度之差都不会超过1，

从刚才的推理过程可知折半查找的查找判定树只有最下面一层可能是不满的，

所以折半查找的查找判定树和完全二叉树一样，都是只有最下面一层可能是不满的，

因此如果折半查找的查找判定树中有n个结点，那么它的树高h的计算方法和完全二叉树的树高的计算方法是一样的（不考虑失败结点，如果包含失败结点，那么折半查找(二分查找)的树高h为h+1），如上图，本图给出h的计算方法是向上取整，详情见"5.4.二叉树的性质"。

6.失败结点的性质：

如上图，

在折半查找的查找判定树里，每一个结点里的关键字的值都符合"左子树的关键字的值<中间结点里的关键字的值<右子树的关键字的值"，

所以折半查找的查找判定树符合二叉排序树的定义；

任意一个结点的右子树和左子树的深度之差都不会超过1，

所以折半查找的查找判定树也符合平衡二叉树的定义；

假设顺序表中共有n个数据元素，

那么对应的查找判定树中共有n个结点，且有n个成功结点，有n+1个失败结点->证明如下：

法一：

在二叉树中只可能有度为0、度为1、度为2的三种结点，

设非空二叉树中

度为0的结点（叶子结点）总数为a，

度为1的结点总数为b，

度为2的结点总数为c，

失败结点只会连接在度为0的结点和度为1的结点上，而度为2的结点无法连接失败结点，因为度满了，

因此度为0的结点会连接2个失败结点，度为1的结点会连接1个失败结点，度为2的结点会连接0个失败结点，

假设失败结点共有m个，那么m = a * 2 + b * 1 + c * 0 = 2a + b，

假设二叉树中共有n个结点，那么就有n = a + b + c，n = b + 2c + 1（详情见"5.4.二叉树的性质"），

所以m + n = ( 2a + b ) + ( b + 2c + 1 ) = 2 * ( a + b + c ) + 1 = 2n + 1，所以m = n + 1。

法二：

在添加失败结点时，就是把失败结点连到各个结点的空链域上，因此失败结点的数量等于空链域的数量，

假设二叉树中共有n个结点，那么总共会有n+1个空链域（详情见"5.5.二叉树的存储结构"），

因此失败结点的数量为n+1个。

验证如下：如下图查找判定树中共有16个成功结点(绿色的圆形结点)，共有17个失败结点(紫色的方形结点)

五.折半查找(二分查找)的查找效率：

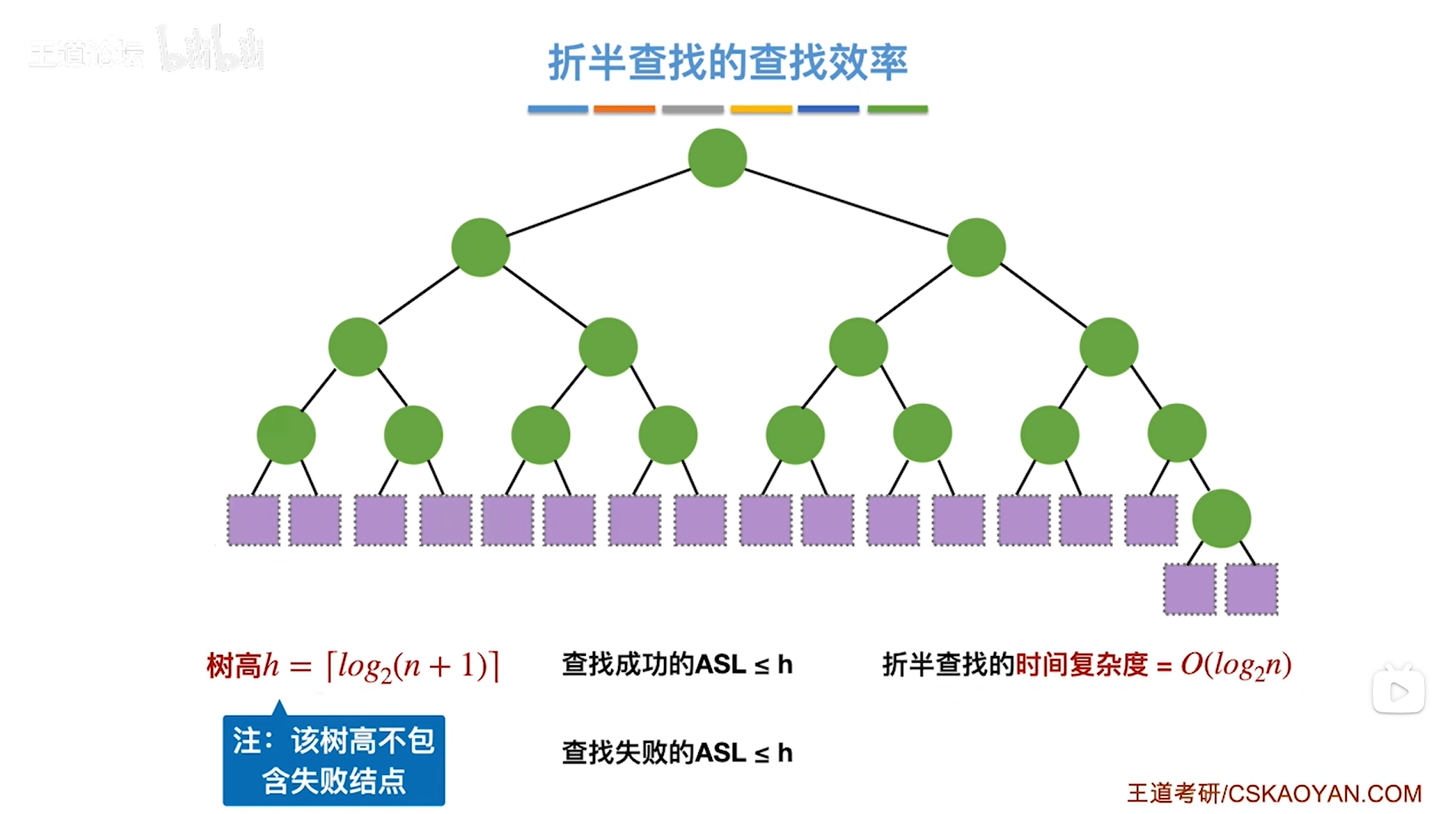
如上图，

折半查找的查找判定树的树高的计算方法和完全二叉树的树高的计算方法是一样的(本篇有推导)，详情见"5.4.二叉树的性质"。

假设一个顺序表中有n个数据元素，对于该顺序表的折半查找的查找判定树，如果不考虑失败结点的话，该查找判定树的高度h求法如上图，

在查找成功的情况下，查找到任何一个结点，总共需要的对比次数即ASL不会超过树高h，

在查找失败的情况下，所有的失败结点的关键字的对比次数也都不会超过树高h，

而树高h的数量级如上图，

因此折半查找的时间复杂度需要对比的次数的数量级如上图，

顺序查找的时间复杂度为O(n)（详情见"7.2.顺序查找"），

所以折半查找(二分查找)比顺序查找要高效（时间复杂度效率高低详情见"1.4.算法的时间复杂度"）。

六.总结：

对于一个折半查找，如果查找区间为[low,high]，中间指针mid = ( low + high ) / 2，且每次对比的是mid指针指向的数据元素，那么在查找判定树中对于任何一个结点都有"在同一个根结点下，右子树结点数-左子树结点数=0或1（右子树结点数不小于左子树结点数）"
如果包含失败结点，那么折半查找(二分查找)的树高h为h+1