Python训练营---DAY48
DAY 48 随机函数与广播机制
知识点回顾:
- 随机张量的生成:torch.randn函数
- 卷积和池化的计算公式(可以不掌握,会自动计算的)
- pytorch的广播机制:加法和乘法的广播机制
ps:numpy运算也有类似的广播机制,基本一致
作业:自己多借助ai举几个例子帮助自己理解即可
1、随机张量的生成:torch.randn函数
# 生成3维张量(常用于图像数据的通道、高度、宽度)
tensor_3d = torch.randn(3, 224, 224) # 3通道,高224,宽224
print(f"3维张量形状: {tensor_3d.shape}") # 输出: torch.Size([3, 224, 224])# 生成4维张量(常用于批量图像数据:[batch, channel, height, width])
tensor_4d = torch.randn(2, 3, 224, 224) # 批量大小为2,3通道,高224,宽224
print(f"4维张量形状: {tensor_4d.shape}") # 输出: torch.Size([2, 3, 224, 224])torch.rand():生成[0,1)范围内均匀分布的随机数
x = torch.rand(3, 2) # 生成3x2的张量
print(f"均匀分布随机数: {x}, 形状: {x.shape}")torch.randint():生成指定范围内的随机整数
x = torch.randint(low=0, high=10, size=(3,)) # 生成3个0到9之间的整数
print(f"随机整数: {x}, 形状: {x.shape}")torch.normal():生成指定均值和标准差的正态分布随机数。
mean = torch.tensor([0.0, 0.0])
std = torch.tensor([1.0, 2.0])
x = torch.normal(mean, std) # 生成两个正态分布随机数
print(f"正态分布随机数: {x}, 形状: {x.shape}")2、卷积和池化的计算公式(可以不掌握,会自动计算的)

3、pytorch的广播机制:加法和乘法的广播机制

案例 1:张量 a(3, 1) 与张量 b(3,)
- 步骤 1:补全维度
张量的形状可以理解为 “维度的元组”,为了对齐,先给维度少的张量补 1(在最左侧补) 。这里b原本是(3,)(1 维),补全后变成(1, 3)(2 维),和a的维度数(2 维)对齐。 - 步骤 2:逐维扩展
对每个维度,若其中一个张量该维度大小为1,就复制数据扩展到另一张量的维度大小 。a形状是(3, 1),b补全后是(1, 3):- 第 1 维(行方向):
a是3,b是1→b第 1 维扩展为3(复制自身 3 次)。 - 第 2 维(列方向):
a是1,b是3→a第 2 维扩展为3(复制自身 3 次)。
最终两者都扩展为(3, 3),就能逐元素运算。
- 第 1 维(行方向):
案例 2:张量 a(5, 1, 4) 与张量 b(1, 3, 1)
- 直接对比每个维度(从右往左):
- 第 3 维(最右侧):
a是4,b是1→ 兼容(1可扩展)。 - 第 2 维:
a是1,b是3→ 兼容(1可扩展)。 - 第 1 维:
a是5,b是1→ 兼容(1可扩展)。
- 第 3 维(最右侧):
- 扩展后,每个维度取较大值 :第 1 维
5、第 2 维3、第 3 维4,最终形状(5, 3, 4),满足广播。
案例 3:张量 a(2, 1, 3, 4) 与张量 b(5, 1, 4)
- 步骤 1:补全维度
b是 3 维,a是 4 维 → 给b最左侧补1,变成(1, 5, 1, 4),和a维度数(4 维)对齐。 - 步骤 2:逐维扩展
对比每个维度(从右往左):- 第 4 维:
a是4,b是4→ 相等,无需扩展。 - 第 3 维:
a是3,b是1→b第 3 维扩展为3(复制)。 - 第 2 维:
a是1,b是5→a第 2 维扩展为5(复制)。 - 第 1 维:
a是2,b是1→b第 1 维扩展为2(复制)。
最终形状(2, 5, 3, 4),完成广播。
- 第 4 维:
3.1加法的广播机制
二维+一维
import torch# 创建原始张量
a = torch.tensor([[10], [20], [30]]) # 形状: (3, 1)
b = torch.tensor([1, 2, 3]) # 形状: (3,)result = a + b
# 广播过程
# 1. b补全维度: (3,) → (1, 3)
# 2. a扩展列: (3, 1) → (3, 3)
# 3. b扩展行: (1, 3) → (3, 3)
# 最终形状: (3, 3)print("原始张量a:")
print(a)print("\n原始张量b:")
print(b)print("\n广播后a的值扩展:")
print(torch.tensor([[10, 10, 10],[20, 20, 20],[30, 30, 30]])) # 实际内存中未复制,仅逻辑上扩展print("\n广播后b的值扩展:")
print(torch.tensor([[1, 2, 3],[1, 2, 3],[1, 2, 3]])) # 实际内存中未复制,仅逻辑上扩展print("\n加法结果:")
print(result)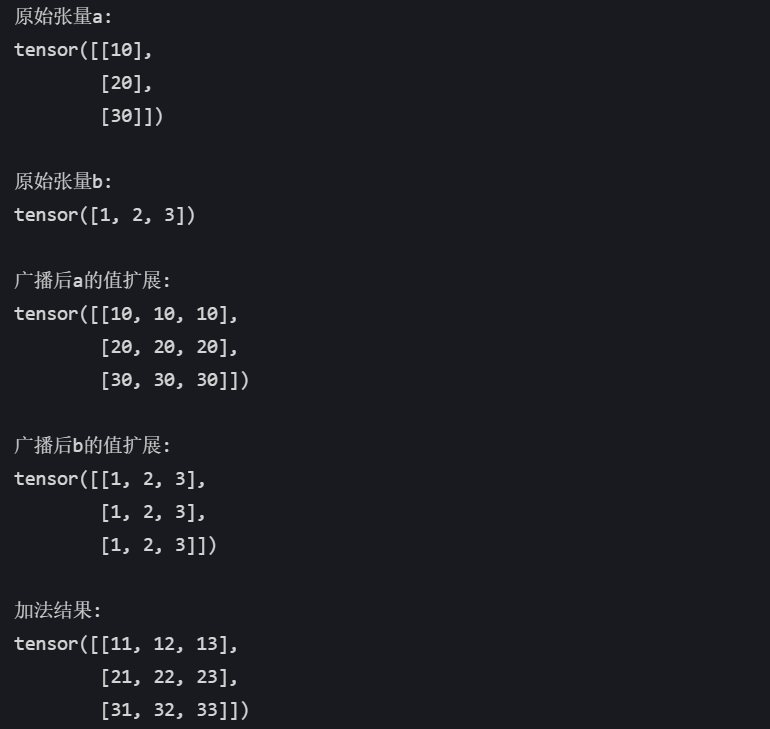
三维+二维
# 创建原始张量
a = torch.tensor([[[1], [2]], [[3], [4]]]) # 形状: (2, 2, 1)
b = torch.tensor([[10, 20]]) # 形状: (1, 2)# 广播过程
# 1. b补全维度: (1, 2) → (1, 1, 2)
# 2. a扩展第三维: (2, 2, 1) → (2, 2, 2)
# 3. b扩展第一维: (1, 1, 2) → (2, 1, 2)
# 4. b扩展第二维: (2, 1, 2) → (2, 2, 2)
# 最终形状: (2, 2, 2)result = a + b
print("原始张量a:")
print(a)print("\n原始张量b:")
print(b)print("\n广播后a的值扩展:")
print(torch.tensor([[[1, 1],[2, 2]],[[3, 3],[4, 4]]])) # 实际内存中未复制,仅逻辑上扩展print("\n广播后b的值扩展:")
print(torch.tensor([[[10, 20],[10, 20]],[[10, 20],[10, 20]]])) # 实际内存中未复制,仅逻辑上扩展print("\n加法结果:")
print(result)

二维+标量
# 创建原始张量
a = torch.tensor([[1, 2], [3, 4]]) # 形状: (2, 2)
b = 10 # 标量,形状视为 ()# 广播过程
# 1. b补全维度: () → (1, 1)
# 2. b扩展第一维: (1, 1) → (2, 1)
# 3. b扩展第二维: (2, 1) → (2, 2)
# 最终形状: (2, 2)result = a + b
print("原始张量a:")
print(a)
# 输出:
# tensor([[1, 2],
# [3, 4]])print("\n标量b:")
print(b)
# 输出: 10print("\n广播后b的值扩展:")
print(torch.tensor([[10, 10],[10, 10]])) # 实际内存中未复制,仅逻辑上扩展print("\n加法结果:")
print(result)
# 输出:
# tensor([[11, 12],
# [13, 14]])
3.2乘法的广播机制
批量矩阵与单个矩阵相乘
import torch# A: 批量大小为2,每个是3×4的矩阵
A = torch.randn(2, 3, 4) # 形状: (2, 3, 4)# B: 单个4×5的矩阵
B = torch.randn(4, 5) # 形状: (4, 5)# 广播过程:
# 1. B补全维度: (4, 5) → (1, 4, 5)
# 2. B扩展第一维: (1, 4, 5) → (2, 4, 5)
# 矩阵乘法: (2, 3, 4) @ (2, 4, 5) → (2, 3, 5)
result = A @ B # 结果形状: (2, 3, 5)print("A形状:", A.shape) # 输出: torch.Size([2, 3, 4])
print("B形状:", B.shape) # 输出: torch.Size([4, 5])
print("结果形状:", result.shape) # 输出: torch.Size([2, 3, 5])批量矩阵与批量矩阵相乘(部分广播)
# A: 批量大小为3,每个是2×4的矩阵
A = torch.randn(3, 2, 4) # 形状: (3, 2, 4)# B: 批量大小为1,每个是4×5的矩阵
B = torch.randn(1, 4, 5) # 形状: (1, 4, 5)# 广播过程:
# B扩展第一维: (1, 4, 5) → (3, 4, 5)
# 矩阵乘法: (3, 2, 4) @ (3, 4, 5) → (3, 2, 5)
result = A @ B # 结果形状: (3, 2, 5)print("A形状:", A.shape) # 输出: torch.Size([3, 2, 4])
print("B形状:", B.shape) # 输出: torch.Size([1, 4, 5])
print("结果形状:", result.shape) # 输出: torch.Size([3, 2, 5])三维张量与二维张量相乘(高维广播)
# A: 批量大小为2,通道数为3,每个是4×5的矩阵
A = torch.randn(2, 3, 4, 5) # 形状: (2, 3, 4, 5)# B: 单个5×6的矩阵
B = torch.randn(5, 6) # 形状: (5, 6)# 广播过程:
# 1. B补全维度: (5, 6) → (1, 1, 5, 6)
# 2. B扩展第一维: (1, 1, 5, 6) → (2, 1, 5, 6)
# 3. B扩展第二维: (2, 1, 5, 6) → (2, 3, 5, 6)
# 矩阵乘法: (2, 3, 4, 5) @ (2, 3, 5, 6) → (2, 3, 4, 6)
result = A @ B # 结果形状: (2, 3, 4, 6)print("A形状:", A.shape) # 输出: torch.Size([2, 3, 4, 5])
print("B形状:", B.shape) # 输出: torch.Size([5, 6])
print("结果形状:", result.shape) # 输出: torch.Size([2, 3, 4, 6])
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.dtcms.com/a/239364.html
如若内容造成侵权/违法违规/事实不符,请联系邮箱:809451989@qq.com进行投诉反馈,一经查实,立即删除!
