当前位置：首页 > news >正文

深究二分查找算法：从普通到进阶

news 来源：原创 2025/6/9 10:42:09

目录

前言

一、朴素版二分查找

1.题目引入

2.初次实践（暴力解法）

代码实现

3.二分算法

如何具体使用二分查找算法

细节问题

4.使用二分算法优化代码

代码实现

5.实践检验

代码实现

二、进阶版二分查找

1.题目引入

2.暴力破解

代码实现

3.进阶版二分查找

进阶二分原理

细节问题

4.使用进阶二分优化代码

代码实现

5.实践检验

代码实现

总结

前言

欢迎来到我的编程之路新系列——算法学习仓。在这里，我们将一起拆解那些历经时间考验、无处不在、威力巨大的核心算法。

本系列遵循由实践—理论—实践的过程，首先通过一些经典题型来认识、引出算法，然后再详细讲解该算法核心逻辑以及使用方法等，最后再回到实践中用该算法解决具体问题。

我们本次学习的算法是——经典的二分算法

一、朴素版二分查找

1.题目引入

题目链接：704. 二分查找 - 力扣（LeetCode）

题目描述：

这道题要求我们在一个升序数组中查找一个值t，若该值存在则返回他在数组的下标，不存在则返回-1。

2.初次实践（暴力解法）

拿到题一开始我们想的肯定是能否用暴力破解的方法解决该题，在已经有思路的情况下再设法使得该解法更加高效。

那么回到这道题，仔细观察题中示例，那么该题的暴力解法就已经呼之欲出了：

直接遍历整个数组，一个一个对比数组元素是否是目标值，若是则返回该元素下标；若遍历到数组末也没找到，则返回-1.

代码实现

int search(int* nums, int numsSize, int target) 
{for(int i=0;i<numsSize;++i){if(nums[i]==target)return i;}return -1;
}

时间复杂度分析

该算法最优情况下循环一次就能找到目标值；最坏情况下遍历完整个数组也没找到。

故暴力算法的时间复杂度是O(N)。

3.二分算法

上述暴力解法的时间复杂度为O(N)，让我们来思考如何优化暴力解法？

暴力解法慢就慢在：每次循环只能比较一个元素，最坏的情况下需要将整个数组都遍历一边，所以暴力解法的时间复杂度是O(N)。

优化思路：

在本题有一个规律我们没有用到，就是该数组是一个升序数组。

举个例子：我们有一个数组是[-1，0， 2， 3， 4， 5， 7， 9]，目标值 t = 5，如果一开始我们随便选择一个数就比如4。

同样的道理，如果选择7，那么包括7在内的后方一大批数都可以舍弃。

总结：在一个数组中随便找一个数，通过该数与目标值 t 做比较可将数组划分为两个区域，然后通过数组升序的规律我们可以舍弃一个区域，然后在另一个区域中寻找。

此时我们就称该数组具有“二分性”。如果一个数组具有二分性，那么便可通过二分查找算法高效解决。

什么是二分性？

二分性的本质是可以通过某个规律将数组划分为两个区域，并且根据规律能选择性的舍弃其中某个

区域，然后继续在另一个区域中查找。具有该种性质的问题就可以用二分查找算法解决。

将上述总结一下就能得到什么是二分算法了：

二分查找算法就是利用了数组的二分性，能够通过二分性将数组划分为两个区域，并能从中舍去一个区域，再到另一个区域中继续使用二分查找寻找目标值，直到找到目标值或者区域中元素为0——查完了没找到。

这里有一个问题：二分查找需要每次选定一个元素用来比较，那该怎样选择使得效率最高呢？

通过计算数学回归方程等方法证明，每次选取区域的中值元素可使的二分算法效率最大化。

如何具体使用二分查找算法

就拿上面的题目为例。

由于二分查找是需要在一个区域中进行，于是第一步：我们可以定义两个指针——left和right当作区域的左右下标，再用mid指针指向该区域的中间位置。

第二步：通过比较x与目标值t，得到下一次循环的区域范围，x与目标值无外乎三种情况：

细节问题

1.循环结束条件

当查找的区域范围变成0时，就应该结束循环。

也就是当left>right时循环应该结束。故循环的条件应该设为left<=right，一旦left>right立即结束循环。

2.二分算法为什么是正确的

二分算法能通过一次循环就排除一个区域，其本质是利用了二分性——发现的规律。就比如上述题目中的数组升序规律，只要排除了一个元素，那他之前比该元素小的肯定不可能是目标值。注意，这里博主强调的是二分性，而不是说数组有序！也就是说如果无序数组也能找到某种规律也是可以使用二分查找算法的。

3.二分查找算法的时间复杂度

二分查找时间复杂度为O(logN)，以2为底。计算过程如下：

4.使用二分算法优化代码

让我们再来看看这道题目描述：

算法解析

该题明确给出了给数组的特点——“升序”数组，使用朴素二分算法即可轻松解决。

代码实现

class Solution 
{
public:int search(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<=right){int mid=left+(right-left)/2;//等价于mid=（right-left）/2，预防溢出if(nums[mid]<target)left=mid+1;else if(nums[mid]>target)right=mid-1;else return mid;}return -1;}
};

对比时间复杂度

暴力解法O(N) VS 二分查找算法O(logN)

具体提升有多大呢？举个例子，假设该数组有2^30个元素，若用暴力算法则需要循环2^30次，而二分算法只需要循环30次！！

5.实践检验

题目链接：69. x 的平方根 - 力扣（LeetCode）

题目描述：

算法解析

该题的二段性在于，通过比较某数的平方与目标值的大小，可将数轴划分为两个区域。

该题的细节在于，若是某数无整数算术平方根，则取该数算数平方根相近的两个整数中较小的那一个数。

代码实现

class Solution {
public:int mySqrt(int x) {//if(x==0)return 0;long long left=0,right=x;while(left<=right){long long mid=left+(right-left)/2;long long sq=mid*mid;if(sq>x)right=mid-1;else if(sq<x)left=mid+1;else return (int)mid;}return left>right?(int)right:(int)left;}
};

二、进阶版二分查找

为什么还要了解进阶版得二分查找？原因是朴素二分不便解决一些区间类型问题，有的甚至失去二分查找优秀得时间复杂度。如下题。

1.题目引入

题目链接：34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题目描述：

2.暴力破解

直接遍历整个数组，一个一个对比数组元素是否是目标值。分别用两个变量记录其第一次与最后一次出现的数组下标。

代码实现

class Solution 
{
public:vector<int> searchRange(vector<int>& nums, int target) {int begin=-1,end=-1;for(int i=0;i<nums.size();++i){if(begin==-1&&nums[i]==target){end=begin=i;}if(end!=-1&&nums[i]==target){end=i;}}return {begin,end};}
};

时间复杂度

无论最优还是最次，时间复杂度都是O(N)。

3.进阶版二分查找

在考虑进阶版二分算法之前，我们先看看这道题能用朴素二分解决吗？

由于该题的特殊性，需要返回一段区间范围，若是用朴素二分也是可以做到，但时间复杂度却跌至O(N)——找到等于t的元素后，还需要往前往后遍历始终。特殊情况下若是整个数组元素都等于t，则需遍历完整个数组。

故该题不适合用朴素版二分查找解决。

进阶二分原理

依旧是拿上面的题目为例。

进阶二分查找是在朴素二分的基础之上进行的优化。

在上题中，由于需要返回两个值，而朴素二分只能查找到一个值，因此我们先尝试用朴素的二分找到找到其中一个端点，再用同样的方法找到另一个端点。

最后再来看看这里对朴素二分的优化在什么地方。

1）利用二分性找到左端点

2）利用二分性找到右端点

3）优化分析

相较于朴素二分查找，这里我们在利用二分性将数组分为两个区间时，就已经知道目标地址在的位置——在右区间的最左端，或左区间的最右端。由此，相较于朴素二分，在循环中的判断条件出现了改变。

找左端点时

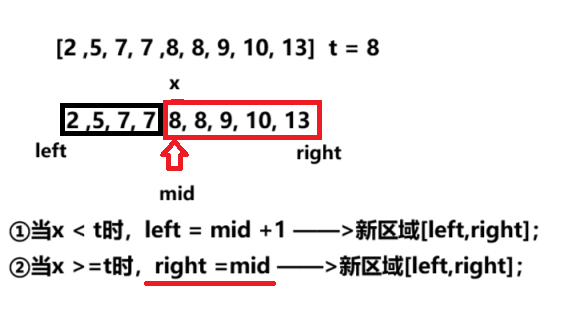
通过算法设计，我们已经知道了目标端点在区域中的位置，所以在循环中的任务是将区间正确的划分成两段。当left和right相遇时，就是目标在数组中的位置。

为什么right = mid 而不是mid -1？因为mid的位置有可能是最终结果，所以不能-1.

同理可得右端点

细节问题

1.循环结束的标志

当left==right时就找到了目标值的下标，所以循环条件应该是left < rigtht。

2.mid的取值

进阶版二分查找的mid取值十分关键！稍有不慎就会造成死循环，若是数组元素个数为奇数则不影响，若为偶数，由于mid的取值可能造成死循环。

具体来说：

1）当目标值在左区域的最右端时，mid = left +(right - left +1)/2。目的是当数组元素为偶数，且循环至最后两个元素时，使mid指向两个元素中靠右的值。因为此时剩下的两个元素各为一个区域，而目标是左区域的最右端的x，也就是说期望进行right = mid -1以达到left与right相遇终止循环。若是mid = left +(right - left )/2，则每次取得是靠左的元素x，由于x不满足使right-1的判断条件(x > t，因为x本就是目标端点x ==t)，则继续循环下去造成死机。

2）当目标值在右区域的最左端时，mid = left +(right - left )/2。理由同上，此时期望进行的是left = mid +1使得left与right相遇，终止进程。

若是读者觉得抽象可结合下方代码实现理解，进阶二分相较于普通二分查找抽象就在细节处理上，若还是有疑问请在评论区提出，笔者看到会第一时间解释。

4.使用进阶二分优化代码

题目内容：

算法解析

通过两次使用进阶二分查找，依次找到目标区间的起始地址和终止地址

代码实现

class Solution 
{
public:vector<int> searchRange(vector<int>& nums, int target) {size_t size=nums.size();int l=0,r=0;if(size==0)return {-1,-1};//找左int left=0,right=size-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target)left=mid+1;else if(nums[mid]>=target)right=mid;}//这里用于判断在数组中是否有目标值，若无直接return。if(nums[left]!=target)return {-1,-1};elsel=left;//找右left=0,right=size-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]<=target)left=mid;else if(nums[mid]>target)right=mid-1;}r=left;return {l,r};}
};

5.实践检验

能否利用进阶二分查找解决该问题呢？

题目链接：69. x 的平方根 - 力扣（LeetCode）

题目描述：

算法原理

利用二分性将数轴划分为两段，由题意得，若算术平方根非整数则返回左边区域的最右值。

代码实现

class Solution {
public:int mySqrt(int x) {if(x==0)return 0;size_t l=0,r=x;size_t mid=0;while(l<r){mid=l+(r-l+1)/2;size_t tmp=mid*mid;if(tmp>x)r=mid-1;else if(tmp<x)l=mid;else return mid;}//若算术平方根为整数则在whike中就已经return了，否则就是返回该值算术平方根左端的整数return l;}
};