计算机组成与体系结构：补码数制一（Complementary Number Systems）

目录

为什么需要补码数制？

什么是原码？

什么是反码？

 补码为什么被设计出来？

 补码是怎么做出来的？

什么是模运算？

为什么所有运算其实都是“模 2ⁿ”的运算？ 

1️⃣ 什么是补码？

2️⃣怎么快速求出 2ⁿ - x 呢？

为啥加这个补码就能完成减法？

---

为什么需要补码数制？

你可以想象一下，如果我们把一台计算机看作一个只会处理“二进制加法”的机器人，那它就不会直接做“减法”或“处理正负号”。那我们该怎么告诉这个机器人该怎么做呢？

这就需要一种“编码方法”，能：

• 表示正数和负数 

• 让机器人只用加法就能完成加法和减法 

• 还不容易出错 

这种方法，就是我们今天要学的 —— 补码数制（Two's Complement System）。

---

 我们学习补码数制的核心原因，是为了解决有符号数（Signed Numbers）在计算机中进行加减运算时所面临的表示和运算复杂性问题。

我们人类很容易分辨 +5 和 -5。可计算机内部只认得0 和 1，它怎么知道哪个数是正的、哪个是负的？

早期人们想了三种办法来解决：

方法	举例（以+5为例）	举例（以-5为例）	存在问题
原码（Sign-Magnitude）	00000101	10000101	有两个“0”（+0和-0），而且加减复杂
反码（Ones' Complement）	00000101	11111010	仍然有两个“0”，还要处理进位问题
补码（Two's Complement）	00000101	11111011	✅ 只有一个“0”，加法也能做减法！

所以，“补码”是三种方法中最优秀、最实用的一种。

什么是原码？

原码的思想非常简单：

最前面一位表示符号（Sign Bit），后面剩下的表示“数值大小”（Magnitude）

数值	原码（二进制）	说明
+5	00000101	符号位是 0，表示正数
-5	10000101	符号位是 1，表示负数，数值还是 5

✅ 特点：

• 人类容易理解（我们习惯于“+/-”）

• 正数和负数的数值部分是一样的

❌ 缺点：

• 存在两个“0”：+0 是 00000000，-0 是 10000000

• 加法、减法无法统一，只能通过判断符号、分情况计算

• 实现麻烦，尤其在硬件上（要分符号处理）

什么是反码？

 定义：

正数的反码 = 自身的二进制（和原码一样）
负数的反码 = 原码按位取反（0变1，1变0）

为什么要先发明反码？

反码是人类“用取反方式近似负数”的第一步尝试，但它仍然不完美（有两个零、进位问题），于是才改进成“补码”。

原码（Sign-Magnitude）：

• 虽然正负都能表示，但加减法必须判断符号、做特殊处理，复杂 ❌

所以人们想：

能不能想个方法，不管是加正数还是负数，都用一个“普通的二进制加法器”来搞定？

于是就有了“反码”：

负数 = 把正数按位取反

✅ 反码的特点：

• 对正数：反码和原码相同

• 对负数：按位取反

• 存在两个零：

  • 00000000（+0）

  • 11111111（-0）

❌ 反码的加法有问题：

举个例子：

+5 = 00000101  
-5 = 11111010（反码）  
相加：00000101 + 11111010 = 11111111 （这是 -0）

如果你想得到 0，你得“把最左边的进位再加回来”，这叫“尾进位回加（End-around carry）”。

这很麻烦，于是人们就设计了“补码”来解决这个问题。

补码和反码的关系：

补码 = 反码 + 1

🔍 本质原因：数学中的“模运算”告诉我们（下面会提到）：

 而如果你从反码的角度来看：

（因为 ~x 就是所有位取反，相当于 2ⁿ-1 - x）

那么：

 ✅ 正好得到了我们需要的补码形式！

所以“补码 = 反码 + 1”并不是人随便凑出来的，而是来自于数学上：

想要表达 -x = 2^n - x，而又不想每次手算 2^n - x，于是用“取反 + 1”作为快速计算方式。

---

 补码为什么被设计出来？

补码被设计出来，主要是为了解决以下两个问题：

✨ 问题1：怎么用同一个计算器完成加法和减法？

计算机的电路（比如加法器）本来只会做二进制加法（Binary Addition）。但现在你要让它“减”怎么办？

答案是：把“减法”变成“加法”！

7 - 5 = 7 + (-5)

如果你能找到一种方法，把 -5 表示成一种“特别的加数”，那减法也就变成加法了。

补码就是用来表示“负数”的那种特别编码方法，这样计算机只需要一个“加法器”就够了。

✨ 问题2：怎么让表示方式更统一、逻辑更清晰？

在原码或反码表示中：

• 有两个零（+0 和 -0）

• 比较、判断、计算都麻烦

但补码：

• 只用 00000000 表示 0

• 正数不用变，负数用一种规律取反加一的方式表示

• 数值范围对称，逻辑自然，硬件也更容易做出来

---

 补码是怎么做出来的？

原理背后：模（modulo）运算思想

什么是模运算？

🎯 定义：

模运算就是只保留“除以某个数后的余数”，也叫“取模”。

用数学语言说就是：

表达式	结果
7 mod 5	2
15 mod 8	7
-1 mod 8	7 （因为 -1 + 8 = 7）

模运算在补码系统中的应用

计算机中 n 位能表示的数有限，比如 8 位可以表示的总数是：

2 ^8 = 256

所以，在计算机里，所有运算其实都是“模 256”的运算，即：

为什么所有运算其实都是“模 2ⁿ”的运算？ 

💻 原因是：计算机能处理的数据是“位数有限”的

• 一个 8 位的 CPU 加法器，只能表示和处理 8 个比特（bit）

• 8 位能表示的范围是：从 0 到 255，总共 2⁸ = 256 个数

所以一切加法、减法、运算，最终都要“截断”到这 256 个数里。

 举个例子说明“模”的意义：

255 + 1 = 256 → 结果是 0（因为超出了范围，回到起点）

是不是像时钟？

• 12 点 + 3 小时 = 3 点（模 12）

• 255 + 1 = 0（模 256）

这就是“模运算”思想。

所以说：

在计算机中所有运算都是在 “模 2ⁿ” 的世界中进行的，因为数据位数是固定的。超出后就“回绕”或“溢出”了。

用术语说，这叫“模运算”，也叫“有限域计算”。

 那负数怎么办？

比如在 8 位二进制中，计算是模 256 的运算（也叫 模运算 Modulo Arithmetic）：

如果你想表示 -5，你就找一个数，使得：

而 251 的二进制就是： 

-5 的补码表示 = 251 = 11111011（二进制）

这正是 -5 的 补码表示！

所以： 

在 n 位二进制系统中，我们处理的数值其实是模 2^n 意义下的数。

✅ 关键：补码本质上就是用模 2^n 的“逆元”来表示负数

为什么 “取反 + 加1” 等价于模逆？

我们来从数学上拆解它：

1️⃣ 什么是补码？

假设我们有一个 4 位的系统（为了简单，不要一下就上 8 位） 

一共从 0 到 15，这就是“无符号数（Unsigned Number）”的范围。

但我们希望这4位可以同时表示正数和负数，怎么办？

问题来了：负数去哪儿了？

答案是：我们偷偷把后面一半的数字拿来表示负数！

也就是说：

二进制	实际代表的数（有符号）
0000	0
0001	+1
0010	+2
0011	+3
0100	+4
0101	+5
0110	+6
0111	+7
1000	-8 ⬅️ 从这里开始
1001	-7
1010	-6
1011	-5
1100	-4
1101	-3
1110	-2
1111	-1

你看：我们把“后面8个”二进制数，安排给了负数的补码表示。

负数应该对应哪个正数的“谁”？

我们来看看 -1 对应什么：

-1 的补码 = 1111
1111（四位） = 15（无符号），也就是 2⁴ - 1

所以你看出来了吧？

负数 x 的补码，其实就是 2ⁿ - |x|

所以：

• -1 的补码 = 2⁴ - 1 = 15 = 1111

• -5 的补码 = 2⁴ - 5 = 11 = 1011

所以补码是：

例如：在 8 位中，-5 的补码是：

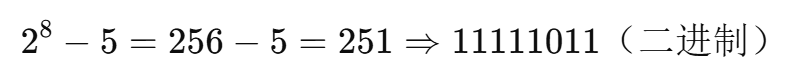
2️⃣怎么快速求出 2ⁿ - x 呢？

那我们能不能用一个“简单的方法”算出 251？

当然可以。看这个分步过程：

第一步：对正数 00000101 取反

得到：11111010 👉 相当于 ~x（按位取反）

第二步：加1

11111010 + 1 = 11111011

结果就是 256 - 5 = 251

所以“取反 + 加1”是一种快速求出 2^n - x 的方法！

这个值，正是 -x 在补码中的表示方式。

为啥加这个补码就能完成减法？

因为你做的是：

7 + (2^n - 5)

如果你是在 4 位的机器上，2ⁿ = 16，那：

7 + (16 - 5) = 7 + 11 = 18

但是，4 位机器只能保留最后 4 位（二进制）： 

18 = 10010 → 留最后 4 位：0010 = 2 ✅

你看到没有？

在限制位数的计算里（模 2ⁿ），加上负数的补码就等于减法

总结：“取反 + 加1”的设计原因

目的	为什么这么做？
✅ 统一加减法为加法	减法变成加上“负数补码”
✅ 用硬件实现简单	取反+加1可以用电路很快做出来
✅ 本质是模运算	2^n - x 就是负数在模系统中的等价表示
✅ 避免复杂进位逻辑	比如反码要尾加进位，补码不需要