当前位置：首页 > news >正文

动态规划熟悉30题 ---上

news 来源：原创 2025/6/7 8:10:24

本来是要写那个二维动态规划嘛，但是我今天在问题时候，一个大佬就把他初一时候教练让他练dp的30题发出来了（初一，啊虽然知道计算机这一专业，很多人从小就学了，但是我每次看到一些大佬从小学还是会很羡慕吧或者说一点点的崇拜，他们都好强，我也想这么强，但我是大一才开始了解，但我之后一定会变强的哈哈），然后说把这30题写完就差不多对dp熟悉一点点了，然后我就打算先写这30题的文章，之后再去写那个二维动态规划文章，，今天也听了几个大佬说，动态规划除了那些有天赋的人能几乎一眼看出某个比较难的题的dp数组含义还有他们的递推公式，其他人都是看题解去理解就好，不用为自己一直看不出来某个题烦，今天还刷到一个视频，是一个高中生妹妹在讲自己一天的经历，那个高中生妹妹好有活力哈哈，感觉很有精力，她说每天吃到好吃的东西也会很开心，还有谈恋爱，不一定要靠谈恋爱这个经历让自己开心，不要为了谈恋爱而谈恋爱，朋友也可以让自己很开心，一定要与自己和解，不要帮助别人一起欺负自己哈哈，话就说到这里哈，接下来我们开始做题，加油，一起变强

P1002 [NOIP 2002 普及组] 过河卒

P1002 [NOIP 2002 普及组] 过河卒 - 洛谷https://www.luogu.com.cn/problem/P1002

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0,0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1复制
6 6 3 3
输出 #1复制
6
说明/提示

对于 100% 的数据，1≤n,m≤20，0≤ 马的坐标 ≤20。

【题目来源】

NOIP 2002 普及组第四题

思路

这题我们可以很容易看出是类似于走楼梯是吧，我们走的格子是靠上，左这两个格子的状态得到的，

首先我们先定义dp数组，走到第i,j格子时候的路径数量,

然后我们找转移方程，题上说了卒只能向右和下走，这道题我们所定义的状态也就是格子，那我们所在的格子的状态是不是就是靠上和左这俩状态所转移，也就是相加。即dp[i][j]=dp[i-1][j]+dp[i][j-1]

接下来就看代码就好了，对了还有要对最开始的初始位置给初始化,dp[1][1]=1，因为自身就是一条路，所以最开始为1。注意开long long

#include<bits/stdc++.h>
using namespace std;
long long int dp[50][50];//到达i,j位置时的路径个数 
//存一下马能走的位置 
int mvx[]={-1,-2,-1,-2,1,2,1,2,0};
int mvy[]={-2,-1,2,1,2,1,-2,-1,0};
int main(){int n,m,x,y;cin>>n>>m>>x>>y;n++,m++,x++,y++;dp[1][1]=1;//这样就保证不用初始化了，后续循环从i=1,j=1开始 for(int i=0;i<=8;i++){int x1=x+mvx[i];int y1=y+mvy[i];if(x1>0&&y1>0) dp[x1][y1]=-1;//记录一下这些坐标不能走 } for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(i==1&&j==1) continue;if(dp[i][j]==-1){dp[i][j]=0;continue;}dp[i][j]=dp[i-1][j]+dp[i][j-1];}}cout<<dp[n][m]; 
}

P1044 [NOIP 2003 普及组] 栈

P1044 [NOIP 2003 普及组] 栈 - 洛谷https://www.luogu.com.cn/problem/P1044

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

宁宁考虑的是这样一个问题：一个操作数序列，1,2,…,n（图示为 1 到 3 的情况），栈 A 的深度大于 n。

现在可以进行两种操作，

将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

（原始状态如上图所示）

你的程序将对给定的 n，计算并输出由操作数序列 1,2,…,n 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 n（1≤n≤18）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

输入输出样例

输入 #1复制
3
输出 #1复制
5
说明/提示

【题目来源】

NOIP 2003 普及组第三题

思路

先说一下这是卡特兰数的用法，我就先说一下卡特兰数一半呢用到的地方在哪

卡特兰数简介

卡特兰数是一个经典的组合数学序列，常见于以下问题：

n个节点的二叉搜索树有多少种不同形态

包含n对括号的合法表达式有多少种

凸n+2边形的三角划分方案数

n个元素的出栈序列有多少种

分割问题为子问题：在 k 出栈之后，剩下的问题可以分为两个部分：左边的子问题：处理 1, 2, ....., k-1 的出栈序列。右边的子问题：处理 k+1, k+2, ...., n 的出栈序列。这两个子问题的解相互独立，并且可以组合起来形成原问题的解。

就是怎么说呢，因为入栈的序列是123456这种按顺序的，所以当元k素出栈，那一定还有n-k个元素没出栈对吧，也一定有k-1个元素已经出栈了，是吧，就是这样分割为子问题。

那我们要求n个元素的出栈顺序，他可以是 1或 2或3,....先出栈是吧，那是不是就变成求出n个不同元素先出栈之后的情况，

对于 dp[i] ，假设第一个出栈的元素是第 k 个入栈的元素（这里 k 从 1 到 i ）。那么在它出栈之前，有 k-1 个元素已经在它之前入栈并可能出栈，剩下的 i-k 个元素还没入栈。对于这 k-1 个元素来说，它们的合法出栈序列数量是 dp[k-1] ；对于剩下的 i-k 个元素，它们的合法出栈序列数量是 dp[i-k] 。因此，总的合法出栈序列数量就是所有可能的 k 对应的情况之和，即：

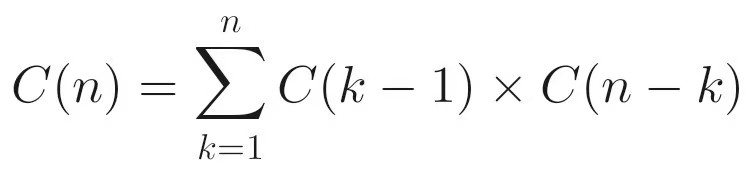
#include<bits/stdc++.h>
using namespace std;
int dp[20];
int n;
int main(){cin>>n;dp[0]=1;//空序列为出栈顺序是1dp[1]=1;//一个元素时候出栈顺序也为1for(int i=2;i<=n;i++){for(int k=1;k<=i;k++){dp[i]+=dp[i-k]*dp[k-1];}}cout<<dp[n];
}

P1057 [NOIP 2008 普及组] 传球游戏

P1057 [NOIP 2008 普及组] 传球游戏 - 洛谷https://www.luogu.com.cn/problem/P1057

题目描述

上体育课的时候，小蛮的老师经常带着同学们一起做游戏。这次，老师带着同学们一起做传球游戏。

游戏规则是这样的：n 个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师再次吹哨子时，传球停止，此时，拿着球没有传出去的那个同学就是败者，要给大家表演一个节目。

聪明的小蛮提出一个有趣的问题：有多少种不同的传球方法可以使得从小蛮手里开始传的球，传了 m 次以后，又回到小蛮手里。两种传球方法被视作不同的方法，当且仅当这两种方法中，接到球的同学按接球顺序组成的序列是不同的。比如有三个同学 1 号、2 号、3 号，并假设小蛮为 1 号，球传了 3 次回到小蛮手里的方式有 1→2→3→1 和 1→3→2→1，共 2 种。

输入格式

一行，有两个用空格隔开的整数 n,m(3≤n≤30,1≤m≤30)。

输出格式

1 个整数，表示符合题意的方法数。

输入输出样例

输入 #1复制
3 3
输出 #1复制
2
说明/提示

数据范围及约定

对于 40% 的数据，满足：3≤n≤30,1≤m≤20；
对于 100% 的数据，满足：3≤n≤30,1≤m≤30。

2008普及组第三题

思路

首先还是想怎么去定义dp数组，先看要求的东西，我们要求第m次传给第1个人的方法数，那很明显跟结果有关系的参数是啥，就是次数和第几个人，所以我们用二维数组来存储数据

再看每个人的来源都有啥是不是左边和右边人的传球，那这就是状态转移方程了，看代码

#include<bits/stdc++.h>
using namespace std;
int dp[50][50];
int n,m;
int main(){cin>>n>>m;dp[0][1]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){//向右传球if(j==n) dp[i][1]+=dp[i-1][j];else{dp[i][j+1]+=dp[i-1][j];}//向左传球if(j==1) dp[i][n]+=dp[i-1][j];else{dp[i][j-1]+=dp[i-1][j];}}}cout<<dp[m][1];
}

P1077 [NOIP 2012 普及组] 摆花

P1077 [NOIP 2012 普及组] 摆花 - 洛谷https://www.luogu.com.cn/problem/P1077

题目描述

小明的花店新开张，为了吸引顾客，他想在花店的门口摆上一排花，共 m 盆。通过调查顾客的喜好，小明列出了顾客最喜欢的 n 种花，从 1 到 n 标号。为了在门口展出更多种花，规定第 i 种花不能超过 ai 盆，摆花时同一种花放在一起，且不同种类的花需按标号的从小到大的顺序依次摆列。

试编程计算，一共有多少种不同的摆花方案。

输入格式

第一行包含两个正整数 n 和 m，中间用一个空格隔开。

第二行有 n 个整数，每两个整数之间用一个空格隔开，依次表示 a1,a2,⋯,an。

输出格式

一个整数，表示有多少种方案。注意：因为方案数可能很多，请输出方案数对 106+7 取模的结果。

输入输出样例

输入 #1复制运行
2 4
3 2
输出 #1复制运行
2
说明/提示

【数据范围】

对于 20% 数据，有 0<n≤8,0<m≤8,0≤ai≤8。

对于 50% 数据，有 0<n≤20,0<m≤20,0≤ai≤20。

对于 100% 数据，有 0<n≤100,0<m≤100,0≤ai≤100。

NOIP 2012 普及组第三题

思路

这是个多重背包问题，但是咱这里就不管他是啥问题，就一步一步来写呗

看题目要求啥，要求方案数，跟什么有关。题目说了能排m个花，然后又给了n个种类的花，那我们就可以得到参数是当前用的花的种类数量以及选的花的数量

然后我们要找递推公式题目给的有限制，一种花只能放a[i]个，所以我们要把每个花放多少个的情况都加起来，嘶我说不清楚我直接在注释那里加吧

#include<bits/stdc++.h>
using namespace std;
int dp[120][120];
int a[120];
int n,m;
int mod=1e6+7;
int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}dp[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){//j就是代表着当前放的花的总数为j时候，放第i种花的情况，不懂的话需要//仔细去分析多想一段时间就行，我想了有二十多分钟啊，唉我要是天才就好了for(int k=0;k<=min(j,a[i]);k++){(dp[i][j]+=dp[i-1][j-k])%=mod;}}}cout<<dp[n][m];
}

P1091 [NOIP 2004 提高组] 合唱队形

P1091 [NOIP 2004 提高组] 合唱队形 - 洛谷https://www.luogu.com.cn/problem/P1091

题目描述

n 位同学站成一排，音乐老师要请其中的 n−k 位同学出列，使得剩下的 k 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 k 位同学从左到右依次编号为 1,2, … ,k，他们的身高分别为 t1,t2, … ,tk，则他们的身高满足 t1<⋯<ti>ti+1> … >tk(1≤i≤k)。

你的任务是，已知所有 n 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入格式

共二行。

第一行是一个整数 n（2≤n≤100），表示同学的总数。

第二行有 n 个整数，用空格分隔，第 i 个整数 ti（130≤ti≤230）是第 i 位同学的身高（厘米）。

输出格式

一个整数，最少需要几位同学出列。

输入输出样例

输入 #1复制
8
186 186 150 200 160 130 197 220
输出 #1复制
4
说明/提示

对于 50% 的数据，保证有 n≤20。

对于全部的数据，保证有 n≤100。

思路

这是导弹拦截问题哈，那这个事让求两个拦截，就是求一下递增子序列和递减子序列，直接递增子序列是从第0个元素开始，递减是从第n-1开始这里要注意哦，看代码吧

#include<bits/stdc++.h>
using namespace std;
int n;
int a[110];
int dpu[110];//递增
int dpd[110];//递减
int main(){cin>>n;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<n;i++){dpu[i]=1;for(int j=0;j<i;j++){if(a[i]>a[j]) dpu[i]=max(dpu[i],dpu[j]+1);}}for(int i = n-1; i >= 0; i--) {dpd[i] = 1;  // 初始化为1（至少包含自己）for(int j = i+1; j < n; j++) {if(a[j] < a[i]) {  // 注意是a[j]<a[i]，因为是从i向后的下降序列dpd[i] = max(dpd[i], dpd[j] + 1);}}}int ans=-1;for(int i=0;i<n;i++){
//减去自身那个1ans=max(dpu[i]+dpd[i]-1,ans);}cout<<n-ans;
}

P1095 [NOIP 2007 普及组] 守望者的逃离

P1095 [NOIP 2007 普及组] 守望者的逃离 - 洛谷https://www.luogu.com.cn/problem/P1095

题目背景

NOIP2007 普及组 T3

题目描述

恶魔猎手尤迪安野心勃勃，他背叛了暗夜精灵，率领深藏在海底的娜迦族企图叛变。

守望者在与尤迪安的交锋中遭遇了围杀，被困在一个荒芜的大岛上。

为了杀死守望者，尤迪安开始对这个荒岛施咒，这座岛很快就会沉下去。到那时，岛上的所有人都会遇难。

守望者的跑步速度为 17m/s，以这样的速度是无法逃离荒岛的。庆幸的是守望者拥有闪烁法术，可在 1s 内移动 60m，不过每次使用闪烁法术都会消耗魔法值 10 点。守望者的魔法值恢复的速度为 4 点每秒，只有处在原地休息状态时才能恢复。

现在已知守望者的魔法初值 M，他所在的初始位置与岛的出口之间的距离 S，岛沉没的时间 T。你的任务是写一个程序帮助守望者计算如何在最短的时间内逃离荒岛，若不能逃出，则输出守望者在剩下的时间内能走的最远距离。

注意：守望者跑步、闪烁或休息活动均以秒为单位，且每次活动的持续时间为整数秒。距离的单位为米。

输入格式

输入数据共一行三个非负整数，分别表示 M，S，T。

输出格式

输出数据共两行。

第一行一个字符串 Yes 或 No，即守望者是否能逃离荒岛。

第二行包含一个整数。第一行为 Yes 时表示守望者逃离荒岛的最短时间；第一行为 No 时表示守望者能走的最远距离。

输入输出样例

输入 #1复制
39 200 4
输出 #1复制
No
197
输入 #2复制
36 255 10
输出 #2复制
Yes
6
说明/提示

对于 30% 的数据，1≤T≤10，1≤S≤100；

对于 50% 的数据，1≤T≤103，1≤S≤104；

对于 100% 的数据，1≤T≤3×105，0≤M≤103，1≤S≤108。

思路

就先贪一下嘛，先都选60，那个最快的，然后最后再去比较17那个，这个还是挺简单的，看代码应该就好哈

#include<bits/stdc++.h>
using namespace std;
int dp[300010];
int m,s,t;
int main(){cin>>m>>s>>t;for(int tt=1;tt<=t;tt++){if(m>=10){m-=10;dp[tt]=dp[tt-1]+60;}else{m+=4;dp[tt]=dp[tt-1];}}for(int i=1;i<=t;i++){dp[i]=max(dp[i],dp[i-1]+17);if(dp[i]>=s){printf("Yes\n%d\n",i);return 0;}}printf("No\n%d\n",dp[t]);return 0;
}

P1358 扑克牌

题目列表 - 洛谷 | 计算机科学教育新生态https://www.luogu.com.cn/problem/list?keyword=1358

题目描述

组合数学是数学的重要组成部分，是一门研究离散对象的科学，它主要研究满足一定条件的组态（也称组合模型）的存在、计数以及构造等方面的问题。组合数学的主要内容有组合计数、组合设计、组合矩阵、组合优化等。

随着计算机科学的日益发展，组合数学的重要性也日渐凸显，因为计算机科学的核心内容是使用算法处理离散数据。

今天我们来研究组合数学中的一个有趣的问题，也是一个简单的计数问题：

从一副含有 n 张的扑克牌(每张扑克牌都不相同)中，分给 m 个人，第 i 个人得到 ai 张牌，求一共有几种分法，这个数可能非常大，请输出此数模 10007 后的结果。

输入格式

第一行两个整数为 n,m。

第二行 m 个整数 ai。

输出格式

此数模 10007 后的结果。

输入输出样例

输入 #1复制
5 2
3 1
输出 #1复制
20
输入 #2复制
20 19
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
输出 #2复制
8707
说明/提示

对于 50% 的数据：ai=1。

对于 100% 的数据：1≤n≤104，1≤m≤100，0≤ai≤100。

思路

学大佬的话热知识杨辉三角可以处理组合数问题我们先搞个用dp数组构造个杨辉三角

我们知道一个数等于他上面数的加左上角的数也就是公式C(n, k) = C(n-1, k) + C(n-1, k-1)

边界条件处理

C(0,0) = 1：
- 0 个元素选 0 个元素的方案数为 1（空集）
C(n,0) = 1：
- 从任意 n 个元素中选 0 个元素的方案数总是 1

看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[110];
int dp[10010][110];
long long ans=1;
int main(){dp[0][0]=1;for(int i=1;i<=10000;i++){dp[i][0]=1;}for(int i=1;i<=10000;i++){for(int j=1;j<=min(i,100);j++){dp[i][j]=dp[i-1][j]+dp[i-1][j-1];dp[i][j]%=10007;}}cin>>n>>m;for(int i=0;i<m;i++){cin>>a[i];(ans*=1LL*dp[n][a[i]])%=10007;n-=a[i];}cout<<ans;}

P1439 【模板】最长公共子序列

P1439 【模板】最长公共子序列 - 洛谷https://www.luogu.com.cn/problem/P1439

题目描述

给出 1,2,…,n 的两个排列 P1 和 P2 ，求它们的最长公共子序列。

输入格式

第一行是一个数 n。

接下来两行，每行为 n 个数，为自然数 1,2,…,n 的一个排列。

输出格式

一个数，即最长公共子序列的长度。

输入输出样例

输入 #1复制
5 
3 2 1 4 5
1 2 3 4 5
输出 #1复制
3
说明/提示

对于 50% 的数据， n≤103；
对于 100% 的数据， n≤105。

思路

这题非常的妙啊，就是让我更加理解了一下dp吧，这题洛谷第一个题解文章写的确实很好很好，可以看看他的题解

Junior Dynamic Programming——动态规划初步·各种子序列问题 - 洛谷专栏

我也按照他的解法写一下吧

依旧先讲一下最长上升子序列

1，n^2做法

首先最初时候，最长递增子序列都是自己本身，长度也就是1，我们定义dp[i]就是以num[i]元素结尾0....i范围最长上升子序列，

然后，我们开始枚举i之前的元素j，判断当前i元素是否大于j，是的话就继承j的长度+1，否的话就不继承，（我觉得这个继承这个词用的很好很好，虽然这题不难，但确实一下就理解了），这个也是导弹拦截问题的写法（我上面写的也有），接下来看代码

#include<bits/stdc++.h>
using namespace std;
int dp[5010];
int n;
int a[5010];
int main(){cin>>n;for(int i=0;i<n;i++){cin>>a[i];dp[i]=1;}int ans=0;for(int i=0;i<n;i++){for(int j=0;j<i;j++){if(a[i]>a[j]) dp[i]=max(dp[j]+1,dp[i]);ans=max(ans,dp[i]);}}cout<<ans;
}

好我们开始讲重点优化，nlogn解法

我们这次dp数组，索引为子序列的长度，然后数值就是相同长度子序列的最小末尾，就比如长度都为2，序列1是1 4，序列2是2 3，那dp[2]就是3（懂了吧），就是这样子我们以最小末尾做值，我们就能更好的继承长度，更好的构造最长上升子序列了，

看代码

#include<bits/stdc++.h>
using namespace std;
int dp[5010];
int n;
int a[5010];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];dp[i]=0x7fffffff;}int len=1;dp[1]=a[1];for(int i=2;i<=n;i++){if(a[i]>dp[len]) dp[++len]=a[i];else{//找到第一个大于等于a[i]的位置，此时这个长度子序列的末尾就可改成更小的a[i]了int pos=lower_bound(dp+1,dp+len+1,a[i])-dp;dp[pos]=a[i];}}cout<<len;
}

接下来进入正题

依旧先n^2解法

思路就是，dp[i][j]含义是序列1从0....i,序列2从0...j这两个串的最长公共子序列长度多长

当for循环遍历到两个字符相同时候，就变成dp[i][j]=dp[i-1][j-1]+1，因为这俩相同我们就要找这俩字符之前的状态然后我们继承这个状态+1。如果两个字符不相同，dp[i][j]=max(dp[i-1][j],dp[i][j-1])。当不相同我们要继承的状态就不是两个字符之前的了，因为可能第i和j-1相同，也可能第i-1和j-1相同，所以我们要继承这两个状态最大的那个。看代码

但是这样会超时，只要是1e4--1e5就超时了，我们必须要优化

#include<bits/stdc++.h>
using namespace std;
int dp[1010][10010];
int n;
int a[10010];
int b[10100];
int main(){cin>>n;for(int i=0;i<n;i++) cin>>a[i];for(int i=0;i<n;i++) cin>>b[i];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(a[i-1]==b[j-1]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);else{dp[i][j]=max(dp[i][j-1],dp[i-1][j]);}}}cout<<dp[n][n];return 0;}

优化解法nlogn

思路就是，我没用map存序列1的字符的位置，然后再从map里找到对应序列2每个字符在序列1中的位置是多少，然后我们记录起来，找到这个记录起来的数组，最长上升子序列则就是他们的最长公共子序列，我们就完成了由LCS转化为LIS(这是因为题给的是n的全排列所以可以)

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n;
int a[N],b[N],mp[N],dp[N], pos[N];
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i],mp[a[i]]=i,dp[i]=0x7fffffff;for(int i=1;i<=n;i++) cin>>b[i],pos[i]=mp[b[i]];int len=1;dp[1]=pos[1];for(int i=2;i<=n;i++){if(pos[i]>dp[len]) dp[++len]=pos[i];else{int p=lower_bound(dp+1,dp+len+1,pos[i])-dp;dp[p]=pos[i];}}cout<<len;return 0;}

P1616 疯狂的采药

P1616 疯狂的采药 - 洛谷https://www.luogu.com.cn/problem/P1616

此题为纪念 LiYuxiang 而生。

题目描述

LiYuxiang 是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同种类的草药，采每一种都需要一些时间，每一种也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是 LiYuxiang，你能完成这个任务吗？

此题和原题的不同点：

1. 每种草药可以无限制地疯狂采摘。

2. 药的种类眼花缭乱，采药时间好长好长啊！师傅等得菊花都谢了！

输入格式

输入第一行有两个整数，分别代表总共能够用来采药的时间 t 和代表山洞里的草药的数目 m。

第 2 到第 (m+1) 行，每行两个整数，第 (i+1) 行的整数 ai,bi 分别表示采摘第 i 种草药的时间和该草药的价值。

输出格式

输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

输入输出样例

输入 #1复制运行
70 3
71 100
69 1
1 2
输出 #1复制运行
140
说明/提示

数据规模与约定

对于 30% 的数据，保证 m≤103 。
对于 100% 的数据，保证 1≤m≤104，1≤t≤107，且 1≤m×t≤107，1≤ai,bi≤104。

思路

这个是完全背包模板，我来说说我对完全背包的理解

题上说求的是可以采到的草药的最大值，也就是在t时间内采到的最大值，换到背包问题就是，这么大空间能存的最大价值嘛，那么我们的dp数组也就这样定义，

核心操作

我们就先遍历每个草药，再遍历时间的所有状态（也就是背包容量的所有情况）然后对每个草药进行操作（操作就是判断往里面装和不往里面装，因为是完全背包问题，所以每个物品都可以一直装），看看代码结合一下

#include<bits/stdc++.h>
using namespace std;
int m,t;
struct drug{
int time;
int value;
}a[10020];
long long int dp[10000020];
int main(){cin>>t>>m;for(int i=1;i<=m;i++){cin>>a[i].time>>a[i].value;}for(int i=1;i<=m;i++){for(int j=a[i].time;j<=t;j++){dp[j]=max(dp[j],dp[j-a[i].time]+a[i].value);}}cout<<dp[t];
}

P1679 神奇的四次方数

题目背景

在你的帮助下，v 神终于帮同学找到了最合适的大学，接下来就要通知同学了。在班级里负责联络网的是 dm 同学，于是 v 神便找到了 dm 同学，可 dm 同学正在忙于研究一道有趣的数学题，为了请 dm 出山，v 神只好请你帮忙解决这道题了。

题目描述

将一个整数 m 分解为 n 个四次方数的和的形式，要求 n 最小。例如，当 m=706 时，因为 706=54+34，所以有 n=2。可以证明此时 n 最小。

输入格式

一行，一个整数 m。

输出格式

一行，一个整数 n。

输入输出样例

输入 #1复制
706
输出 #1复制
2
说明/提

数据范围及约定

对于 30% 的数据，m≤5000；
对于 100% 的数据，m≤100,000。

思路

这题是完全背包问题，以前是求出来背包里面能放到最大价值，现在是求出放的最小数量，首页就是每个数的四次方是价值为1的物品，然后就往里放，然后还要把之前的max变成min

#include<bits/stdc++.h>
using namespace std;
int m;
int dp[100010],a[60];
int main(){cin>>m;memset(dp,0x7f,sizeof(dp));//背包的所有容量情况都初始化为很大的值for(int i=1;i<=50;i++){a[i]=i*i*i*i;}dp[0]=0;//最外层遍历要装的物品for(int i=1;i<=50;i++){//内层遍历背包容量for(int j=a[i];j<=m;j++){dp[j]=min(dp[j],dp[j-a[i]]+1);}}cout<<dp[m];
}

P1734 最大约数和

题目描述

选取和不超过 S 的若干个不同的正整数，使得所有数的约数（不含它本身）之和最大。

输入格式

输入一个正整数 S。

输出格式

输出最大的约数之和。

输入输出样例

输入 #1复制运行
11
输出 #1复制运行
9
说明/提示

【样例说明】

取数字 4 和 6，可以得到最大值 (1+2)+(1+2+3)=9。

【数据规模】

对于 100% 的数据，1≤S≤1000。

思路

这个是01背包问题，一个数只能放一个，我们先存一下物品，题上说选取若干个不超过s的正整数，题上还说约数（不含其本身），如果物品有1那就含其本身了，所以我没懂物品重量从2开始，s就是我们的背包容量，然后约数就是物品价值，就这样

因为01背包一个物品只能放一个，和完全背包区别就是01的内层循环是倒序，然后--就可以保证不会把一个物品多次放进去，好了看代码

#include<bits/stdc++.h>
using namespace std;
int s;
int a[1010];//需要放入背包的物品
int dp[1010];
int main(){cin>>s;//要从2开始for(int i=2;i<=s;i++){for(int j=1;j<i;j++){if(i%j==0){a[i]+=j;}}}//物品质量为i，价值为a[i]for(int i=2;i<=s;i++){for(int j=s;j>=i;j--){dp[j]=max(dp[j],dp[j-i]+a[i]);}}cout<<dp[s];
}

P2639 [USACO09OCT] Bessie's Weight Problem G

题目描述

Bessie 像她的诸多姊妹一样，因为从 Farmer John 的草地吃了太多美味的草而长出了太多的赘肉。所以 FJ 将她置于一个及其严格的节食计划之中。她每天不能吃多过 H(5≤H≤45,000) 公斤的干草。 Bessie 只能吃一整捆干草；当她开始吃一捆干草的之后就再也停不下来了。她有一个完整的N(1≤N≤500) 捆可以给她当作晚餐的干草的清单。她自然想要尽量吃到更多的干草。很自然地，每捆干草只能被吃一次（即使在列表中相同的重量可能出现2次，但是这表示的是两捆干草，其中每捆干草最多只能被吃掉一次）。给定一个列表表示每捆干草的重量 Si(1≤Si≤H) , 求 Bessie 不超过节食的限制的前提下可以吃掉多少干草（注意一旦她开始吃一捆干草就会把那一捆干草全部吃完）。

输入格式

第一行有两个由空格隔开的整数 H 和 N。

第 2 到第 N+1 行，第 i+1 行是一个单独的整数，表示第 i 捆干草的重量 Si。

输出格式

第一行一个单独的整数表示 Bessie 在限制范围内最多可以吃多少公斤的干草。

输入输出样例

输入 #1复制运行
56 4
15
19
20
21
输出 #1复制运行
56
说明/提示

输入说明

有四捆草，重量分别是 15,19,20 和 21。Bessie 在 56 公斤的限制范围内想要吃多少就可以吃多少。

输出说明

Bessie 可以吃 3 捆干草（重量分别为 15,20,21）。恰好达到她的 56 公斤的限制。

思路

01背包问题，重量和价值都是一样的其他的没啥了，就是个模板题

#include<bits/stdc++.h>
using namespace std;
int s;
int a[1010];//需要放入背包的物品
int dp[1010];
int main(){cin>>s;//要从2开始for(int i=2;i<=s;i++){for(int j=1;j<i;j++){if(i%j==0){a[i]+=j;}}}//物品质量为i，价值为a[i]for(int i=2;i<=s;i++){for(int j=s;j>=i;j--){dp[j]=max(dp[j],dp[j-i]+a[i]);}}cout<<dp[s];
}

P2008 大朋友的数字

P2008 大朋友的数字 - 洛谷https://www.luogu.com.cn/problem/P2008

题目背景

在 NOIP2013 的赛场上，常神牛华丽丽的手残了，小朋友的数字一题只得了 10 分。于是，他要恶搞一下这道题。

题目描述

有一批大朋友（年龄 15 岁以上），他们每人手上拿着一个数字，当然这个数字只有 1 位，也就是 0 到 9 之间。每个大朋友的分数为在他之前的最长不下降子序列中所有数之和。（这个序列必须以它作为结尾！）如有多个最长不下降子序列，那么取编号字典序最小的。现在告诉你有 n 个大朋友，以及他们各自的数字，请你求出他们每个人的分数。

输入格式

第一行，1 个数 n。

第二行，n 个数，分别表示每个人的数字。

输出格式

一行，n 个数，分别表示每个人的分数。

输入输出样例

输入 #1复制
5
1 2 5 3 4
输出 #1复制
1 3 8 6 10
输入 #2复制
5
1 7 5 9 6
输出 #2复制
1 8 6 17 12
说明/提示

【样例解释 1】

五个人分数分别为 (1),(1+2),(1+2+5),(1+2+3),(1+2+3+4)。

【样例解释 2】

五个人分数分别为 (1),(1+7),(1+5),(1+7+9) （还有一个 (1,5,9)），(1+5+6)。

【数据规模】

对于 50% 的数据，1≤n≤500；

对于 80% 的数据，1≤n≤103；

对于 100% 的数据，1≤n≤104。

思路

就是上面讲过的上升子序列再顺手记录个和就行，看代码吧，应该能看懂

#include<bits/stdc++.h>
using namespace std;
int n;
int a[10020];
int b[10010];
int dp[10020];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=1;dp[i]=a[i];}for(int i=1;i<=n;i++){for(int j=1;j<i;j++){if(a[i]>=a[j]){if(b[i]<b[j]+1) {b[i]=b[j]+1;dp[i]=dp[j]+a[i];}}}}for(int i=1;i<=n;i++) cout<<dp[i]<<' ';
}

P1853 投资的最大效益

题目背景

约翰先生获得了一大笔遗产，他暂时还用不上这一笔钱，他决定进行投资以获得更大的效益。银行工作人员向他提供了多种债券，每一种债券都能在固定的投资后，提供稳定的年利息。当然，每一种债券的投资额是不同的，一般来说，投资越大，收益也越大，而且，每一年还可以根据资金总额的增加，更换收益更大的债券。

题目描述

例如：有如下两种不同的债券：

投资额 4000，年利息 400；
投资额 3000，年利息 250。

初始时，有 10000 的总资产，可以投资两份债券 1 债券，一年获得 800 的利息；而投资一份债券 1 和两份债券 2，一年可获得 900 的利息，两年后，可获得 1800 的利息；而所有的资产达到 11800，然后将卖掉一份债券 2，换购债券 1，年利息可达到 1050；第三年后，总资产达到 12850，可以购买三份债券 1，年利息可达到 1200，第四年后，总资产可达到 14050。

现给定若干种债券、最初的总资产，帮助约翰先生计算，经过 n 年的投资，总资产的最大值。

输入格式

第一行为三个正整数 s,n,d，分别表示最初的总资产、年数和债券的种类。

接下来 d 行，每行表示一种债券，两个正整数 a,b 分别表示债券的投资额和年利息。

输出格式

仅一个整数，表示 n 年后的最大总资产。

输入输出样例

输入 #1复制运行
10000 4 2
4000 400
3000 250
输出 #1复制运行
14050
说明/提示

对于 100% 的数据，1≤s≤106，2≤n≤40，1≤d≤10，1≤a≤104，且 a 是 1000 的倍数，b 不超过 a 的 10%。

思路

就是完全背包，只是这题的背包容量会改，还有就是题上说a是1000倍数，我们要把重量都/1000，这样就不会RE了，其他都一样，看代码吧

#include<bits/stdc++.h>
using namespace std;
int s,n,d;//最初的总资产、年数和债券的种类。
int a[10020],b[10020];
int dp[10000010];
int main(){cin>>s>>n>>d;for(int i=1;i<=d;i++){cin>>a[i]>>b[i];}for(int k=1;k<=n;k++){int m=s/1000; for(int i=1;i<=d;i++){for(int j=a[i]/1000;j<=m;j++){dp[j]=max(dp[j],dp[j-a[i]/1000]+b[i]);}}  s+=dp[m];}cout<<s;}

总结

感觉学的还可以哈哈，可以的可以的，我上面写的如果有啥不懂的可以问哈（虽然应该没人看）