强化学习原理入门-2马尔科夫决策过程
2.1 马尔科夫决策过程理论讲解
强化学习的基本原理是:智能体和环境进行交互。
从强化学习的基本原理可以看出它与其他机器学习算法如监督学习和非监督学习的一些基本差别。在监督学习和非监督学习中,数据是静态的、不需要与环境进行交互,比如图像识别,只需要给出足够的差异样本,将数据输入深度网络中进行训练即可。然后,强化学习的学习过程是动态的、不断交互的过程,所需要的数据也是不断与环境进行交互的。所以,强化学习涉及的对象更多,比如动作、环境、状态状态概率和回报函数等。
强化学习更像是人的学习过程,人类通过与环境交互,学会走路、奔跑、劳动;人类与大自然,与宇宙的交互创造了现代文明。另外,深度学习如图像识别和语音识别解决的是感知问题,强化学习解决的是决策问题。
马尔科夫决策过程(MDP)是一套可以解决大部分强化学习问题的框架。
下面介绍 马尔科夫性-->马尔科夫过程-->马尔科夫决策。
1.马尔科夫性
指系统的下一个状态仅与当前状态
有关,而与以前的状态无关。
定义:状态是马尔科夫的,当且仅当
.
定义中可以看到,当前状态其实是蕴含了所有相关的历史信息
,一旦当前状态已知,历史信息将会被丢弃。
马尔科夫性描述的是每个状态的性质,但真正有用的是描述一个状态序列。数学中用来描述随机变量序列的学科叫随机过程。若随机变量序列中的每个状态都是马尔科夫的,则称此随机过程为马尔科夫随机过程。
2.马尔科夫过程
马尔科夫过程是一个二元组(S,P),且满足:S是有限状态集合,P是状态转移概率。状态转移概率矩阵为P
下面举一个列子进行阐述。
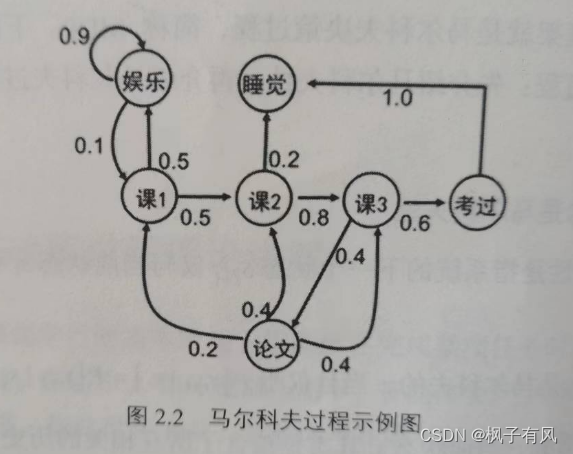
一个学生的7中状态{娱乐,课程1,课程2,课程3,考过,睡觉,论文}。一天可能的状态序列为:
课1-课2-课3-考过-睡觉
课1-课2-睡觉
以上状态序列成为马尔科夫链。当给定状态转移概率时,从某个状态出发存在多个马尔科夫链。对于游戏或机器人,马尔科夫过程不足以描述其特点,因为不管是游戏还是机器人,他们都是通过动作与环境进行交互,并从环境中获得奖励,而马尔科夫过程中不存在动作和奖励。将动作(策略)和回报考虑在内的马尔科夫过程称为马尔科夫决策过程。
3.马尔科夫决策过程
马尔科夫决策过程是由元组(S,A,P,R,)描述,其中
S 为有限的状态集
A 为有限的动作集
P 为状态转移概率
R 为回报函数
为折扣因子,用来计算累积回报。
跟马尔科夫过程不同的是,马尔科夫决策过程的状态转移概率是包含动作的,即

图2-3为马尔科夫决策过程的示例图,图2-3与图2-2相对应,在图2-3中,学生有五个状态,状态集S为{},动作集为A={玩,退出,学习,发表,睡觉},图2-3中,立即回报用R标记。
强化学习的目标是给定一个马尔科夫决策过程,寻找最优策略。所谓策略就是指状态到动作的映射,策略常用符号表示,它是指给定状态s时,动作集上的一个分布,即
(2.1)
这个公式中,策略的定义是用条件概率分布给出的。概率在强化学习中的重要作用,强化学习的策略往往是随机策略。采用随机策略的好处是可以将探索耦合到采样的过程中。所谓探索是指机器人尝试其他的动作以便找到更好的策略。其次,在实际应用中,存在各种噪声,这些噪声大都付出从正态分布,如何去掉噪声也用到概率的知识。
公式(2-1)的含义是:策略在每个状态s指定一个动作概率。如果给出的策略
是确定性的,那么策略
在每个状态s指定一个确定的动作。
例如一个学生的策略(玩|
)=0.8,是指该学生在状态s1时玩的概率为0.8,不玩的概率为0.2,显然这个学生更喜欢玩。
另一个学生的策略(玩|
)=0.3,是指该学生在状态s1时玩的概率为0.3,不玩的概率为0.7,显然这个学生不喜欢玩。
依次类推,每个学生都有自己的策略。强化学习是找到最优的策略,这里的最优是指得到的总回报最大。
当给定一个策略时,我们就可以计算累积回报了,首先定义累积回报:
 (2-2)
(2-2)
当给定义一个时,假设从状态
出发,学生状态序列可能为
s1->s2->s3->s4->s5
s1->s2->s3->s5
...
在策略下,利用公式2-2可以计算累积回报
,此时
有多个可能值。由于策略
是随机的,因此累积回报也是随机的。利用累积回报来衡量状态s1的价值。然而累积回报G1是个随机变量,不是确定的值,但其期望是确定的,可以作为状态值函数的定义。
(1)状态值函数
当智能体采用策略时,累积回报服从一个分布,累积回报在状态s处的期望值定义为状态-值函数。
 (2-3)
(2-3)
注意:状态值函数与策略是对应的,这是因为策略决定了累积回报G的状态分布.

图2.4中空心圆圈中的值为该状态的值函数,如=-2.3。
相应地,状态-行为值函数为
 (2-4)
(2-4)
公式2-3和公式2-4是定义计算式,但实际编程中并不按定义式。
(2)状态值函数与状态-行为值函数的贝尔曼方程。

同样,可以得到状态-动作值函数的贝尔曼方程。

具体推导过程这里省略,看原书P24-P26.
2.2 MDP中的概率学基础讲解
(1)随机变量
(2)概率分布
(3)条件概率
(4)期望和方差
(5)方差
最常用的概率分布也就是最常用的随机策略。
(1)贪婪策略
一个确定性策略,只有在使得动作值函数q*(s,a)最大的动作处取概率1,选其他动作的概率为0.
(2)-greedy策略
是强化学习最基本最常用的策略。
(3)高斯策略
高斯策略也平衡了利用和探索,其中利用由确定性部分完成,探索由完成。高斯策略在连续系统的强化学习中应广泛。
(4)玻尔兹曼分布
