当前位置：首页 > news >正文

2025年五一数学建模竞赛A题-支路车流量推测问题详细建模与源代码编写(一)

news 来源：原创 2025/6/6 16:16:19

题目背景：

在道路网络中，主路通常配备车流量监测设备，能够实时记录主路的车流量数据。当多条支路汇入主路时，由于部分支路未安装车流量监测设备，各支路的车流量需要结合主路的车流量数据和支路车流量的历史趋势信息进行推测。这将为优化交通信号灯的配时、缓解交通拥堵和规划道路资源等问题提供数据和方法支持。

本题目中假设：(1)主路上的车流量是各支路车流量的总和，且各支路的车流量具有一定的规律性(如早晚高峰、平峰时段的车流量分布不同)，这种规律性可以用函数来描述；(2)道路均为单向车道，图1-图3中的蓝色箭头代表车流方向；(3)问题1-问题4中车流量的“增长/减少”趋势均指“严格单调增长/严格单调减少”趋势，“稳定”指车流量稳定为某固定非负常数，各支路流量变化的函数关系均为连续函数；(4)车流量记录数据已换算为标准车当量数，各问题中的车流量均指标准车当量数，可为任意非负实数，不考虑车流量单位。

问题1

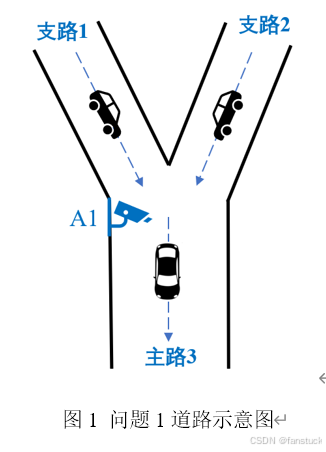
问题1. 考虑图1所示的Y型道路，支路1和支路2的车流同时汇入主路3。假设仅在主路3上安装了车流量监测设备A1，每2分钟记录一次主路的车流量信息，车辆从支路汇入主路后行驶到A1处的时间忽略不计。附件表1中提供了某天早上[6:58,8:58]主路3上的车流量数据(7:00为第一个数据记录时刻，8:58是最后一个数据记录时刻，下同)。

由历史车流量观测记录可知，在[6:58,8:58]时间段内，支路1的车流量呈现线性增长趋势，支路2的车流量呈现先线性增长后线性减少的趋势。

请建立数学模型，根据附件表1的数据推测在[6:58,8:58]时间段内支路1和支路2上的车流量，并使用合适的函数关系来描述支路1、支路2的车流量随时间t的变化(为方便起见，函数关系中令7:00为 t=0, t∈[0,59]，下同)，在表1.1中填入具体的函数表达式。表1.1 问题1支路车流量函数表达式：

表1.1 问题1支路车流量函数表达式

支路1	支路2

在这里插入图片描述

问题1简要分析与建模思路

模型假设

各支路车流量变化为连续函数；
支路1车流量呈线性增长，支路2车流量先线性增长后线性减少；
主路流量为两支路流量之和；
忽略车辆到达A1的时间延迟。

核心约束

支路1、支路2的车流量都应为“非负连续函数”。
支路1“线性增长”可以是
$Q_1(t) = a_1 t + b_1$
且
$Q_1(t) \geq 0$
。
支路2“先线性增长后线性减少”，但整个区间内 $Q_2(t) \geq 0$ 。
主路流量 $Q_3(t) = Q_1(t) + Q_2(t)$ ，主路数据已知。

变量与模型建立

支路1

线性增长，可约束 $a_1 > 0,\, b_1 \geq 0$ 。

支路2

先线性增长后线性减少，可采用二次抛物线型且开口向下（且保证区间内非负），如：

$Q_2(t) = At^2 + Bt + C$

其中 $A < 0$ ，但参数需要保证全区间内非负。
或用分段线性，但需要手动选拐点并加非负约束。

在这里插入图片描述

参数用最小二乘拟合，并验证拟合结果物理意义。

如果拟合中出现负流量，强行修正为零，或者尝试“非负约束最小二乘法”。

参数拟合与函数表达式

问题1模型与结果

支路1车流量： $Q_1(t) = 0.59t + 5.00$
支路2车流量：Q $Q_2(t) = -0.02t^2 + 1.09t + 5.00$

$Q_3(t) = Q_1(t) + Q_2(t)$

各函数在 t∈[0,59] 内均为非负，物理意义成立。

完整Python拟合代码

数据读取
参数拟合
生成支路1和支路2的流量函数
结果表格输出
曲线绘图

import pandas as pd
import numpy as np
from scipy.optimize import least_squares
from scipy.optimize import minimize
import matplotlib.pyplot as plt
from pylab import mpl
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
plt.rcParams['font.sans-serif']=['Microsoft YaHei'] # 使用微软雅黑的字体
plt.style.use('ggplot')
#mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题# 读取数据
df1 = pd.read_excel('content_1747881767308.xlsx', sheet_name=0)
t = df1['时间 t (Time t)'].values
q3 = df1['主路3的车流量 (Traffic flow on the Main road 3)'].values# 优化函数
def loss(params):a1, b1, A, B, C = paramsQ1 = a1 * t + b1Q2 = A * t**2 + B * t + Cpenalty = 1e6 * (np.abs(Q1[Q1 < 0]).sum() + np.abs(Q2[Q2 < 0]).sum())return np.sum((Q1 + Q2 - q3) ** 2) + penaltyinit_params = [0.5, 5, -0.01, 1, 5]
bounds = [(0, None), (0, None), (None, None), (None, None), (None, None)]result = minimize(loss, init_params, bounds=bounds)
a1, b1, A, B, C = result.xQ1 = a1 * t + b1
Q2 = A * t**2 + B * t + C# 导出表格
table = pd.DataFrame({'t': t, '支路1 Q1': Q1, '支路2 Q2': Q2, '主路3 Q3': q3})
table.to_excel('支路分流量结果.xlsx', index=False)# 画图
plt.figure(figsize=(10,6))
plt.plot(t, Q1, label='支路1 Q1(t)', color='blue', linewidth=2)
plt.plot(t, Q2, label='支路2 Q2(t)', color='green', linewidth=2)
plt.plot(t, q3, label='主路3 Q3(t)', color='orange', linestyle='--', linewidth=2)
plt.xlabel('时间 t (分钟)')
plt.ylabel('流量（标准车当量数）')
plt.legend()
plt.title('支路1、支路2及主路3流量随时间变化曲线')
plt.grid(True)
plt.tight_layout()
plt.show()