当前位置：首页 > news >正文

近端策略优化（PPO，Proximal Policy Optimization）

news 来源：原创 2025/6/6 19:16:24

OpenAI在2017年提出的强化学习算法，已成为深度强化学习的黄金标准，具有简单高效、稳定收敛等优势。

一解决的核心问题：策略更新不稳定

1.1策略更新不稳定

传统的策略梯度（PG）方法在一次策略梯度上升更新后，策略 $\pi_{\theta}$ 的参数 $\theta$ 发生了变化 -> 策略 $\pi_{\theta}$ 本身发生了改变 -> 用于估计梯度（依赖于当前策略下收集的经验）的数据来源于旧策略 $\pi_{\theta_{old}}$ ，策略更新后会导致数据分布改变。

1.2策略决定了轨迹分布

强化学习中，智能体在环境中行动。它在某个状态 s 时，根据其策略 $\pi_{\theta}(a|s)$ 选择一个动作 a。这个动作作用于环境，产生新状态 s' 和奖励 r ，如此往复，形成一条轨迹 (Trajectory)：τ = (s0, a0, r0, s1, a1, r1, ..., sT)。

个轨迹出现的概率分布完全由策略 $\pi_{\theta}$ 决定：

（1）初始状态由环境初始状态分布决定。

（2）动作由 $\pi_{\theta}(a_{0}|s_{0})$ 决定

（3）新状态由环境状态转移概率决定。

（4）后续的状态和动作同理，由决定。

策略 $\pi _{\theta }$ 参数化了整个轨迹出现的概率分布：

。

1.3策略参数更新意味着策略函数改变

略梯度方法的目的是优化策略参数 以最大化期望总奖励。

当我们执行一次梯度上升更新 $\theta_{new} = \theta_{old} + \alpha *\bigtriangledown \theta J(\theta)$ 后， $\theta _{new} \neq \theta _{old}$ 。

参数的变化必然导致策略函数的输出（即在每个状态下选择各个动作的概率）发生变化。

所以策略的改变直接导致整个轨迹的构成发生了根本性的变化。

二核心思想

2.1信任区域优化 (Trust Region Optimization)

（1）限制策略更新幅度，避免策略突变导致性能崩溃

（2）用数学约束确保新策略靠近旧策略

2.2Clipped Surrogate Objective (关键创新，核心组成部分)

2.2.1策略比率 (Probability Ratio)

公式：

$\pi _{\theta } \left ( a_{t} \mid s_{t}\right )$ ：新策略在状态下选择动作的概率。

$\pi _{\theta _{old}}\left ( a_{t} \mid s_{t}\right )$ ：生成这批经验数据的旧策略在状态下选择动作的概率（在收集经验时记录或存储的动作概率）。

$r_{t}(\theta )$ 衡量了新策略相对于旧策略，倾向于选择该历史动作的程度。

$r_{t}(\theta )$ ≈ 1：新策略和旧策略在这个状态动作对上的动作选择倾向类似。

$r_{t}(\theta )$ > 1：新策略比旧策略更倾向于选择该动作。

$r_{t}(\theta )$ < 1：新策略比旧策略更不倾向于选择该动作。

2.2.2优势函数 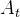(Advantage Function)

公式：

含义：评估在状态下选择动作比在状态下策略的平均表现好多少（或差多少）。是动作值函数（估计在执行后能获得的期望累积回报），是状态值函数（估计在下策略的平均期望累积回报）。

> 0：这个动作比平均动作好。

< 0：这个动作比平均动作差。

三 PPO裁剪目标函数

3.1未裁剪的目标函数

策略梯度的直觉： 最大化期望奖励。一个常见的代理目标函数（surrogate objective）是最大化 策略比率 * 优势函数 的期望:

$L\left ( \theta \right )=E_{t}\left [ r_{t}\left ( \theta \right )*A_{t} \right ]$

更新策略，使得在优势为正 ( > 0) 的动作上增加其被选择的概率 ( $r_{t}(\theta )$ > 1)。

在优势为负 ( < 0) 的动作上减少其被选择的概率 ( $r_{t}(\theta )$ < 1)。

问题： 直接最大化这个目标，当某个动作的为正且很大时，优化器可能会尝试将 $r_{t}(\theta )$ 变得非常大（即新策略极大地偏重这个动作），但这基于过时的旧策略数据，可能导致过大的策略改变，破坏策略的稳定性和性能。

3.2使用PPO裁剪代理目标函数

PPO 的核心创新在于修改了这个目标函数， 引入了裁剪操作以约束 $r_{t}(\theta )$ 的变化范围：

$L^{CLIP}(\theta ) = E_{t} \left [ min\left ( r_{t}\left ( \theta \right )*A_{t} ,clip\left ( r_{t}\left ( \theta \right ) ,1-\varepsilon ,1+\varepsilon \right )*A_{t}\right ) \right ]$

$min()$ ：最大化两个项中较小的那个。

$clip\left ( r_{t}\left ( \theta \right ) ,1-\varepsilon ,1+\varepsilon \right )$ ：将策略比率 $r_{t}(\theta )$ 强制限制在的范围内。

是一个小的超参数（如 0.1 或 0.2），定义了策略更新允许的幅度上限，确定了邻近优化区域的边界（proximal region）。

3.3裁剪目标函数的作用机制

3.3.1优势为正 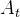`(` `> 0)` 时：

中的第一项： $r_{t}(\theta ) * A_{t}$

中的第二项： = 裁剪上限项

如果（新策略不过分偏向这个好动作），clip(...) 就是 $r_{t}(\theta )$ ，第二项等于第一项 $r_{t}(\theta ) * A_{t}$ 。

如果（新策略过分开心地选择这个好动作），clip(...) 就等于，第二项变成。

3.3.2优势为负 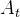`(` `< 0)` 时：

中的第一项： $r_{t}(\theta ) * A_{t}$ （因为 < 0，这是一个负值）。

中的第二项： = 裁剪下限项

如果（新策略未完全抛弃这个坏动作），clip(...) 就是 $r_{t}(\theta )$ ，第二项等于第一项 $r_{t}(\theta ) * A_{t}$ （负值）。

如果（新策略过激地惩罚这个坏动作），clip(...) 就等于，第二项变成 ，限制了对这个坏动作过度减少概率的幅度到 。

四 PPO优势和局限

4.1优势

（1）对超参数相对鲁棒：流行的关键原因之一

（2）实现简单：PPO-Clip 在标准的深度学习框架（PyTorch， TensorFlow）中实现起来非常直接。

（3）计算效率高（相比 TRPO）:PPO-Clip 使用一阶优化（SGD/Adam）处理约束，而 TRPO 的优化步骤需要计算二阶导数（Hessian矩阵）及进行共轭梯度/线性求解（或Fisher Vector Product），计算成本显著更高。

（4）表现优异（在广泛任务上）： 从 Atari 游戏到复杂的连续控制任务（如 MuJoCo， PyBullet）再到大规模语言模型微调（RLHF），PPO 是经过大量验证的 SOTA 策略梯度算法基准。

（5）支持多种策略类型： 能很好地应用于处理离散动作空间和连续动作空间的策略。

（6）强大的样本复用： K > 1 允许重复使用同一批数据更新 K 次，提高了样本效率（只要 K 设置合理）。

4.2局限

（1）样本效率仍有提升空间（与基于值的方法相比）： 与其他策略梯度方法一样，PPO 整体样本效率可能不如 DQN 或 RAINBOW 系列（纯粹基于值的方法）。训练过程需要相对较多的环境交互。

（2）Clip Epsilon 敏感： 在某些特别复杂或难优化的任务上，可能需要仔细微调的值才能达到最佳效果。

（3）离策略(off-policy)能力有限： PPO 本质上是在线策略(on-policy) 算法，因为更新主要依赖最近旧策略收集的数据。虽然 $r_{t}(\theta )$ 和 K Epochs 的使用体现了重要性采样的思想（近似 Off-policy 性质），但当新策略与生成数据的旧策略 $\pi _{\theta _{old}}$ 偏离较大（策略比率 $r_{t}(\theta )$ 剧烈变化或者被过度裁剪/惩罚）时，更新质量会迅速下降，即数据“过时”。因此不能很好地利用过旧的、策略相差甚远的数据。