SARIMA时间序列分析:三大模型对比
# 参考代码
d(x,1,12)
d(x,1,12) ma(1) sma(12)
d(x,1,12) ar(1) sma(12)
expand 1976M1 1977M12
6.1.1时序图

X t = T t × S t × I t X_t=T_t\times S_t\times I_t Xt=Tt×St×It
6.1.2 趋 势 效 应 T t 趋势效应T_t 趋势效应Tt

6.1.3 季 节 效 应 S t 季节效应S_t 季节效应St

6.1.4指数平滑法

X t = ( 893.128 + 1.583 t ) S j X_t = (893.128 +1.583t)S_j Xt=(893.128+1.583t)Sj

6.1.5 SARIMA模型建立
6.1.5.1 时序图差分 d ( x , 1 , 12 ) d(x,1,12) d(x,1,12)


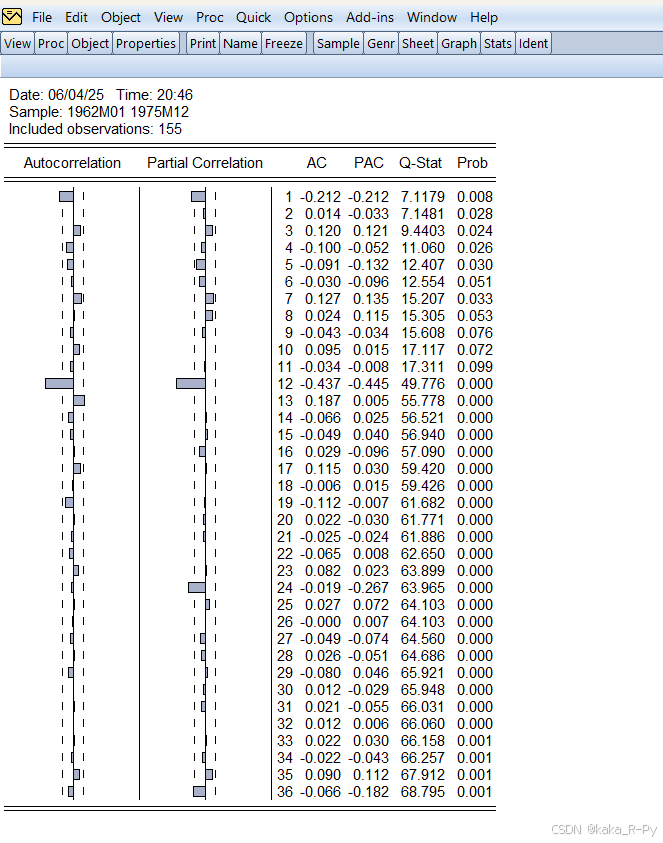
6.1.5.2 A R I M A ( 0 , 1 , 1 ) × ( 0 , 1 , 1 ) 12 ARIMA(0,1,1) \times (0,1,1)_{12} ARIMA(0,1,1)×(0,1,1)12

∇ 12 ∇ X t = ( 1 − 0.234 B ) × ( 1 − 0.704 B ) 12 ϵ t \nabla_{12} \nabla{X_t} =(1-0.234B)\times (1-0.704B)^{12}\epsilon_t ∇12∇Xt=(1−0.234B)×(1−0.704B)12ϵt





6.1.5.3 A R I M A ( 1 , 1 , 0 ) × ( 0 , 1 , 1 ) 12 ARIMA(1,1,0) \times (0,1,1)_{12} ARIMA(1,1,0)×(0,1,1)12
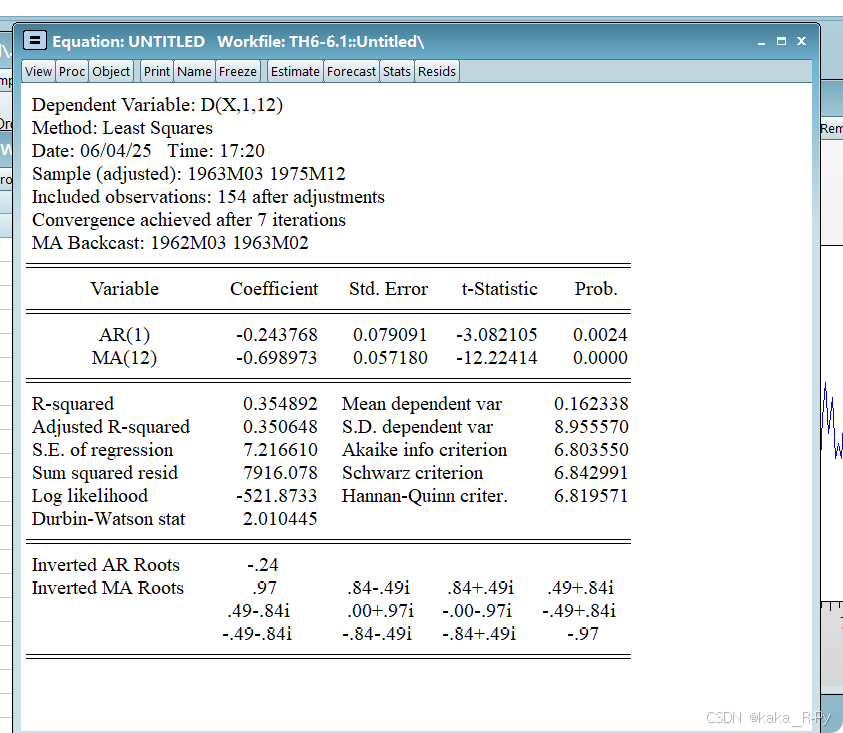
∇ 12 ∇ X t = 1 − 0.670 B 12 1 + 0.234 B ϵ t \nabla_{12} \nabla{X_t} =\frac{1-0.670B^{12}}{1+0.234B}\epsilon_t ∇12∇Xt=1+0.234B1−0.670B12ϵt





6.1.6拟合精度比较 R M S E RMSE RMSE
X t = T t × S t × I t X_t=T_t \times S_t \times I_t Xt=Tt×St×It
X t ^ = T t × S t = X t I t \hat{X_t}=T_t \times S_t =\frac{X_t}{I_t} Xt^=Tt×St=ItXt
M R S E = ∑ i = 1 m ( X i − X ^ i ) 2 m = ∑ i = 1 m ( X i − X i / I i ) 2 m MRSE=\sqrt{\frac{\sum_{i=1}^m\left(X_i-\hat{X}_i\right)^2}{m}}=\sqrt{\frac{\sum_{i=1}^m\left(X_i-X_i / I_i\right)^2}{m}} MRSE=m∑i=1m(Xi−X^i)2=m∑i=1m(Xi−Xi/Ii)2

| 模型 | R M S E RMSE RMSE |
|---|---|
| X t = ( 893.128 + 1.583 t ) S j X_t = (893.128 +1.583t)S_j Xt=(893.128+1.583t)Sj | 7.665 |
| ∇ 12 ∇ X t = ( 1 − 0.234 B ) × ( 1 − 0.704 B ) 12 ϵ t \nabla_{12} \nabla{X_t} =(1-0.234B)\times (1-0.704B)^{12}\epsilon_t ∇12∇Xt=(1−0.234B)×(1−0.704B)12ϵt | 3.215 |
| ∇ 12 ∇ X t = 1 − 0.670 B 12 1 + 0.234 B ϵ t \nabla_{12} \nabla{X_t} =\frac{1-0.670B^{12}}{1+0.234B}\epsilon_t ∇12∇Xt=1+0.234B1−0.670B12ϵt | 3.215 |
