当前位置：首页 > news >正文

实验设计如何拯救我的 CEI VSR 28G 设计

news 来源：原创 2025/6/6 18:19:03

为了确定总体设计裕量，CEI 28G VSR/100 Gb 以太网设计需要分析 500 万种通道变化、收发器工艺和均衡设置的组合。蛮力模拟需要 278 天，这显然超出了可用的时间表。

相反，我们使用实验设计（DOE）和响应面建模（RSM）将模拟次数减少了 19,000 倍，但产生了同样有意义的结果。

本文将演示 DOE 和 RSM 在 CEI 28G VSR 设计中的应用。我们将展示创建 DOE、将数据拟合到模型、确定拟合的优度和可靠性，然后使用模型执行“假设”分析、优化设计因素和量化制造变化的影响的过程。

介绍

CEI VSR 28G/100 Gb 以太网链路的单位间隔仅为 35.7 ps，是一项具有挑战性的系统级设计。在本文中，我们介绍了系统设计过程，该流程产生了业界第一个采用 Inphi 的 GearBox 和 CDR 芯片的 100 Gb 以太网 CMOS PHY。抖动预算紧张，并且由于系统中可能存在各种变化，因此有超过 500 万个系统条件需要检查和验证性能。此外，为了确保系统不会设计过度或性能不佳，需要估计制造变化对性能和制造良率的影响。同时实现和优化所有这些目标确实是一项严峻的挑战。

下一代核心路由器和数据中心需要更多的带宽、更快的速度和更低的功耗。这迫使该行业实施高达 28 Gbps 的线路速度。图 1 给出了此类接口的示例拓扑，显示了芯片到模块应用，其中可插拔光收发器 CFP2 模块连接到线卡主机 IC。不要被看似干净的通道所迷惑，这里有很多损伤，并且比特误差率（BER）容限仅为千万亿位中的一个误差，这是一个世界级的挑战。

1：28G VSR 主机到模块通道图。

CMOS 设计使 Inphi 能够将功率包络降低到竞争对手 SiGe 和 FPGA 解决方案的三分之一和一半的面积。

设计过程中的众多挑战之一是确保发射器和接收器能够在各种通道中运行，包括一些超过 28G VSR 10 dB 主机到模块通道的通道。这里使用实验设计（DOE）和响应面建模（RSM）来确定最大允许走线长度、PCB 布线的最佳层、最佳过孔反焊盘尺寸以及由于 IC 工艺、电压和温度（PVT）的制造差异而导致的性能下降;封装阻抗;印刷电路板（PCB）阻抗;以及 Via Stub Length 变化。将解决这些设计目标中的每一个，我们将说明 DOE/RSM 方法如何提供明智的路径来回答这些问题。

问题是，尽管系统配置的每个模拟只需 4.8 秒即可完成，但要检查 500 万个条件则需要 278 天的计算时间才能完成！大型计算场会有所帮助，但如果在探索空间中添加其他因素，或者如果模拟需要更多时间才能完成，则很容易被结果的计算和存储所淹没。使用的链路仿真方法是一种快速分析方法，用于估计链路配置的 1e-12 BER。如果使用逐位时域分析来估计性能，那么仿真时间很容易接近每个 5 分钟。在这种计算负载下，500 万个案例只需要 47.5 年的计算时间。在这种情况下，蛮力分析不会是一个非常有效的工具。我们需要找到另一种方式。

理想情况下，如果有一个神奇的方程式，考虑到走线长度、阻抗和工艺拐角等输入因素，可以准确揭示最终的系统性能，那就太好了。这个神奇的方程式将支持多种分析，如优化、虚拟“假设”分析，以及定位设计以最大限度地减少制造差异影响的能力。

当然，这并不完全可能，但通过将 DOE 与 RSM 结合使用，我们可以实现这一理想。DOE 用于对因子空间进行采样，RSM 用于创建最适合数据的方程（或模型）。在验证了模型的正确性之后，我们可以利用它来做上述所有事情，优化、执行“假设”分析，并最大限度地减少制造变化的影响。DOE/RSM 流程在下面的图 2 中可视化，这是为了强调分析的迭代性质。此外，分析的每个阶段都有一定的假设，在获得满意的结果之前，需要重新审视和修改这些假设。

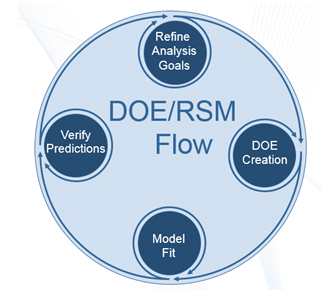
图 2：实验设计（DOE）和响应面建模（RSM）方法流程。

分析方法

任何类型分析中最重要的一步都是确定工作的目标。据称，阿尔伯特·爱因斯坦曾说过：“如果我只有一个小时来拯救世界，我会花 55 分钟思考问题，而只有 5 分钟思考解决方案”。同样，在开始使用 DOE/RSM 方法的实际工作之前，明确定义要解决的问题和答案的准确性水平是绝对必要的。明确的分析目标将使您处于实现目标的最佳位置。

DOE 和 RSM 流程图强调了分析的迭代性质，因为它允许在过程的每个步骤中完善假设。也可以看出，如果没有明确的分析目标和退出标准，这样的做法可能会导致周末的损失和永无止境的评论。

对于一些人来说，一种表示完整性的统计思维方式，即在存在不确定性的情况下做出决策，是令人不舒服的。DOE/RSM 分析将提供置信区间之间的答案，表明结果的准确性，而不是依赖于详尽的确定分析。详尽确定的思维方式和统计思维方式之间的唯一区别是，在前者中，任何不确定性都被假装消失了，而在后者中，不确定性被量化、仔细审查和传达。无论我们是否愿意，总会存在不确定性，最好的方法是理解它，减少它并接受它。适应不确定性。

请注意，JMP 统计发现软件用于 DOE 创建和模型拟合分析。本文档中的许多图都来自 JMP 报表或源自 JMP 报表。系统链路仿真是使用 SiSoft 的 Quantum Channel Designer （QCD）进行的。®®®

假设

除了思维方式的改变之外，DOE/RSM 技术还需要对所应用的相关统计概念有深入的了解，这可能是一个挑战。我们将在本文中使用的方法是首先讨论一些关键概念和其中的假设，然后提供 VSR 28G 接口设计方法的可靠应用示例。

一般来说，对对象进行建模就是利用对感兴趣方面的某个方面的简化描述，从而允许探索对象的特征。一个物理示例是在风洞中使用模型飞机来研究其空气动力学特性，以帮助设计全尺寸飞机。对我们来说，要建模的对象有点模糊，但通常是系统性能的响应，例如眼高或眼宽在研究因子范围内的响应。

建模目标是通过对因子空间（如 DOE 表提供）进行采样来描述真实响应的特征，然后将多项式方程拟合到数据。从这个意义上说，模型实际上是最适合数据的方程。这种模型的一个直观示例如下图 3 所示，其中给出了链路的眼高与走线长度和阻抗的关系。

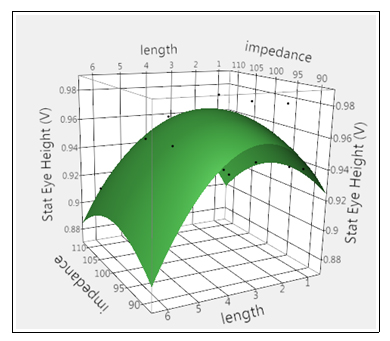
图 3：眼高响应面示例与走线长度和阻抗的关系。

请注意，该模型只是实际响应的近似值，并且仅在准确的情况下代表现实。此外，从表面的曲率可以看出，该模型是最适合数据的二维抛物线。模型形式和从普通最小二乘拟合中获得的系数估计值在下面的公式（1）中给出：

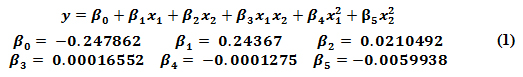
尽管这个表面代表了模型与数据的最佳拟合，但它并没有解决以下问题：这是表示“真实响应”的最佳模型吗？在这种情况下，为 length factor 添加更高的多项式项可能会更好地捕获 trace 的谐振行为。虽然找到绝对最佳模型可能是一个难以捉摸的目标，但我们当然可以通过逐步改进模型形式来实现它。“太简单”的模型会导致重要的响应特征被平滑化，而“太复杂”的模型会导致过分强调某些响应特征，而牺牲其他更重要的响应特征。

有人可能会认为，要找到最佳模型形式，只需将非常大范围的多项式项应用于模型拟合，以查看哪些项有效。这种方法的难点在于，可用于拟合的模型形式受响应采样的限制。如果沿因子维度只有两个数据样本，则最多可以有一条直线拟合到数据。如果有三个数据点，则最多可以拟合一条二次线，如果最多有四个数据点，则再拟合一条 3RD阶多项式可以拟合。因此，在某些时候，给定一个固定的采样集，可用于拟合的模型是有限的。这些限制导致这样一种观点：因子空间的抽样还必须考虑模型形式，以便模型拟合可以准确估计真实响应。

从概念上讲，使用连续因子可以迭代，直到获得理想的采样和模型形式，以实现高质量的模型拟合。但在实践中，互连的各个部分通常由可能只有离散数量的层级的块表示，例如以 S 参数模型为特征的连接器系列的情况。在这些情况下，采样的分辨率是固定的，而高阶系统响应特性与低阶系统响应特性混叠，从而限制了分析。

模型假设的最后一个方面是多项式可以充分描述响应曲面的想法。还有其他数学上更复杂的模型，例如高斯过程建模，它们具有一些令人惊讶的特性（例如零残差和空间认知插值），但在这里不讨论。作者发现，DOE/RSM 方法的绝大多数信号完整性应用都可以用多项式模型充分描述。

将模型拟合到数据的过程通常由普通最小二乘法（OLS）回归分析执行。此估计方法假定输入因子不相关，拟合误差方差不随因子或因子水平变化，并且残差呈正态分布。如果需要，可以放宽这些假设，但需要更复杂的最小二乘法，例如广义线性模型（允许除正态分布之外的其他残差误差分布）和一般最小二乘法（允许相关因子和非均匀误差方差）。在分析中，我们将对残差进行广泛的调查，以确保模型是适当的并且它满足 OLS 假设。

方法在 28G VSR 系统分析中的应用

该研究的全部目标是回答设计问题并量化 28G VSR 链路设计的制造差异。设计问题是，PCB 的哪一层更适合高速布线，最好的 PCB 过孔反焊盘尺寸是多少，以及在足够的系统性能下仍可以通过的最大 PCB 走线长度是多少？这些问题应该在存在制造差异的情况下得到回答，这也将被量化。

通过使用实验设计方法对因子空间进行仔细采样，评估这些 DOE 条件下的系统性能响应，将响应面模型拟合到数据以生成多维方程，然后可用于研究总因子空间。尽管此分析描述暗示了一个简单的进展，但在实践中它是相当迭代的，因为每个阶段的假设都经过改进，以获得具有足够准确性的令人满意的模型拟合。希望任何眼高和眼宽预测的不确定性小于 +/- 30 mV 和 +/- 0.5 ps。在第一次传递时达到所需的准确率很少发生（如果达到，那么它应该引起您的怀疑），但需要对模型假设、因子范围和 DOE 创建进行细微的修改。

下面的表 1 列出了定义要探索的领域的九个因素。直接影响设计决策的因素称为设计因素，生产中不可控的因素称为制造因素。

参数名称	因子类型	最小值	类型	麦克斯
Tx PVT 角	制造业	不锈钢	TT	FF 系列
Tx PKG	制造业	90 欧姆	100 欧姆	110 欧姆
线卡 PCB 过孔反焊盘尺寸	设计	32 密尔	36 密尔	40 密尔
线卡 PCB 过孔短线长度	制造业	2 密耳	10 密耳	18 密尔
线卡 PCB 布线层	设计	3	--	9
线卡长度	设计	1 英寸	3 英寸	6 英寸
线卡 TL 阻抗	制造业	90 欧姆	100 欧姆	110 欧姆
Rx PKG	制造业	90 欧姆	100 欧姆	110 欧姆
Rx PVT 角	制造业	不锈钢	TT	FF 系列

表 1：28G VSR 接口因子空间定义。

设计实验

传统上，有几种方法可以对大型多维因子空间进行采样。其中一些方法包括穷举抽样，其中评估每个条件;随机抽样，其中许多条件是偶然选择的;以及一次抽样一个因子，其中从名义条件中，每个因子都被孤立地扫描。任何类型抽样的目标都是获得总因子空间的表示，以便通过使用样本的统计数据来推断总因子空间。穷举抽样方法很好，但很可能是一种不切实际的方法。随机抽样方法（也称为蒙特卡洛抽样）可能是无偏的，但不能保证覆盖整个空间，并且需要许多采样点来确保考虑因子空间的所有区域。最后，一次抽样一个因子（有时称为 OFAT）会错过许多重要的因子交互作用。

试验抽样设计方法尝试对空间进行抽样，以提供整个因子空间的良好覆盖，同时最大限度地减少游程数。这是通过从随机采样开始，然后修改每个采样点，直到 DOE 集的覆盖范围足够来实现的。采样的覆盖率由样本预测方差量化，这可以通过一些简单的矩阵作轻松计算。预测方差的这种量化允许量化抽样的不确定性，从而优化采样。这就是为什么有些人称 DOE 方法为最佳设计。

对于我们的 VSR 示例，使用 256 次游程对 9 个因子进行抽样，并使用 D 最优方法使样本的预测方差最小。D 最优设计对因子空间的边的采样比对中心更多的采样，并且比其他最优性标准更准确地给出了模型参数估计。由于目标之一是找到因子空间的最坏情况（这些条件通常发生在空间的边缘），因此准确估计因子空间的边缘和角落非常重要。采样的假设模型为 2ND1 的 order 多项式圣对所有因子之间的交互进行排序。

运行模拟并处理模型拟合后，模型拟合预测的准确性将通过置信区间进行量化。较小的置信区间将比较大的置信区间提供更多的保证。置信区间大小取决于三个因素：所需的置信水平（95%、99%、99.9% 等）、模型拟合误差和 DOE 采样的覆盖率。在分析的 DOE 创建步骤中，了解 DOE 采样的覆盖率可以深入了解相对置信区间大小，并体现在预测方差中。虽然可视化 9 维空间是一项壮举，但我们可以用设计空间图的一小部分来总结整个空间的预测方差，如下图 4 所示。

图 4：设计空间分数图，显示空间分数上的 DOE 预测方差。

此图显示 50% 的因子空间的相对预测方差小于 0.19。虽然该指标的相对性质并不适合作为绝对的指导方针，但它允许对竞争设计进行比较。因此，建议生成一些设计，然后进行比较以选择最佳设计。

理想的设计（有时称为正交设计）是指能够独立计算参数估计值的设计。这仅适用于选定的设计，并且在大多数情况下（考虑到游程数和模型形式）无法进行正交设计。不过，设计可能接近正交特性。当设计不是正交的时，两个或多个参数效应彼此之间会略微相关，并且在一定程度上无法区分。在下面图 5 中的相关图上的彩图中，我们模型的所有 54 项的相关程度都可以量化。每个模型项的名称都为图的每一列给出，并且每个相应的行的名称相同。图中的颜色范围从蓝色（不相关）变为红色（完全相关）。图的红色对角线表示每个模型项都与自身完全相关，正如预期的那样，但最重要的是，没有红色的非对角线项，这表明设计不佳。

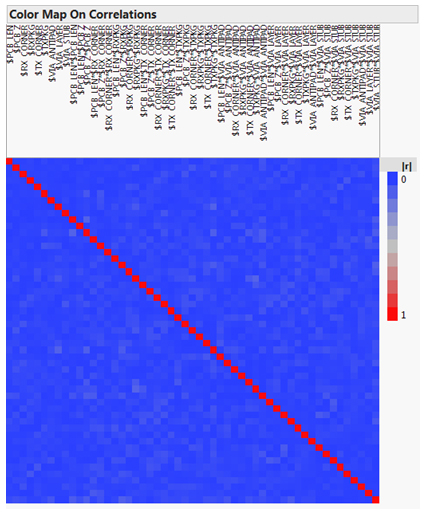
图 5：响应曲面设计中所有项的相关图上的色图。理想情况下，两个非对角线项之间的相关性为零，用蓝色表示。

为了将即将到来的模型拟合置于最佳位置，实验抽样设计找到了一个样本集，该样本集充分覆盖了因子空间，并允许对参数效应进行几乎独立的估计。

评估系统响应

将 DOE 采样条件引入 28G VSR 拓扑的 EDA 链路仿真环境中，进行仿真并计算链路性能指标。这里将考虑的指标是 BER 为 1e-12 时的眼高和眼宽。必须检查仿真结果波形的一致性和准确性。建议检查性能中的异常值，以确保它们体现真实的结果。在模型拟合期间，将假定每个条件都代表实际响应，因此任何差异都会将误差传播到模型拟合中，并导致分析结论不佳甚至错误。下面的图 6 是如何在 SiSoft 的 Quantum Channel Designer ® （QCD）中可视化结果的示例。

图 6：在进行模型拟合之前，必须仔细评估仿真结果，以确保所有结果都是合理的。

响应曲面模型拟合

到目前为止，已采取的所有预防措施都已完成，以获得良好的模型拟合。一旦拟合完成并测量了其质量，将确定这些预防措施是否足够，或者是否需要更多的迭代和改进。我们将使用的模型形式称为响应面模型，是一个具有交互项的多维多项式，如下面的方程（2）所示。这是测得的响应（例如眼睛高度）是 n=9 个因子之一，而是未知模型系数，将通过最小二乘法估计。

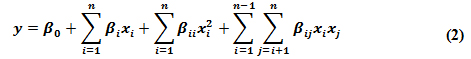
模拟的眼高与响应方程预测的眼高之间的差值称为误差残差。通过检查残差，我们可以获得模型质量的几个度量并验证假设。

拟合优度

最简单的拟合度量称为多重决定系数，但大家简称为“R 平方”，写成 R2.此指标的范围从 0 表示拟合差到 1 表示拟合良好。从概念上讲，100*R2可以看作是模型中可以解释的数据变异的百分比。一个有趣的事实是 R2如果添加其他模型术语，则无论这些新术语是否实际重要，指标都将始终提高。修改后的 R2metric 调用的R2调整，会考虑模型中使用的项数，并对任何额外的不必要项进行惩罚。因此，R2和 R2adjusted 表示模型中存在不必要的项。

拟合的误差标准差可以通过以下方法估计：取数据集中每个点的残差，对其进行平方，找到平均值，然后取平方根。此 RMSE 指标还可用作预测置信区间的快速估计值。对于 95% 置信区间估计值，只需将 RMSE 乘以 2 即可。如果 +/- 此值大于所需的精度，则有必要返回并重新访问之前的假设，例如在 DOE 创建中使用的模型形式和因子空间定义。

7：眼高（左）和眼宽（右）的拟合优度摘要。

如上图 7 所示，是眼高和眼宽拟合的 JMP 统计软件拟合汇总。我们看到 R2和 R2调整后的值为 90 年代，眼高的 RMSE 为 22 mV，眼宽为 0.45 ps。

最后，需要检查拟合误差残差本身，以确保它是正态分布的并且不包含任何“结构”。下面的图 8 显示了眼高度和宽度的残差分布，可以看作是大致呈正态分布的。

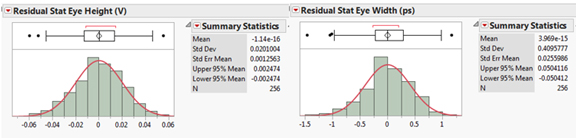
图 8：眼高（左）和眼宽（右）的拟合误差残差。这些表明残差大致按要求呈正态分布。

残差与响应或其他重要因子的图是在残差中搜索 “structure” 的最佳方式。结构，即残差和一些解释变量之间的一些系统关系，是模型偏差的证据，可以提供关于模型拟合中应包含哪些新项的线索。通常，由于 DOE 的采样不足，此类附加模型项无法立即使用，并且需要重新表述 DOE 创建，以便可以添加额外的模型项而不会使其他重要影响混叠。图 9 的下方是残差与响应的图。无论如何观察，残差都应该呈正态分布，但从图中可以看出，预测的最低眼高情况具有正残差，如图中圈出的那样。进一步的研究表明，额外的模型项 PCB_LEN*PCB_Z*RX_CORNER 改善了拟合度。尽管可能有更多这样的模型项可以提高拟合度，但准确性足以满足研究的需要，并且模型拟合被认为足够好。

图 9：残差与预测的眼高（左）和预测的眼宽（右）。残差中的系统结构表明模型偏差。请注意，最低眼高性能情况都具有正残差，这一观察结果导致包含一个额外的模型项，从而提高了拟合度。

虽然这些是非常好的模型拟合结果，但考虑剩余不确定性的来源还是很有趣的。残差只能来自两个来源，随机误差和失拟。对于确定性信号完整性仿真，没有随机噪声，因此残差完全是由于缺乏拟合造成的。在实践中，之所以无法实现完美的模型拟合，是因为潜在现象不是完美的多项式，还因为真正的潜在现象因子是乱码，仅由研究因子不完美地表示。

探索和优化 28G VSR 系统

一旦完成了所有作以确保正确拟合，我们就可以探索模型所表示的因子空间，并确信不确定性已大致理解。在此应用程序中，可视化 10 维空间是一项艰巨的任务，幸运的是，有一些工具可以促进这种类型的分析。一个称为预测刻画器的图显示如果所有其他因子都保持不变，每个因子的响应将是什么。这种类型的绘图在交互使用时最有用，但也可以从下面使用的静态视图中收集到很多信息。例如，考虑两个因子 RSM 拟合的预测刻画器图，如图 10 所示。

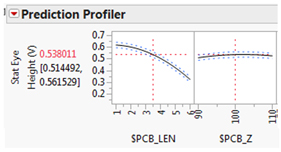
图 10：预测眼高响应的预测刻画器示例图。它显示了在所有其他因子保持不变的情况下，相对于每个因子的响应。

此预测刻画器图显示了跨解释因子、走线长度（PCB_LEN）和走线阻抗（PCB_Z）的眼高响应。由于迹线长度因子的斜率最大，我们可以说这是因子空间的这个区域中影响最大的因子。如果因子之间存在任何交互作用，则线的有效斜率可能会在因子空间的其他区域中发生变化。此外，该图表明，当 PCB_LEN=3.5 且 PCB_Z = 100 时，预测的眼高为 0.538 V，95% 置信区间为 [0.514， 0.562] V，这相当于表示预测的眼高为 0.538 +/- 0.0234 V，置信区间为 95%。置信区间在预测刻画器图中由黑色实线预测响应周围的蓝色虚线表示。

置信区间（有时缩写为 CI）可以被认为传达以下信息：

置信区间为真实响应提供一系列合理值，超出该范围的值相对不可信，或者
CI 给出估计的精度，其中上限和下限提供可能的最大估计误差，尽管可能存在更大的误差。

95% 的置信水平大致涵盖与预测值的 2 个标准差，而 99.5% 的置信水平大致涵盖与预测值的 3 个标准差。图 11 给出了示例因子空间中间的预测刻画器图。

图 11：眼高（顶行）和眼宽（底行）因子空间中间的预测刻画器。重要因素可以通过曲线的斜率来识别

如前所述，走线长度是该空间区域中影响最大的因素。这两行图分别用于眼睛高度和眼睛宽度。如果希望了解某个因子对空间的这个区域的影响，此图很容易提供此信息。

由于拟合的响应表面由定义明确的函数表示，因此可以在空间中搜索最坏情况，如图 12 中的预测刻画器图所示。

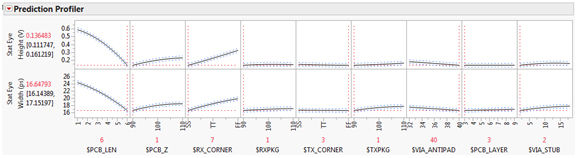
图 12：在预测的最坏情况下，眼睛高度（顶行）和眼睛宽度（底行）的预测剖面图。

需要注意的是，虽然走线长度仍然是空间这个区域最有影响力的因素，但与它们在因子空间中间的影响相比，走线阻抗和接收器 PVT 拐角（$RX_CORNER）也变得有些影响。

确定高速信号的 routing 层

这里使用的设计优化策略是首先确定最坏情况的制造条件，然后将设计因素置于最佳情况条件下，以最大限度地减少最坏情况性能的影响。

为了量化 PCB 布线层在最坏情况拐角处的影响，计算了 PCB_LAYER=3 和 PCB_LAYER=9 的预测响应并进行比较。如下图 13 所示（请注意，纵轴已缩放以提供更好的视图），两个 PCB 层之间的眼高和眼宽差仅为 0.012 mV 和 0.35 ps。另请注意，眼高的 95% 置信区间为 +/-24 mV，眼宽的 95% 置信区间为 +/- 0.5 ps。当预测的差异小于置信区间时，可以说模型无法自信地将效应识别为显著，并且没有提供任何可作的信息。这可能会得出以下结论：

PCB routing 层是系统性能的弱预测器，第 3 层和第 9 层是等效的，或者
PCB routing layer 9 与 layer 3 相比具有轻微但不显著的优势。

如果这些结论中的任何一个都不足，那么将需要有关这两个层的影响的额外信息来做出明确的决定。可以围绕该因子定义一个更集中的 DOE/RSM，其中从研究中删除了一些其他不重要的因子，以提高分析的准确性。此外，在做出任何决策时，应考虑对 routing layer 决策的其他影响，例如 PCB 空间成本或金钱成本。

对于 VSR 研究，将得出结论， PCB 布线层 9 比第 3 层略有优势（尽管在统计上不显著）。

图 13：如何评估整个 PCB 层因子的“假设”场景的示例。左侧的曲线显示了 PCB 布线层位于第 3 层时的预测响应，右侧的曲线显示了当 PCB 布线层位于第 9 层时的预测响应。

确定最佳过孔反焊盘尺寸

将采用类似的方法来了解 PCB 对反焊盘尺寸的影响。对于眼高，32 和 40 mil 的反焊盘直径之间的链路性能差异为 45 mV 和 0.47 ps，其中眼高置信区间为 +/- 25 mV，眼宽置信区间为 +/- 0.5 ps，置信度为 95%。从图 14 中的预测刻画器图中可以直观地看出这一点，因为眼高图的红色水平虚线不包含在蓝色虚线置信区间线中，而红色虚线包含在眼宽的蓝色置信区间虚线中。因此，我们可以得出结论，32 mils 的反焊盘尺寸是眼高的更好解决方案，并且可能是眼宽性能的更好解决方案，但在统计上无关紧要。在做出最终决定之前，应仔细权衡其他限制，例如制造给定的防焊盘直径时增加的制造问题。

对于这项研究，未来的分析将使用 32 mils 的反焊盘尺寸。

图 14：跨过孔反焊盘因子的“假设”分析，显示了不同过孔反焊盘尺寸之间的性能差异。

需要澄清的一点是，虽然 DOE/RSM 方法可以量化给定因素的影响，但它无法说明原因。在给定情况下，某个因素有影响的原因必须来自主题专业知识和工程判断。如果没有令人满意的物理解释，那么重要性的统计指示可能是进一步分析的动力，并且对数据的竞争性物理解释做出假设可能很有用。

制造变化

量化制造变异的一种方法是为每个因子分配概率分布函数 （PDF），然后随机生成数百万个案例。利用响应面方程，可以量化每个随机情况的系统性能，并用于指示产生特定系统性能水平的概率。必须非常小心才能获得准确的 PDF，因为尾部的权重会在此类分析中产生很大差异。图 15 显示了预测刻画器图和分配给每个制造因子的 PDF。

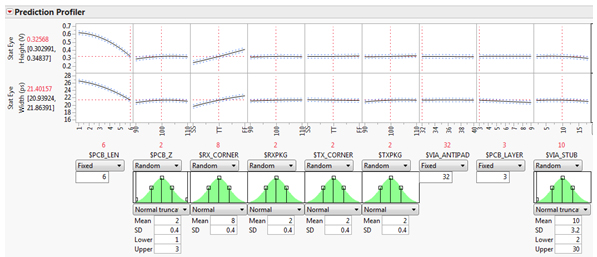
图 15：预测刻画器图，其中分配了分配给每个制造因子的分布。根据这些分布对因子空间进行随机抽样将提供制造 Yield 信息。

希望将制造变化理解为线卡走线长度的函数。因此，对于 1 、 2 、 3 、 4 、 5 和 6 英寸的线卡长度，随机生成 100 万个案例，并使用响应面方程计算眼高和眼宽性能。图 16 中给出了每种长度的 100 万个案例的平均值和标准差。该分析清楚地表明，对于眼高，制造变化的影响随着线卡走线长度的增加而增加。增加的一个可能解释不是当线卡走线长度等于 6 英寸时会发生更多的制造变化，而是系统更容易受到上述变化的影响。还应注意的是，眼宽变化随轨迹长度的增加而变化非常小。图 16：制造良率预测与最大允许的迹线长度。竖条表示每个产量分析的标准差，并显示眼高变异性随着痕量长度的增加而增加。

每百万缺陷数分析

最后一项分析是对每百万个缺陷数的估计。如果因子 PDF 和响应面方程是准确的，则可以计算系统的制造良率。此分析的通过/失败标准取决于模拟中包含的链接不确定性以及预算中的链接不确定性。在本例中，通过系统的规格限值为 200 mV 的眼高和 19 ps 的眼宽。对于线卡长度为 6 英寸的系统，眼高和眼宽的产量分布图如下图 17 所示。

图 17：每百万缺陷数（DPM）分析，根据眼高和眼宽要求分别显示预测的 225 和 170 DPM。

此处，规格下限（LSL）绘制在分布上，显示了低于此限值的分布百分比以及相应的百万分之几（PPM）值 224 和 170 个/百万缺陷。

结论

我们已经展示了有助于第一个 CMOS 28G VSR / 100G 以太网 PHY 设计的方法。接口设计问题：要布线的 PCB 层、使用多大尺寸的过孔反焊盘以及允许的最大走线长度。确定了最坏的情况，并量化了制造变化对性能的影响。所有这些都是通过 DOE/RSM 方法完成的。DOE 无需数月的计算时间来模拟数百万种情况，而是仅用 256 次运行就对因子空间进行了智能采样。最小二乘模型拟合找到与数据最拟合的响应曲面，在验证模型后，它用于预测整个因子空间的系统性能。必须强调的是，随着模型假设的变化，需要对方法进行多次迭代。总体而言，DOE/RSM 方法已被证明是理解和优化令人眼花缭乱的大因子空间的强大方法，并为 Inphi 的成功做出了贡献，推出了世界上第一个生产就绪的 100G CMOS PHY/SerDes 变速箱。