基于VMD-LSTM融合方法的F10.7指数预报
F10.7 Daily Forecast Using LSTM Combined With VMD Method

F10.7 solar radiation flux is a well-known parameter that is closely linked to solar activity, serving as a key index for measuring the level of solar activity. In this study, the Variational Mode Decomposition (VMD) and Long Short-term Memory (LSTM) network are combined to construct a VMD-LSTM model for predicting F10.7 values. The F10.7 sequence is decomposed into several intrinsic mode functions (IMF) by VMD, then the LSTM neural network is utilized to forecast each IMF. All IMF prediction results are aggregated to obtain the final F10.7 value. The data sets from 1957 to 2008 are used for training and the data sets from 2009 to 2019 are used for testing. The results show that the VMD-LSTM model achieves an annual average root mean square error of only 4.47 sfu and an annual average correlation coefficient (R) of 0.99 during solar cycle 24, which is significantly better than the accuracy of the LSTM model (W. Zhang et al., 2022), the AR model (Du, 2020), and the BP model (Xiao et al., 2017). The VMD-LSTM model exhibits strong predictive capability for the F10.7 index during solar cycle 24.
F10.7 太阳辐射通量是一个众所周知的参数,与太阳活动密切相关,是衡量太阳活动水平的关键指标。在本研究中,变分模态分解 (VMD) 和 长短期记忆 (LSTM) 网络被结合起来,构建了一个 VMD-LSTM 模型 用于预测 F10.7 值。F10.7 序列首先通过 VMD 分解为多个本征模态函数 (IMF),然后利用 LSTM 神经网络对每个 IMF 进行预测。将所有 IMF 的预测结果聚合,即可得到最终的 F10.7 预测值。1957 年至 2008 年的数据集用于训练,2009 年至 2019 年的数据集用于测试。结果表明,在太阳活动第 24 周期间,VMD-LSTM 模型的年平均均方根误差 (RMSE) 仅为 4.47 sfu,年平均相关系数 (R) 达到 0.99。该精度显著优于 LSTM 模型 (W. Zhang et al., 2022)、AR 模型 (Du, 2020) 和 BP 模型 (Xiao et al., 2017) 的精度。VMD-LSTM 模型在太阳活动第 24 周期间对 F10.7 指数表现出强大的预测能力。
Key Points
The Variational Mode Decomposition (VMD) algorithm can effectively address nonlinear problems of F10.7 sequence
The VMD algorithm can significantly improve the prediction accuracy of single Long Short-term Memory (LSTM) model
In solar cycle 24, the VMD-LSTM model has stronger predictive capability than other classical models
1 Introduction
F10.7 指数(也称为渥太华指数或科温顿指数)测量的是波长为 10.7 厘米(频率为 2800 MHz)的太阳辐射通量。它被认为是表征太阳活动水平的最佳指标之一,反映了日冕上所有源区的总射电辐射通量值,其单位为太阳通量单位(sfu)(1 sfu = 10⁻²² W·m⁻²·Hz⁻¹)。在大多数情况下,F10.7 指数的值范围在 50 到 300 之间 (Svalgaard, 2016)。
F10.7 指数在确定和预测空间天气方面具有非常重要的价值。它已广泛应用于众多高层大气模型(例如,Hedin, 1988; Picone et al., 2002)和电离层模型(例如,Adebiyi et al., 2016; Benoit & Petry, 2021)中。其长期数据记录为六个太阳周期提供了气候信息。此外,由于 F10.7 可以在任何天气条件下从地面进行准确可靠的测量,因此它是一个非常可靠的数据集,几乎没有数据缺失或校准问题。
目前,许多研究采用了不同的方法来预测 F10.7 指数。Henney 等人 (2012) 利用通量输运模型生成的全球太阳磁场来预测 F10.7 指数,提前一天的预测斯皮尔曼相关系数达到 0.97。Liu 等人 (2018) 结合了两个太阳表面通量输运模型(Worden & Harvey, 2000; Yeates et al., 2007)来估算太阳磁场并预测 F10.7 指数,其提前 3 天预测的斯皮尔曼相关系数高于 0.95。Lei 等人 (2019) 基于太阳极紫外图像中 F10.7 观测值与 PSR(该指数由太阳 EUV 图像的强度值定义)之间的关系建立了一个经验预测模型。与 2012 年至 2013 年期间 54 阶自回归模型的预测结果相比,该经验模型的误差降低了 12.54%。
随着机器学习和人工智能的发展,各种机器学习技术已被用于预测 F10.7 指数的非线性和周期性变化模式。例如,Chatterjee (2001) 使用多层前馈神经网络,以过去 11 天的历史值作为模型输入,提前一天预测 F10.7 指数,获得了约 0.93 的相关系数。C. Huang 等人 (2009) 应用支持向量回归(Support Vector Regression) 预测了 2002 年至 2006 年的 F10.7 指数值,其平均绝对百分比误差在 2.71% 到 5.56% 之间。Warren 等人 (2017) 提出了一种 F10.7 的线性预测模型。Wang 等人 (2018) 建立了一个结合相关性和不同滞后项(注:原文 "different parties" 结合上下文应为 "different lags" 或类似含义)的线性多步预测模型,以增强 F10.7 指数的多步预测性能。这些机器学习模型可以在特定情况下解决一些问题,但它们中的大多数通常只在浅层进行训练,无法充分提取数据中的隐藏信息,尤其是复杂的时间周期性变化。
然而,深度学习方法能够通过深入且广泛的训练来充分优化损失函数,从而学习时间数据的周期性变化 (Kingma & Ba, 2014)。 Xiao 等人 (2017) 采用反向传播神经网络 (Back Propagation Neural Network) 预测 F10.7 指数,与其他模型相比,该模型表现出更好的短期预测精度。Luo 等人 (2022) 将卷积神经网络 (Convolutional Neural Networks) 与长短期记忆网络 (LSTM) 相结合,预测了 2003 年至 2014 年期间未来 27 天的 F10.7 值。Gao 等人 (2022) 将太阳黑子数整合到 LSTM 中,基于 54 天的太阳辐射通量指数,建立了一种预测未来 7 天 F10.7 的短期预测方法,其均方根误差 (RMSE) 比美国空间天气预报中心 (SWPC) 的模型低 11%。W. Zhang 等人 (2022) 使用 LSTM 模型对 F10.7 指数进行短期预测,并验证了 LSTM 模型优于普通神经网络模型。
与此同时,VMD 算法已在许多工作中得到广泛应用。 Niu 等人 (2018) 建立了 VMD-ARIMA-HGWO-SVR 模型以提高集装箱吞吐量预测的稳定性和准确性。误差分析和模型比较结果表明,VMD 比 CEEMD 和 WD 等其他分解方法更有效。Abdoos (2016) 将 VMD 与极限学习机 (Extreme Learning Machines) 结合用于短期风速预测,与先前报道的方法相比,该方法在精确预测和节省计算时间方面具有优势。Y. Zhang 等人 (2019) 提出了一种基于 VMD-小波变换 (VMD-WT) 和主成分分析-反向传播筛选-径向基函数神经网络 (PCA-BP-RBF) 的混合模型用于短期风速预测。实验结果表明,VMD-WT 能更好地解决模态混叠和端点效应问题,使得本征模态函数 (IMF) 的周期性特征更加明显,从而提高了预测性能。
目前,F10.7 指数的预测模型具有良好的预测性能。然而,以往的模型很少考虑预测序列本身的非线性问题,预测精度仍有提升空间。 为了提高 F10.7 指数的预测精度,本研究引入 VMD 算法对 F10.7 指数进行分解以重构预测。VMD 算法能有效解决时间序列数据的周期性和强非线性问题。 同时,LSTM 神经网络在低复杂度和低非线性的时间序列上表现出良好的预测能力。 因此,将 VMD 方法与 LSTM 模型相结合,构建了一个用于 F10.7 指数的 VMD-LSTM 预测模型,以期进一步提高 F10.7 指数的预测精度。
2. Method
2.1 VMD (Variational Mode Decomposition)
变分模态分解 (VMD) 方法最初由 Dragomiretskiy 和 Zosso (2014) 提出。它能够平滑非平稳信号并将其分解以获得不同本征模态函数 (IMF) 的分量。使用这种方法,可以将非平稳和非线性信号分解成具有不同时间尺度的平稳信号。初始的 IMF 分量代表原始信号的高频部分。随着分解层级的增加,对应的 IMF 频率变小,周期变大 (Sain & Stephan, 1997)。
与经验模态分解算法 (EMD) (N. Huang et al., 1998) 的递归分解模式不同,VMD 算法将信号分解转化为变分分解模式。通过多个自适应 Wiener 滤波器组,分解出的分量可以被自适应地分割。这非常有效地克服了分解中出现的模式混淆现象,即同一分量出现在不同频带,或不同分量出现在同一频带。
VMD 的具体实现步骤如下:
- 对信号进行 Hilbert 变换后,分析得到的解析信号,并计算其单边频谱。
- 然后将其乘以中心带调制,将其移至相应的基带。
- 计算解调信号梯度的范数,并估计每个模态的信号带宽。
- 约束变分问题表述如下:

为了将约束变分问题转化为无约束变分问题,引入一个拉格朗日乘子算子 λ 和一个二次惩罚因子 α。在存在高斯噪声的情况下,α 确保信号重建的准确性并保持约束的严格性,以获得约束变分问题的最优解。表达式如下:
其中:
-
u_k代表每个模态函数, -
ω_k是每个模态的中心频率, k = 1, 2, …, N。-
λ是拉格朗日乘子, -
δ是 Dirac 分布(狄拉克函数), -
f(t)是解析信号。
然后,使用乘法算子交替方向法 (multiplicative alternating direction algorithm) 来解决上述问题,并不断更新分量及其中心频率以获得最优解。
总的来说,VMD 是一种将待分解信号转换为非递归和变分模式的分解方法,能够很好地分解噪声信号。VMD 的整体框架是一个变分问题。它假设每个模态具有有限带宽且具有不同的中心频率。在噪声信号被分解后,通过使用乘法算子的交替方向法不断更新每个模态及其对应的中心频率,即可获得每个变分模态分量及其中心频率。
2.2 GA (Genetic Algorithm)
在信号处理中使用变分模态分解(VMD)时,分解结果显著受分解模态数(K)和惩罚参数(α)的影响。如果K值过高,可能会产生虚假分量;而如果K值过小,则可能丢失相关分量。另一方面,α值影响分解后的本征模态函数(IMF)的带宽——较高的α值导致较窄的带宽,而较低的α值导致较宽的带宽。因此,优化参数K和α至关重要。
为了确定VMD中的最优参数K和α,本研究选择了一种名为遗传算法(GA)的流行方法进行VMD参数优化。与其他优化算法(如蚁群算法和粒子群算法)相比,GA因其普适性、搜索效率和强大的全局优化能力而被选用(Chen et al., 2023)。GA是一种基于自然选择和遗传原理的非线性全局优化算法。使用GA优化VMD参数的过程涉及六个主要步骤:编码、种群初始化、适应度评估、选择、交叉和变异。其中,适应度评估步骤尤为关键,它指导优化过程,需要定义一个合适的适应度函数来评估个体接近最优值的程度。
在本研究中,采用GA优化VMD的模态数K和惩罚因子α。选择的适应度函数是包络熵(Ep),它表征了原始信号的稀疏特性。包络熵值越高,表明IMF中噪声越多,特征信息越少;反之亦然。信号x(i) (i = 1,2, …, N)的包络熵(Ep)可以用公式(9)表示。公式中的a(i)是通过对VMD分解的第k个模态分量进行希尔伯特(Hilbert)解调得到的包络信号,ε(i)是通过计算a(i)的归一化得到的概率分布序列,N是采样点数。概率分布序列ε(i)的熵值即为包络熵Ep。

在GA优化的VMD背景下,参数设置定义如下:K的范围为[2, 10],α的范围为[0, 5000],迭代次数设为50,种群大小为30,交叉概率为0.9,变异概率为0.1。本文首先使用1957年至2008年的训练数据优化VMD的超参数,然后将此优化过程获得的最佳VMD超参数应用于分解1957年至2008年的训练数据和2009年至2019年的测试数据。这样做是为了确保模型仅基于训练集内的信息构建,并计算了个体对应的包络熵。使用适当的收敛因子进行迭代更新,直到满足终止条件,从而确定最优的VMD参数。
2.3 VMD-LSTM
作为增强型循环神经网络,LSTM 网络不仅能有效解决传统 RNN 面临的长距离依赖问题,还能解决神经网络中常见的梯度爆炸或消失问题(Graves, 2012; Tan et al., 2018)。它在处理序列数据方面非常有效。它可以通过分解来降低序列的非线性和复杂性。因此,本文将 LSTM 神经网络模型与 VMD 算法相结合,以提前一天预测 F10.7 指数。这种组合方法被称为 VMD-LSTM 模型。
1. 分别应用 VMD 算法分解了 1957 年至 2008 年的训练数据和 2009 年至 2019 年的测试数据,得到了三个分量和一个残差。
2. 这些分解后的分量使用一个具有两个隐藏层、每层 50 个神经元的堆叠式 LSTM 模型进行独立训练。在完成 LSTM 模型的训练后,可以获得每个分量的预测结果。
3. 最后,通过将每个分量提前一天的预测结果累加起来,就能得到提前一天的 F10.7 预测值。
Figure 3
Prediction process of combined Variational Mode Decomposition algorithm-Long Short Term Memory neural network model for F10.7 index.
VMD-LSTM 是一个滚动预测模型,其时间步长为 7 天。这意味着提前 1 天的 F10.7 值是通过前 7 天的历史值来预测的。数据采用最小-最大归一化 (Min-Max Normalization) 方法进行处理。该方法将数据缩放到一个指定的范围内,通常为 0 到 1 之间。最小-最大归一化的公式为:

此处,X 是 F10.7 数据,Xnormalized 是归一化后的值,Xmin 是数据集中的最小值,Xmax 是数据集中的最大值。
预测模型由一个双层 LSTM 网络构成。它使用 Adam 优化器,批大小 (batch size) 设置为 32。同时,学习率 (learning rate) 设置为 0.001,训练轮数 (epochs) 设置为 100。
在本研究中,选择了两个评估指标来衡量模型的性能,即相关系数 (R) 和 均方根误差 (RMSE)。

![]()
其中,N 是样本数量,Xi 是预测值,Yi 是观测值,Xˉ 是 Xi 的平均值,Yˉ 是 Yi 的平均值。
- R 代表观测值与预测值之间的相关性。该值越接近 1,表示预测值与观测值匹配得越好。
- RMSE 反映了预测值与观测值之间的偏差。该值越小,表示预测模型越好。
3 Results
3.1 Analysis of Decomposition Results
GA-VMD 方法要求首先使用遗传算法 (GA) 找到与信号对应的最优参数组合。 优化过程中适应度随迭代次数的变化如图 4 所示。如图 4 所示,最佳适应度在第 25 次迭代时达到。通过算法的搜索过程,找到了最优参数组合 (K, α) = (3, 2626)。在确定了最优参数组合后,根据最优参数使用 VMD 对信号进行分解,以达到最佳分解效果。图 5 展示了 VMD 分解后得到的本征模态函数 (IMF) 分量,按从低频到高频排列。
Figure 4
Genetic algorithm for Variational Mode Decomposition parameter optimization results.
Figure 5
Decomposition results of the Variational Mode Decomposition method for the F10.7 index.
对于 VMD 后得到的序列,利用样本熵 (Sample Entropy) 来评估序列的复杂度,并利用总谐波失真 (Total Harmonic Distortion, THD) 来评估其非线性程度。失真的程度取决于非线性水平 (N. Huang et al., 1998)。样本熵由 Richman 和 Moorman (2000) 提出,是分析非平稳时间序列的综合指标。其核心原理涉及量化序列内生成新子序列的可能性。时间序列的复杂度通过评估信号内产生新模式的概率来衡量,产生新模式的概率越高,表明序列的复杂度越高。谐波失真是指当音频信号被放大时,由于系统并非完全线性,输出信号中出现了输入信号中不存在的额外谐波分量。本文通过计算新增加的总谐波分量的均方根值占原始信号均方根值的百分比来量化 THD。
表 1 给出了 F10.7 数据集的样本熵和 THD 结果。从表 1 可以观察到,F10.7 原始信号的样本熵 (2.33) 高于其 IMF 分量的样本熵。这表明原始信号相对更复杂。IMF1、IMF2 和 IMF3 的样本熵依次增加,残差 (RES) 的样本熵为 1.50。同时,IMF3 的 THD 最低 (1.09),其次是 IMF2 (2.87)、RES (6.97) 和 IMF1 (28.34),而 F10.7 原始信号的 THD 最高 (28.37)。THD 值越高,表明信号内非线性因素的影响越显著。总体而言,F10.7 信号显示出较高的样本熵,表明其复杂度较高且可能存在新的模式。另一方面,高 THD 表明信号内存在显著的非线性影响,尤其是在 F10.7 原始信号和 IMF1 分量中。
Table 1. Gives the Sample Entropy and Total Harmonic Distortion Obtained for the F10.7 Data Set
| F10.7 | IMF1 | IMF2 | IMF3 | RES | |
|---|---|---|---|---|---|
| Sample Entropy | 2.33 | 0.52 | 0.84 | 0.95 | 1.50 |
| THD | 28.37 | 28.34 | 2.87 | 1.09 | 6.97 |
3.2 Prediction Results
本研究评估了 LSTM 和 VMD-LSTM 模型在太阳活动低年和高年预测 F10.7 指数方面的性能。 选取 2009 年和 2014 年进行分析。结果表明,VMD-LSTM 模型在 RMSE 和 R 值方面均优于 LSTM 模型。对于 2009 年,LSTM 模型的 RMSE 和 R 值分别为 1.13 sfu 和 0.93,而 VMD-LSTM 模型的 RMSE 和 R 值分别为 0.89 sfu 和 0.95。同样,对于 2014 年,LSTM 模型的 RMSE 和 R 值分别为 9.89 sfu 和 0.94,而 VMD-LSTM 模型的 RMSE 和 R 值分别为 8.20 sfu 和 0.95。图 6 和图 7 显示,VMD-LSTM 模型的预测偏差低于 LSTM 模型,并且与观测值相对一致。然而,随着太阳活动增强,两种模型的预测值之间的偏差也会增大。在大多数情况下,VMD-LSTM 模型的预测偏差低于 LSTM 模型。总之,VMD-LSTM 模型的预测值比 LSTM 模型更接近观测值。LSTM 模型通常以端到端的方式进行训练,将时间序列的所有信息映射到一个向量中。该向量整合了不同维度的信息,使其容易过拟合并对序列中的噪声更敏感。经过 VMD 分解后,F10..7 序列被分解为多个子序列。与原始序列相比,每个子序列包含的不同维度信息更少,从而降低了序列的非线性和复杂性。同时,这种分解方法有效解决了 EMD 方法中常见的端点效应和模态分量混叠等问题。因此,VMD-LSTM 模型能够取得更好的预测结果。
Figure 6
The comparison of the Variational Mode Decomposition algorithm-Long Short Term Memory neural network prediction values with the observations in 2009 and 2014.
Figure 7
The difference obtained by subtracting the predicted values of Variational Mode Decomposition algorithm-Long Short Term Memory neural network (LSTM) from the observed values, and the difference obtained by subtracting the predicted values of LSTM from the observed values in 2009 and 2014.
表 2 展示了 LSTM 模型和 VMD-LSTM 模型对未来一天 F10.7 指数的预测结果。VMD-LSTM 模型的 RMSE 低于 LSTM 模型,在第 24 太阳活动周期间,VMD-LSTM 的平均 RMSE 为 4.47 sfu,而 LSTM 的平均 RMSE 为 5.71 sfu,这表明 VMD-LSTM 的 RMSE 降低了 21.72%。此外,在相关系数方面,VMD-LSTM 模型也表现出优于 LSTM 模型的性能,在整个太阳活动周内的相关系数达到 0.99,证明了 VMD-LSTM 模型在预测 F10.7 指数方面的有效性。
Table 2. Prediction Results of Long Short-Term Memory and Variational Mode Decomposition Algorithm-Long Short Term Memory Neural Network for the F10.7 Index in Solar Cycle 24
Year RMSE R LSTM VMD-LSTM Error reduction (%) LSTM VMD-LSTM 2009 1.13 0.89 21.24 0.93 0.95 2010 2.53 1.72 32.02 0.91 0.94 2011 5.53 4.56 17.54 0.97 0.98 2012 7.13 5.40 24.26 0.93 0.96 2013 6.17 4.66 24.47 0.97 0.97 2014 9.89 8.20 17.09 0.94 0.95 2015 9.57 7.32 23.51 0.88 0.93 2016 3.76 2.60 30.85 0.96 0.97 2017 5.57 3.85 30.88 0.89 0.94 2018 1.21 0.89 26.45 0.93 0.96 2019 1.21 0.90 25.62 0.91 0.95 All 5.71 4.47 21.72 0.98 0.99
模型在高太阳活动期间预测 F10.7 指数的性能如何呢?
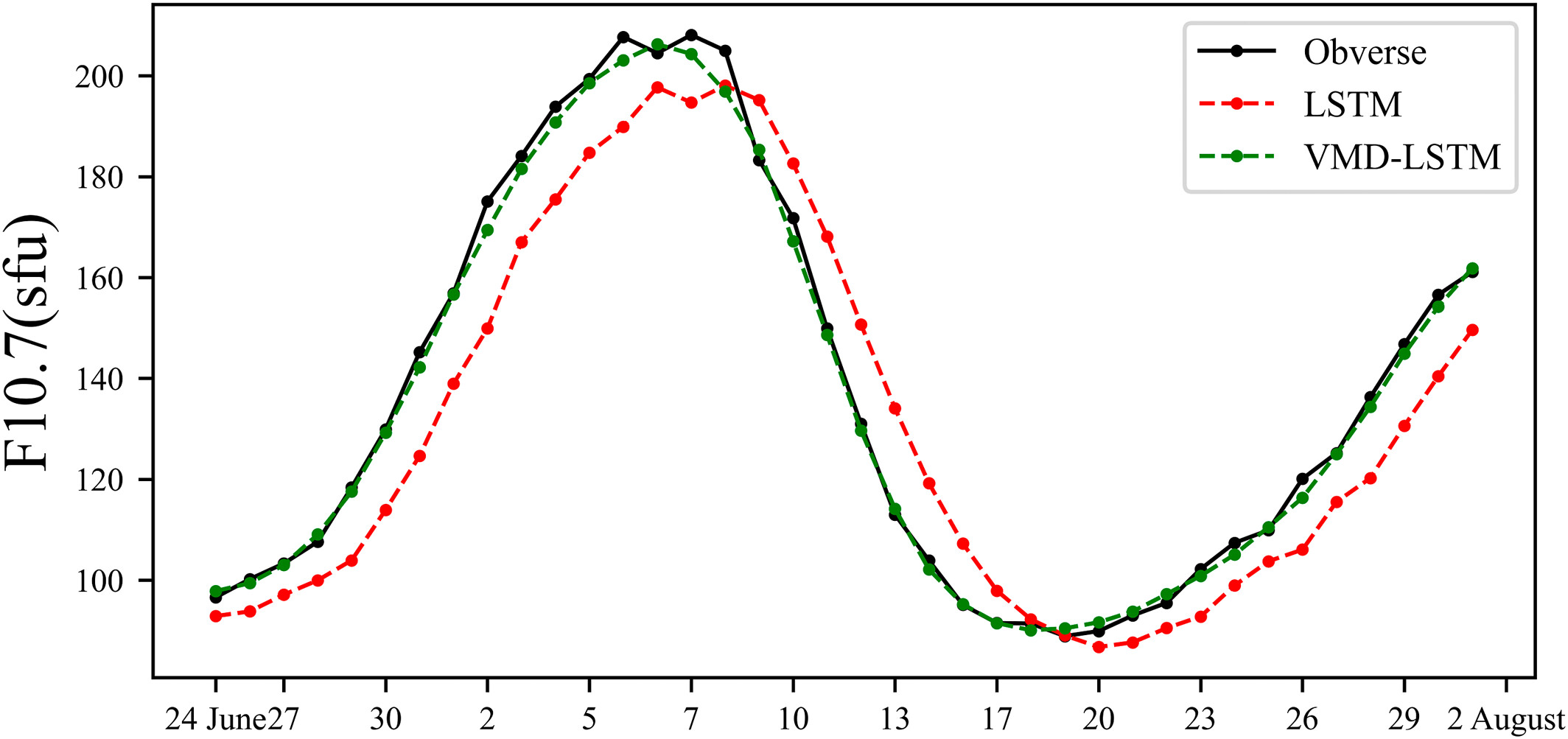
这里,选取了 2014 年 6 月 24 日至 8 月 2 日期间的 F10.7 指数案例进行分析。图 8 显示了在此期间两种模型(LSTM, VMD-LSTM)的预测结果与观测结果的对比。如图 6 所示,VMD-LSTM 模型的预测值在大多数点上更接近 F10.7 指数的观测值。这表明 VMD 可以有效提高预测能力,并且 VMD-LSTM 模型能够基于训练集样本信息的分析,准确预测 F10.7 指数的后续值。
Figure 8
The comparison of the Variational Mode Decomposition algorithm-Long Short Term Memory Neural Network model prediction with the observations from 24 June to 2 August 2014.
3.3 Compared Results
为了更好地评估 VMD-LSTM 模型的预测性能,本文将其结果与 LSTM 模型 (W. Zhang et al., 2022)、BP 模型 (Xiao et al., 2017) 和 AR 模型 (Du, 2020) 的结果进行了比较。BP 模型使用输出误差来估计输出层中直接前导层的误差,然后用该误差估计前一层的误差。重复此过程以获得所有其他层的误差估计。AR 模型利用预测目标的历史时间序列与其在不同时期的值之间的依赖关系建立回归方程进行预测。LSTM 模型通过引入记忆单元和三个门控机制(遗忘门、输入门和输出门)来解决长期依赖问题。记忆单元负责存储序列信息,三个门控机制控制记忆单元的读取、写入和保留程度。这三种模型通常用于处理时间序列。与前两种神经网络模型不同,AR 模型是一种专为处理时间序列数据而设计的统计方法。结果如表 3 所示,VMD-LSTM 模型在大多数年份的 RMSE 值低于 LSTM、AR 和 BP 模型,表明其在预测 F10.7 指数方面具有强大的性能。然而,在某些年份,VMD-LSTM 模型的性能可能略逊于其他模型,这可能是由于数据的特定特征所致。需要进一步的研究和分析来探讨这一点。
Table 3. Comparison of Root Mean Square Error Between the Variational Mode Decomposition Algorithm-Long Short Term Memory Neural Network and Other Models (1-Day Prediction)
Year VMD-LSTM LSTM BP AR 2009 0.89 1.20 1.07 – 2010 1.72 – – – 2011 4.56 5.52 – 5.29 2012 5.40 – – – 2013 4.66 – – – 2014 8.20 9.40 – 7.92 2015 7.32 – – – 2016 2.60 3.23 – 2.99 2017 3.85 – – – 2018 0.89 – – – 2019 0.90 1.36 – 1.27
此外,本文应用相同的方法对 F10.7 指数进行了 7 天预测,结果总结在表 4 中。该表清楚地表明,VMD-LSTM 模型生成的 7 天预测结果优于 SWPC 以及 Gao 等人 (2022) 最近开发的具有多输入的 LSTM 模型(M-LSTM)。在 Gao 等人的研究中,LSTM 方法基于其线性关系用于 F10.7 的 7 天预测。在 2009 年至 2019 年期间,VMD-LSTM 模型的 RMSE 始终显著低于 M-LSTM 和 SWPC 模型,这证实了其为 F10.7 指数提供高精度 7 天预测的能力。值得注意的是,在 2014 年,VMD-LSTM 模型的 RMSE 与 M-LSTM 模型非常接近,但 VMD-LSTM 模型仍保持轻微优势,突显了其在 7 天预测中的竞争优势。总之,VMD-LSTM 模型在预测 F10.7 指数的 7 天预报方面表现出卓越的性能,特别是与其他模型相比时。这一进展对太阳活动和空间天气预报的准确预测具有重要意义。
Table 4. Comparison of Root Mean Square Error Between the Variational Mode Decomposition Algorithm-Long Short Term Memory Neural Network and Other Models (7-Day Prediction)
Year RMSE VMD-LSTM M-LSTM SWPC 2009 1.82 2.40 2.37 2010 4.51 5.28 5.35 2011 7.63 15.82 17.57 2012 7.97 16.60 17.71 2013 9.95 18.22 19.86 2014 11.75 23.31 – 2015 9.71 19.94 – 2016 4.46 8.95 – 2017 5.24 11.46 – 2018 1.29 2.89 – 2019 1.25 2.62 –
4 Summary
本研究提出了一种VMD-LSTM模型用于F10.7的短期预测,该模型将VMD算法与LSTM网络相结合。首先,应用VMD算法将F10.7数据分解为多个子分量,然后使用LSTM网络对每个子分量进行预测。最后,将各子分量的预测值求和得到最终的F10.7指数预测值。本文将VMD-LSTM模型的性能与LSTM、AR和BP模型进行了比较。结果表明,VMD-LSTM模型在预测精度上优于LSTM、AR和BP模型。具体而言,在第24太阳活动周期间,VMD-LSTM模型每年的RMSE和R值均优于同年的LSTM模型。在整个太阳活动周期间,LSTM模型的RMSE和R值分别为5.71和0.98,而VMD-LSTM模型的RMSE和R值分别为4.47和0.99,RMSE降低了21.72%。VMD-LSTM模型的高精度归因于VMD算法在有效降低F10.7数据序列的非线性和复杂性方面的作用,这有助于LSTM网络捕捉序列变化的内部规律。
遗憾的是,提出的模型目前无法实现实时预测。在未来,无法对未知数据进行分解以实现实时预测过程。因此,有必要使用滚动预测方法 (rolling forecast methods):每次预测一个数据点,然后将该数据点添加到已知的历史数据中。接着使用新的历史数据预测下一个数据点,并依此重复该过程。同时,也需要持续更新预测模型中的参数以逐步适应新的输入。此外,可以参考Stevenson等人的工作(Stevenson et al., 2022),将VMD-LSTM模型用于中期预报。