当前位置：首页 > news >正文

CSP认证准备第四天-BFS（双端BFS/0-1BFS）和DFS

news 来源：原创 2025/6/4 21:32:30

B. Chamber of Secrets

参考资料：

问题 - 173B - Codeforces

还是上次那到题目，纯看代码有点看不懂，让ai解释一下：

add_front：将状态添加到队列前端（用于不增加代价的移动）
add_back：将状态添加到队列后端（用于增加代价的移动）

void add_front(int x, int y, int dir, int d) {if (d < dist[x][y][dir]) {      //只有当我们找到更小的 d 时才需要更新 dist 和加入队列dist[x][y][dir] = d;q.push_front(dir);q.push_front(y);q.push_front(x);}
}void add_back(int x, int y, int dir, int d) {if (d < dist[x][y][dir]) {dist[x][y][dir] = d;q.push_back(x);q.push_back(y);q.push_back(dir);}
}

双端队列BFS：处理0-1权重图的最短路径问题，0代价的操作放队首，1代价的操作放队尾。
状态表示：使用三维数组dist[x][y][dir]记录到达位置(x,y)时方向为dir的最小代价。
反向搜索：从终点开始搜索到起点，与正向搜索等价但实现上更方便。

BFS主循环：

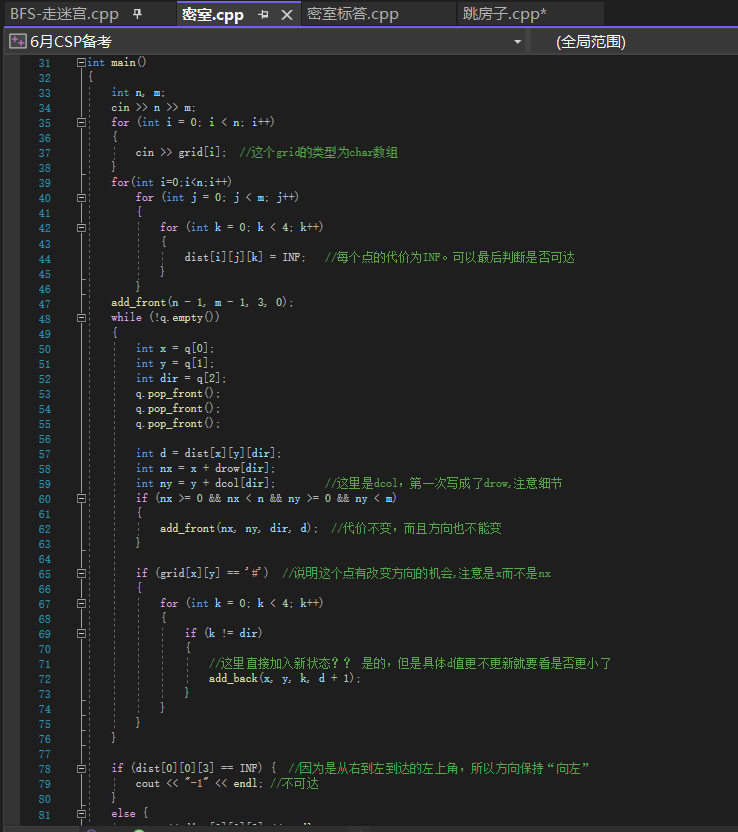
while (!q.empty()) {int x = q[0], y = q[1], dir = q[2];q.pop_front(); q.pop_front(); q.pop_front();int d = dist[x][y][dir];// 尝试沿当前方向移动（不改变方向，不增加代价）int nx = x + fx[dir], ny = y + fy[dir];if (nx >= 0 && nx < n && ny >= 0 && ny < m)add_front(nx, ny, dir, d);// 如果当前格子是障碍物，可以改变方向（增加1代价）if (grid[x][y] == '#')for (int i = 0; i < 4; i++)if (i != dir) add_back(x, y, i, d + 1);
}

这道题让我疑惑的就是方向，注意这里的坐标原点为左上角，所以如果x不变，y-1，是往左移动的。不要受x、y命名的影响,这里x就是行，y就是列，行号不变，列号减小就是往左移动。完整代码：

#include <deque>
#include <iostream>
using namespace std;constexpr int INF = 1 << 29;  // 定义无穷大值，表示不可达
int n, m;                     // 网格的行数和列数
char grid[1001][1001];        // 存储网格数据，'#'表示障碍物，'.'表示空地// dist[x][y][dir] 表示到达位置(x,y)且方向为dir时的最小代价
int dist[1001][1001][4];// 四个方向的移动增量：下、上、右、左
int fx[] = {1, -1, 0, 0};
int fy[] = {0, 0, 1, -1};deque<int> q;  // 双端队列，用于实现0-1 BFSvoid add_front(int x, int y, int dir, int d) {// 只有找到更小的代价时才更新if (d < dist[x][y][dir]) {dist[x][y][dir] = d;  // 更新最小代价// 将状态压入队列前端（x、y、dir三个值）// 注意顺序：先压dir，最后压x，这样取出时顺序就是x,y,dirq.push_front(dir);q.push_front(y);q.push_front(x);}
}void add_back(int x, int y, int dir, int d) {if (d < dist[x][y][dir]) {dist[x][y][dir] = d;// 将状态压入队列后端（x、y、dir三个值）q.push_back(x);q.push_back(y);q.push_back(dir);}
}int main() {// 读取输入cin >> n >> m;for (int i = 0; i < n; i++) {cin >> grid[i];}// 初始化距离数组为无穷大for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {for (int k = 0; k < 4; k++) {dist[i][j][k] = INF;}}}// 从终点(n-1,m-1)开始搜索，初始方向为左(3)，代价为0add_front(n - 1, m - 1, 3, 0);// 开始双端队列BFSwhile (!q.empty()) {// 取出队首状态int x = q[0];int y = q[1];int dir = q[2];q.pop_front();q.pop_front();q.pop_front();int d = dist[x][y][dir];  // 当前状态的代价// 尝试沿当前方向移动（不改变方向，不增加代价）int nx = x + fx[dir];int ny = y + fy[dir];// 检查新位置是否在网格内if (nx >= 0 && nx < n && ny >= 0 && ny < m) {// 将新状态加入队首（代价不变）add_front(nx, ny, dir, d);}// 如果当前格子是障碍物，可以改变方向（需要花费1代价）if (grid[x][y] == '#') {// 尝试所有其他三个方向for (int i = 0; i < 4; i++) {if (i != dir) {// 将新状态加入队尾（代价+1）add_back(x, y, i, d + 1);}}}}// 输出结果：起点(0,0)方向为左(3)的最小代价if (dist[0][0][3] == INF) {cout << -1 << endl;  // 不可达} else {cout << dist[0][0][3] << endl;  // 输出最小代价}return 0;
}

第36次CCF认证-第四题

相关文件： TUOJ

参考题解：

CCF-CSP第36次认证第四题——跳房子【NA！巧妙利用BFS】_csp跳房子-CSDN博客

第36次ccf-csp题解（思维） - devoteeing - 博客园

感觉学完BFS之后，这道题并不难。和模版差不了多少，就是隔了一个n,如果遍历的时候，下一个位置为n，则可以提前结束循环。

#include <bits/stdc++.h>
using namespace std;
int main()
{int n;scanf("%d", &n);vector<int> a(n + 1);vector<int> k(n + 1);vector<int> step(n + 1, -1);step[1] = 0;queue<int> q;q.push(1); //先把第一个位置push进去for (int i = 1; i <= n; i++){scanf("%d", &a[i]);}for (int i = 1; i <= n; i++){scanf("%d", &k[i]);}while (!q.empty()){int x = q.front();q.pop();if (x == n) break; //已经到达终点n,可以提前跳出，可以避免超时？int l = x + 1;  //跳跃区间最左侧int r = min(n, x + k[x]);   //跳跃区间最右侧if (r == n) {step[n] = step[x] + 1;break;}for (int i = r; i >= l; i--)   //从右往左遍历{int next = i - a[i];             //注意还需要往回退if (step[next] == -1)  //说明还没有遍历到{step[next] = step[x] + 1;q.push(next);       //注意是在这里push的，而不是在for循环里push}                            //注意BFS的特点，一旦遍历到了某个节点，这个节点的距离就是最小的，定死了。}}cout << step[n];return 0;
}

这个版本的代码超时了，只拿到了30分

另一篇满分题解：

代码中使用了BFS，但是与之前不同，它引入了一个变量pos来记录当前已经处理到的最远位置（即已经处理过的位置能够到达的最右端），从而避免重复处理。

这段代码中利用pos来记录当前已经处理过的最远位置。在以后每次处理中，只处理新出现的区间（pos,x+k[x]）,避免重复遍历。

#include <bits/stdc++.h>
//#define int long long
using namespace std;
void ooo(int x){cout<<x<<'\n';
}
struct p{int id, num;
};
const int xmmm=2e5+10;
int a[xmmm], b[xmmm], k[xmmm];
int dis[xmmm];
bool vis[xmmm];
signed main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=i-a[i];}for(int i=1;i<=n;i++)cin>>k[i];int pos=0;queue<p>q;//q.clear();q.push(p{1, 0});int ans=-1;while(!q.empty()){p t=q.front();q.pop();if(vis[t.id])continue;vis[t.id]=1;if(t.id==n){ans=t.num;break;}int x=t.id;if(x+k[x]<=pos)continue;if(x+k[x]>=n){q.push(p{n, t.num+1});continue;}for(int i=max(pos+1, x+1);i<=min(n, x+k[x]);i++){q.push(p{b[i], t.num+1});}pos=max(pos, x+k[x]);}cout<<ans<<'\n';return 0;
}
/*5
0 1 2 3 0
3 4 4 10 1510
0 1 1 1 1 3 1 0 3 0
2 4 5 4 1 4 1 3 5 3
*/

借这个思路，我们在原有代码基础上进行优化，引入max_covered变量，也就是上述代码中的pos。只需要修改一点点，降低算法复杂度：

#include <bits/stdc++.h>
using namespace std;
const long long N=1e5 + 2;
int main()
{int n;scanf("%d", &n);int a[N];int k[N];vector<int> step(n + 1, -1);step[1] = 0;queue<int> q;q.push(1); //先把第一个位置push进去int max_covered = 0;for (int i = 1; i <= n; i++){cin>>a[i];}for (int i = 1; i <= n; i++){cin>>k[i];}while (!q.empty()){int x = q.front();q.pop();if (x == n) break; //已经到达终点n,可以提前跳出，可以避免超时？int l = x + 1;  //跳跃区间最左侧int r = min(n, x + k[x]);   //跳跃区间最右侧if (r == n) {step[n] = step[x] + 1;break;}if (r <= max_covered) continue;for (int i = r; i >= max(l,max_covered); i--)   //从右往左遍历{int next = i - a[i];             //注意还需要往回退if (step[next] == -1)  //说明还没有遍历到{step[next] = step[x] + 1;q.push(next);       //注意是在这里push的，而不是在for循环里push}                            //注意BFS的特点，一旦遍历到了某个节点，这个节点的距离就是最小的，定死了。}max_covered = r;         }cout << step[n];return 0;
}

成功通过：

第36次CCF认证-第二题

这道题我记得，当时我在考场上推了半天来着，最后好像是拿到了80的部分分。

原文件：TUOJ

还是参考这个博主的题解：第36次ccf-csp题解（思维） - devoteeing - 博客园

好吧，看到“负数”这个概念让我想起来这道题笔者上一篇帖子有复习过，但是隔得时间太久了，忘记了┭┮﹏┭┮。我再去复习一下。

ps:之前没有提交题解到系统，这次发现居然这个题解也超时了，笔者当时就是因为超时扣的20呜呜呜，看来还是得看一下别的题解。

这个大佬的题解能通过：第36次ccf-csp题解（思维） - devoteeing - 博客园

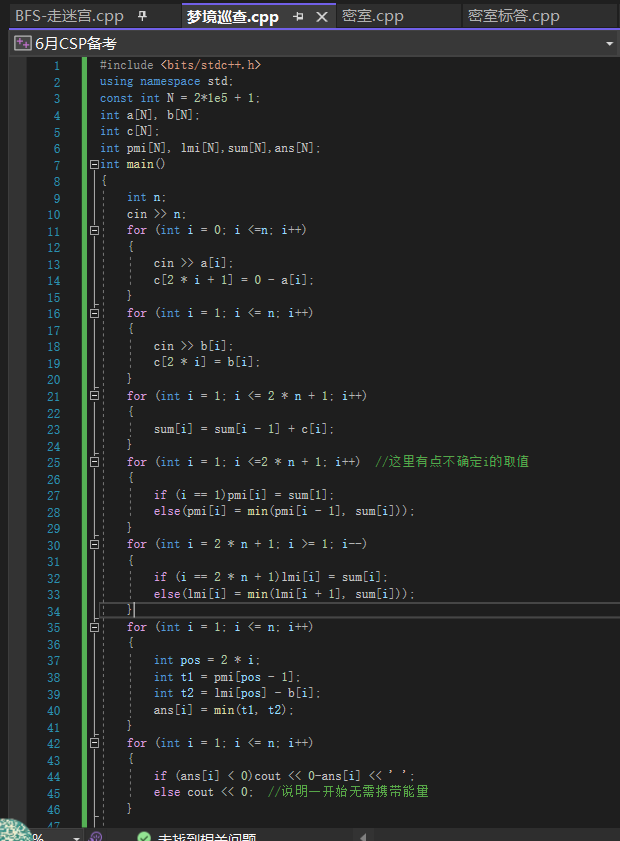
关键在于怎样维护bi=0时，全程中所拥有补给的最小量（为负数表示还需要多少补给）所以就是一个单点修改，以bi为分界处，维护前半段和后半段最小值，对两段最小值取最小值，为负数则取绝对值，为非负数则为0。注意后半段的值还需要带上b[i]，然后再对前半段和后半段进行比较。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int xmmm=2e5+10;
int a[xmmm], b[xmmm];
int c[xmmm];
int sum[xmmm];
int pmi[xmmm], lmi[xmmm];
int ans[xmmm];
void ooo(int x){cout<<x<<'\n';
}
signed main()
{int n;cin>>n;for(int i=0;i<=n;i++){cin>>a[i];c[i*2+1]=0-a[i];}for(int i=1;i<=n;i++){cin>>b[i];c[i*2]=b[i];}pmi[0]=lmi[2*n+2]=0-1e10;for(int i=1;i<=2*n+1;i++){sum[i]=sum[i-1]+c[i];}for(int i=1;i<=2*n+1;i++){if(i==1)pmi[i]=sum[i];else pmi[i]=min(pmi[i-1], sum[i]);}for(int i=2*n+1;i>=1;i--){if(i==2*n+1)lmi[i]=sum[i];else lmi[i]=min(lmi[i+1], sum[i]);}for(int i=1;i<=n;i++){int pos=i*2;int t1=pmi[pos-1];int t2=lmi[pos]-b[i];ans[i]=min(t1, t2);}for(int i=1;i<=n;i++){if(ans[i]<0)cout<<0-ans[i]<<' ';else cout<<0<<' ';}return 0;
}
/*3
5 5 5 5
0 100 039 4 6 2
9 4 6
*/

看完这篇题解我在思考，有没有可能将最开始那篇题解做一个优化，引入前缀和，能否解决超时的问题？应该是不行的，如果保留之前那个思路，遍历每一个b[i]依次再进行处理，应该是会超时的。