【MPC控制 - 从ACC到自动驾驶】车辆纵向动力学建模与离散化：MPC的“数字蓝图”

【MPC控制 - 从ACC到自动驾驶】车辆纵向动力学建模与离散化：MPC的“数字蓝图”

昨天我们聊了ACC是什么，以及MPC这个“深谋远虑的棋手”是如何思考问题的。我们知道MPC的“P”代表“Prediction”（预测），而预测未来的前提，是你得知道事物是如何发展的，对吧？就像天气预报员需要大气模型，我们控制汽车，就需要汽车的模型。今天，我们就来给我们的ACC系统，量身打造一个合适的“汽车行为说明书”——也就是车辆的纵向动力学模型。

在正式开始之前，我们先思考一个问题：为什么建模这么重要？

想象一下，你是一位大厨，想做一道绝世美味。你脑子里有对这道菜最终味道的完美构想（对应MPC的优化目标），你也知道手边有哪些食材和调料（对应汽车的物理限制和控制输入）。但是，如果你不知道每种食材在煎炒烹炸之下会发生什么味道和质地的变化（缺乏模型），那你怎么能精确地调配，最终做出那道完美的菜肴呢？

同样，MPC要想做出最优的控制决策（比如给多大的油门或刹车），它必须能够预测出，在这些决策下，我们的车辆在未来几秒钟内会如何运动——速度会变成多少？与前车的距离会变成多少？而这种预测能力的基石，就是车辆动力学模型。没有模型，MPC就成了“无米之炊”的巧妇，空有算法也无从下手。

所以，今天我们的核心任务就是：

1. 理解车辆在前进和后退（纵向）方向上是如何运动的。
2. 学习如何用数学语言（状态空间方程）来描述这种运动。
3. 将这种连续的数学描述，转化为计算机能够理解和处理的离散形式。

车辆纵向动力学：汽车是如何前进和后退的？

我们这里关注的是“纵向”动力学，简单来说，就是汽车前进和后退的运动规律，暂时不考虑转弯（那是横向动力学的事儿，以后有机会再聊）。

想象一下你在开车：

• 踩油门，发动机输出驱动力，车子加速前进。
• 踩刹车，制动系统产生制动力，车子减速。
• 即使不踩油门也不踩刹车，车子也不会永远跑下去，因为有空气阻力、轮胎与地面的滚动阻力，它们会使车子慢慢停下来。
• 如果在上坡，还需要克服坡道阻力；下坡则相反，坡道会“推”你一把。

这些力共同决定了汽车的加速度，进而决定了它的速度和位置。这背后的基本原理，就是我们中学物理学过的牛顿第二定律：

$F_{合}=m\cdot a$

其中：

• $F_{合}$ 是作用在汽车上的合外力（沿行驶方向）。
• $m$ 是汽车的质量。
• $a$ 是汽车的加速度。

简化一下：抓住主要矛盾

真实的车辆受力非常复杂，如果把所有因素都考虑进去，模型会变得异常庞大和难以处理，对于ACC控制来说，有点“杀鸡用牛刀”了。在工程实践中，我们通常会做一些合理的简化，抓住影响车辆纵向运动的主要因素。

对于ACC场景，我们通常做如下简化假设：

1. 平直道路： 暂时不考虑坡道阻力和转弯时的侧向力影响。这意味着我们主要关注驱动力/制动力、空气阻力和滚动阻力。
2. 忽略传动系统动态： 我们假设发动机/电机和刹车系统能够比较快地响应我们的加速度请求。也就是说，我们不直接控制油门开度和刹车压力，而是假设有一个底层的控制器，能够根据我们给出的“期望加速度”指令，来精确地产生这个加速度。这大大简化了上层ACC控制器的设计。
3. 空气阻力和滚动阻力模型简化：
   • 空气阻力 $F_{air}$ 通常与车速的平方成正比：$F_{air}=\frac{1}{2}\rho C_{d}A{v}^2$，其中 $\rho$ 是空气密度，$C_d$ 是风阻系数，$A$ 是迎风面积，$v$ 是车速。为了简化，有时会将其线性化处理，或者在特定工作点附近近似。
   • 滚动阻力 $F_{roll}$ 通常与车辆重力垂直于地面的分量成正比：$F_{roll}=C_{r}mg\cos (\theta )$，其中 $C_r$ 是滚动阻力系数，$g$ 是重力加速度，$\theta$ 是坡度角。在平路上 $\cos (\theta )\approx 1$，所以 $F_{roll}\approx C_{r}mg$。

在最简化的模型中，我们甚至可以把空气阻力和滚动阻力的综合影响，以及一些未建模的扰动，都归结为一个与车速相关的阻滞项，或者在设计控制器时通过积分作用来补偿它们。

对于我们ACC的MPC控制器来说，最关心的输入是本车的期望加速度 $a_{ego}$，最关心的状态是本车的速度 $v_{ego}$ 和与前车的相对距离 $d_{rel}$。

状态空间模型：给汽车运动规律安个“家”

好了，我们对汽车的受力有了基本了解。现在，我们需要一种标准的、系统化的数学工具来描述它的运动。在现代控制理论中，状态空间表示法（State-Space Representation） 就是这样一种强大的工具。它非常适合描述多输入多输出（MIMO）系统，也方便计算机进行分析和计算。

状态空间模型通常由两个方程组成：

1. 状态方程 (State Equation): 描述系统状态如何随时间变化。
   $\dot{\mathbf{x}}(t)=\mathbf{Ax}(t)+\mathbf{B}u(t)+{\mathbf{B}}_{w}w(t)$
2. 输出方程 (Output Equation): 描述系统的输出与状态和输入之间的关系。
   $\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{D}u(t)$

是不是看到一堆字母和矩阵有点晕？别急，我们一个个来解释：

• $\mathbf{x}(t)$: 状态向量 (State Vector)。它是一组能够完全描述系统在任意时刻 $t$ 内部状态的最小变量集合。对于我们的ACC问题，状态可以包括本车速度、与前车的相对距离、前车速度等。带点的 $\dot{\mathbf{x}}(t)$ 表示状态向量对时间的导数，即状态的变化率。
• $u(t)$: 控制输入 (Control Input)。这是我们能够施加给系统的控制信号。在ACC中，这通常是我们期望的本车加速度 $a_{ego}$。
• $w(t)$: （可测或不可测）扰动 (Disturbance)。例如前车的加速度 $a_{lead}$，我们可以通过雷达测量前车速度变化来估计它，它会影响我们的状态，但不是我们直接控制的。
• $\mathbf{y}(t)$: 输出向量 (Output Vector)。这是我们关心的、希望控制或者需要观测的系统量。在ACC中，输出通常就是相对距离 $d_{rel}$ 和本车速度 $v_{ego}$。
• $\mathbf{A}$: 系统矩阵 (System Matrix)。描述系统内部状态之间的相互影响。如果A的某个元素非零，说明对应的两个状态变量之间存在耦合。
• $\mathbf{B}$: 输入矩阵 (Input Matrix)。描述控制输入如何影响系统状态的变化。
• ${\mathbf{B}}_w$: 扰动矩阵 (Disturbance Matrix)。描述扰动如何影响系统状态的变化。
• $\mathbf{C}$: 输出矩阵 (Output Matrix)。描述如何从系统状态中得到我们关心的输出量。
• $\mathbf{D}$: 前馈矩阵 (Feedthrough Matrix)。描述控制输入如何直接影响输出（不经过状态的动态变化）。在很多物理系统中，$\mathbf{D}$ 常常是零矩阵。

这套方程就像是给汽车的运动规律找到了一个结构化的“家”。我们只需要确定状态是什么，输入是什么，输出是什么，然后把它们之间的关系用A, B, C, D这些矩阵表达出来，一个描述汽车行为的“说明书”就完成了。

构建ACC的“三驾马车”状态空间模型

现在，让我们具体为ACC场景构建一个常用的状态空间模型。这个模型通常被称为“三驾马车”模型，因为它关注三个核心动态变量：

1. 本车速度 ($v_{ego}$): 这是我们直接控制的结果。
2. 本车与前车的相对距离 ($d_{rel}$): 这是ACC安全性的核心。$d_{rel}=x_{lead}-x_{ego}$，其中 $x_{lead}$ 是前车车尾位置，$x_{ego}$ 是本车车头位置。
3. 前车速度 ($v_{lead}$): 这是影响相对距离变化的关键外部因素。

让我们来定义状态向量、控制输入和输出：

• 状态向量 $\mathbf{x}(t)$:
  $$\mathbf{x}(t)=\left[\begin{array}{c}{v}_{ego}(t)\\ d_{rel}(t)\\ v_{lead}(t)\end{array}\right]$$
  这里，我们选择这三个量作为状态。为什么是它们？因为它们能比较完整地描述ACC跟驰场景下的主要动态，并且它们的变化规律也相对容易用物理方程表达。

• 控制输入 $u(t)$:
  $u(t)=a_{ego}(t)$
  即本车的期望加速度（或实际产生的加速度，假设底层控制器能完美跟踪）。

• 可测扰动 $w(t)$:
  $w(t)=a_{lead}(t)$
  即前车的加速度。我们假设可以通过传感器（如雷达）数据对前车速度进行求导来估计得到前车的加速度。这个量会影响 $v_{lead}$ 的变化，进而影响 $d_{rel}$。

• 输出向量 $\mathbf{y}(t)$:
  我们最关心的是相对距离和本车速度，所以：
  $$\mathbf{y}(t)=\left[\begin{array}{c}{d}_{rel}(t)\\ v_{ego}(t)\end{array}\right]$$

接下来，我们要推导状态方程 $\dot{\mathbf{x}}(t)=\mathbf{Ax}(t)+\mathbf{B}u(t)+{\mathbf{B}}_{w}w(t)$ 中的A, B, $B_w$ 矩阵，以及输出方程 $\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{D}u(t)$ 中的C, D矩阵。

1. ${\dot{v}}_{ego}(t)$ (本车速度的变化率):
   本车速度的变化率就是本车的加速度。我们假设本车的实际加速度 $a_{ego}$ 就是我们的控制输入 $u(t)$。
   ${\dot{v}}_{ego}(t)=a_{ego}(t)=u(t)$
   所以，在状态方程的第一行，它只与 $u(t)$ 有关。

2. ${\dot{d}}_{rel}(t)$ (相对距离的变化率):
   相对距离 $d_{rel}=x_{lead}-x_{ego}$。对时间求导：
   ${\dot{d}}_{rel}(t)={\dot{x}}_{lead}(t)-{\dot{x}}_{ego}(t)=v_{lead}(t)-v_{ego}(t)$
   所以，在状态方程的第二行，它与 $v_{lead}(t)$ 和 $v_{ego}(t)$ 有关。

3. ${\dot{v}}_{lead}(t)$ (前车速度的变化率):
   前车速度的变化率就是前车的加速度 $a_{lead}(t)$，也就是我们的扰动 $w(t)$。
   ${\dot{v}}_{lead}(t)=a_{lead}(t)=w(t)$
   所以，在状态方程的第三行，它只与 $w(t)$ 有关。

根据以上推导，我们可以写出状态方程的矩阵形式：
$$\left[\begin{array}{c}{\dot{v}}_{ego}(t)\\ {\dot{d}}_{rel}(t)\\ {\dot{v}}_{lead}(t)\end{array}\right]=\underset{\mathbf{A}}{\underbrace{\left[\begin{array}{ccc}0& 0& 0\\ -1& 0& 1\\ 0& 0& 0\end{array}\right]}}\left[\begin{array}{c}{v}_{ego}(t)\\ d_{rel}(t)\\ v_{lead}(t)\end{array}\right]+\underset{\mathbf{B}}{\underbrace{\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]}}u(t)+\underset{{\mathbf{B}}_w}{\underbrace{\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]}}w(t)$$

再来看输出方程 $\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{D}u(t)$:
我们定义的输出是 $y_1(t)=d_{rel}(t)$ 和 $y_2(t)=v_{ego}(t)$。
$d_{rel}(t)$ 就是状态向量中的第二个元素。
$v_{ego}(t)$ 就是状态向量中的第一个元素。
输出与当前控制输入 $u(t)$ 没有直接关系（即加速度不会瞬间改变距离或速度，而是通过积分效应改变）。所以 $\mathbf{D}$ 矩阵是零矩阵。

因此，输出方程的矩阵形式是：
$$\left[\begin{array}{c}{d}_{rel}(t)\\ v_{ego}(t)\end{array}\right]=\underset{\mathbf{C}}{\underbrace{\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\end{array}\right]}}\left[\begin{array}{c}{v}_{ego}(t)\\ d_{rel}(t)\\ v_{lead}(t)\end{array}\right]+\underset{\mathbf{D}}{\underbrace{\left[\begin{array}{c}0\\ 0\end{array}\right]}}u(t)$$

融会贯通一下：

• A 矩阵告诉我们：
  • ${\dot{v}}_{ego}$ 不直接依赖于任何当前状态（在这个简化模型中，它的变化只来自输入 $u(t)$）。
  • ${\dot{d}}_{rel}$ (相对速度) 等于 $v_{lead}-v_{ego}$。
  • ${\dot{v}}_{lead}$ 不直接依赖于任何当前状态（它的变化只来自扰动 $w(t)$）。
• B 矩阵告诉我们：控制输入 $u(t)$ (即 $a_{ego}$) 只直接影响 ${\dot{v}}_{ego}$。
• $B_w$ 矩阵告诉我们：扰动 $w(t)$ (即 $a_{lead}$) 只直接影响 ${\dot{v}}_{lead}$。
• C 矩阵告诉我们：我们观测的第一个输出是状态 $d_{rel}$，第二个输出是状态 $v_{ego}$。
• D 矩阵是零，表示控制输入 $u(t)$ 不会瞬时地、直接地出现在输出 $\mathbf{y}(t)$ 中。

至此，我们就为ACC系统建立了一个连续时间的状态空间模型！这个模型虽然简单，但抓住了核心的动态关系，是后续MPC控制器设计的重要基础。

模型离散化：让计算机看懂“连续”的世界

我们刚刚建立的状态空间模型是连续时间 (Continuous-Time) 的，因为时间变量 $t$ 是连续变化的，状态的导数 $\dot{\mathbf{x}}(t)$ 也是瞬时变化率。但是，我们的MPC控制器最终是要在数字计算机上运行的。数字计算机处理信息的方式是离散的，它不能处理无限精细的连续信号，而是以固定的时间间隔（称为采样时间 $T_s$）对信号进行采样和计算。

这就好比看电影，电影胶片本身是一格一格的静态图片（离散的），但因为播放速度足够快（采样频率足够高），我们就感觉画面是连续运动的。

因此，我们需要把连续时间的状态空间模型，转换成离散时间 (Discrete-Time) 的状态空间模型。这个过程就叫做模型离散化 (Discretization)。

离散时间状态空间模型通常写成这样：
$\mathbf{x}(k+1)={\mathbf{A}}_d\mathbf{x}(k)+{\mathbf{B}}_{d}u(k)+{\mathbf{B}}_{wd}w(k)$
$\mathbf{y}(k)={\mathbf{C}}_d\mathbf{x}(k)+{\mathbf{D}}_{d}u(k)$

这里的符号意义：

• $k$: 表示离散的时间步长，而不是连续的时间 $t$。例如，$k=0,1,2,...$
• $\mathbf{x}(k)$: 在第 $k$ 个采样时刻的系统状态。
• $u(k)$: 在第 $k$ 个采样时刻施加的控制输入（通常假设在 $k$ 到 $k+1$ 这个采样周期内保持不变）。
• $w(k)$: 在第 $k$ 个采样时刻的扰动。
• ${\mathbf{A}}_d,{\mathbf{B}}_d,{\mathbf{B}}_{wd},{\mathbf{C}}_d,{\mathbf{D}}_d$: 它们是离散时间模型对应的系统矩阵、输入矩阵、扰动矩阵、输出矩阵和前馈矩阵。它们的值与连续时间模型的 $\mathbf{A},\mathbf{B},{\mathbf{B}}_w,\mathbf{C},\mathbf{D}$ 以及采样时间 $T_s$ 都有关系。

离散化的方法：零阶保持器 (ZOH)

将连续模型转化为离散模型有很多种方法，比如前向欧拉法、后向欧拉法、双线性变换（Tustin变换）等。在控制系统中最常用，也是MATLAB等工具中 c2d (continuous to discrete) 函数默认使用的方法之一，叫做零阶保持器 (Zero-Order Hold, ZOH) 方法。

ZOH方法基于一个非常自然的假设：在一个采样周期 $T_s$ 内（即从时刻 $k{T}_s$ 到 $(k+1)T_s$），计算机发出的控制信号 $u(k{T}_s)$ 是保持不变的。 就像楼梯一样，每个台阶的高度在一定宽度内是不变的。

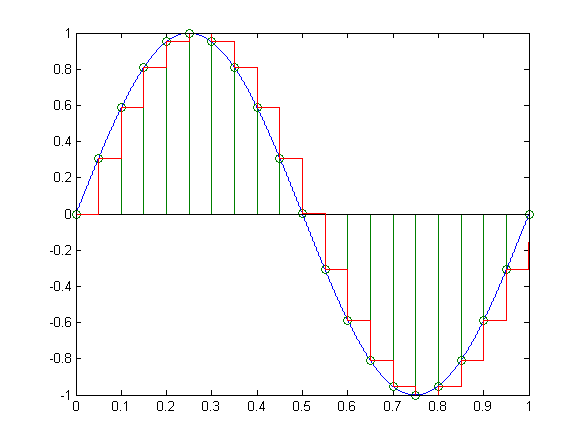
基于这个假设，可以从连续时间状态方程精确地推导出离散时间状态方程的矩阵。对于线性时不变系统 $\dot{\mathbf{x}}(t)=\mathbf{Ax}(t)+\mathbf{B}u(t)$ (暂时忽略扰动 $w(t)$，其处理方式类似)，其在ZOH下的离散化公式为：

${\mathbf{A}}_d=e^{\mathbf{A}{T}_s}$
${\mathbf{B}}_d=\left({\int }_0^{T_s}{e}^{\mathbf{A}\tau }d\tau \right)\mathbf{B}={\mathbf{A}}^{-1}(e^{\mathbf{A}{T}_s}-\mathbf{I})\mathbf{B}$ (如果 $\mathbf{A}$ 可逆)
(如果 $\mathbf{A}$ 不可逆，或者为了更数值稳定地计算，通常用级数展开或其他方法计算积分)

而输出方程的离散化通常比较直接：
${\mathbf{C}}_d=\mathbf{C}$
${\mathbf{D}}_d=\mathbf{D}$

这里 $e^{\mathbf{A}{T}_s}$ 是矩阵指数函数，不是每个元素简单求指数！它的计算比较复杂，通常用泰勒级数展开来定义：
$e^{\mathbf{A}{T}_s}=\mathbf{I}+\mathbf{A}{T}_s+\frac{(\mathbf{A}{T}_s{)}^2}{2!}+\frac{(\mathbf{A}{T}_s{)}^3}{3!}+\dots$
其中 $\mathbf{I}$ 是单位矩阵。

好消息是，我们通常不需要手动去计算这些复杂的矩阵指数和积分！ 像MATLAB这样的工程软件提供了非常方便的函数（如 c2d）来自动完成这个离散化过程。我们只需要把连续时间模型的 $\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}$ 矩阵和选定的采样时间 $T_s$ 作为输入，它就能自动帮我们算出 ${\mathbf{A}}_d,{\mathbf{B}}_d,{\mathbf{C}}_d,{\mathbf{D}}_d$。

以我们之前建立的ACC模型为例，离散化过程如下：

1. 写出连续时间模型的矩阵：
   $\mathbf{A}=\left[\begin{array}{ccc}0& 0& 0\\ -1& 0& 1\\ 0& 0& 0\end{array}\right]$,
   $\mathbf{B}=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$,
   ${\mathbf{B}}_w=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$,
   $\mathbf{C}=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\end{array}\right]$,
   $\mathbf{D}=\left[\begin{array}{c}0\\ 0\end{array}\right]$

2. 选择一个合适的采样时间 $T_s$。这个选择很重要：

   • $T_s$ 太大：系统响应慢，控制精度差，可能无法及时应对快速变化（比如前车急刹）。就好比电影帧率太低，你会感觉卡顿。
   • $T_s$ 太小：计算负担重，对执行器的要求高。MPC的计算量本来就比较大，如果 $T_s$ 太小，可能在一个采样周期内完不成一次优化计算。
   • 通常 $T_s$ 的选择需要权衡被控对象的动态特性和控制器的计算能力。对于汽车ACC，常见的采样时间在几十毫秒到几百毫秒之间，比如 $T_s=0.05$秒 (50ms) 或 $T_s=0.1$秒 (100ms)。

3. 调用 c2d 函数 (以MATLAB为例)：
   sys_c = ss(A, [B, Bw], C, D); % 创建连续系统对象，注意B和Bw合并为输入
Ts = 0.1; % 假设选择0.1秒为采样时间
sys_d = c2d(sys_c, Ts, 'zoh'); % 使用ZOH方法进行离散化
Ad = sys_d.A;
Bd_combined = sys_d.B; % 得到的B矩阵会包含原B和Bw对应的列
Bd = Bd_combined(:,1); % 对应原B的离散形式
Bwd = Bd_combined(:,2); % 对应原Bw的离散形式
Cd = sys_d.C;
Dd = sys_d.D;

这样，我们就得到了离散时间的状态空间模型：
$\mathbf{x}(k+1)={\mathbf{A}}_d\mathbf{x}(k)+{\mathbf{B}}_{d}u(k)+{\mathbf{B}}_{wd}w(k)$
$\mathbf{y}(k)={\mathbf{C}}_d\mathbf{x}(k)+{\mathbf{D}}_{d}u(k)$

这个离散模型是MPC控制器进行多步预测的直接依据。MPC会利用这个方程，从当前状态 $\mathbf{x}(k)$ 开始，一步步地迭代预测出 $\mathbf{x}(k+1),\mathbf{x}(k+2),\dots ,\mathbf{x}(k+N_p)$ (其中 $N_p$ 是预测时域的长度)。

为什么离散模型对MPC如此重要？

回顾一下MPC的核心思想：预测未来，滚动优化。

• 预测未来： MPC需要一个模型来告诉它，“如果我施加这样的控制 $u(k),u(k+1),\dots$，那么系统状态 $\mathbf{x}(k+1),\mathbf{x}(k+2),\dots$ 会怎样演变？” 离散状态空间方程 $\mathbf{x}(j+1)={\mathbf{A}}_d\mathbf{x}(j)+{\mathbf{B}}_{d}u(j)$ 正是进行这种一步步迭代预测的完美工具。
• 滚动优化： MPC在每个采样时刻 $k$ 都会进行一次优化计算，这个计算是在离散的时间点上进行的。

所以，一个准确的、与控制器工作方式相匹配的离散模型，是MPC成功应用的关键前提。它就是MPC那双能够“看透”未来几秒钟车辆如何运动的“慧眼”。

今日回顾与展望

今天，我们完成了非常重要的一步——为ACC系统建立了数学模型，并将其转换为了计算机友好的离散形式。我们主要学习了：

1. 车辆纵向动力学基础： 了解了影响汽车前进和后退的主要力，并学会了做合理的简化。
2. 连续时间状态空间模型： 掌握了如何用 $\dot{\mathbf{x}}=\mathbf{Ax}+\mathbf{Bu}$ 和 $\mathbf{y}=\mathbf{Cx}+\mathbf{Du}$ 来描述ACC中本车速度、相对距离、前车速度这“三驾马车”的动态关系，并推导出了具体的A, B, C, D矩阵。
3. 模型离散化： 理解了为什么需要将连续模型转化为离散模型，了解了零阶保持器（ZOH）的基本思想，以及如何通过工具（如MATLAB的 c2d）得到离散模型的 ${\mathbf{A}}_d,{\mathbf{B}}_d,{\mathbf{C}}_d,{\mathbf{D}}_d$ 矩阵。

这个离散的状态空间模型，就是我们下一讲设计MPC控制器的“原材料”。有了它，MPC才能开始它的“预测”和“优化”表演。

在明天的博客中，我们将正式进入MPC控制器的设计环节，探讨MPC是如何利用今天建立的模型，来定义优化目标、处理各种约束，并最终计算出最优的控制指令的。那将是MPC核心魅力的展现，敬请期待！

习题

又到了检验学习成果的时候啦！下面几道题，帮你巩固今天的内容。

1. 思考题：在ACC的“三驾马车”状态空间模型中，我们将本车期望加速度 $a_{ego}$ 作为控制输入 $u(t)$，而不是直接将油门开度或刹车压力作为输入。这样做有什么好处和潜在的简化假设？

2. 填空题：在状态空间方程 $\dot{\mathbf{x}}(t)=\mathbf{Ax}(t)+\mathbf{B}u(t)$ 中，矩阵 $\mathbf{A}$ 描述了系统的 ______ 特性，矩阵 $\mathbf{B}$ 描述了 ______ 如何影响状态的变化。

3. 简答题：为什么在数字计算机上实现控制算法时，通常需要将连续时间系统模型进行离散化？离散化过程中，采样时间 $T_s$ 的选择对系统有什么影响？

4. (选做，概念理解) 如果我们有一个非常简单的连续系统 $\dot{x}(t)=-2x(t)+u(t)$，并且使用前向欧拉法进行离散化，其离散化公式为 $x(k+1)=x(k)+T_s\cdot \dot{x}(k)$。请写出使用前向欧拉法得到的离散状态方程 $x(k+1)=A_{d}x(k)+B_{d}u(k)$ 中的 $A_d$ 和 $B_d$ 是什么（用 $T_s$ 表示）？ (提示: 将 $\dot{x}(k)$ 的表达式代入)

---

答案：

1. 答案：

   • 好处：
     1. 简化上层控制器设计： 将复杂的发动机油门控制、刹车液压控制等底层执行器动态解耦，使得ACC的MPC控制器可以专注于更高层级的纵向运动规划和控制（即决定需要多大的加速度），而不需要关心如何具体实现这个加速度。
     2. 模块化： 底层执行器控制可以作为一个独立的模块进行设计和标定，上层ACC控制器则更具通用性。
     3. 更直接的物理意义： 加速度是描述运动变化的核心物理量，直接以加速度为控制输入，更符合运动学和动力学的直观理解。
   • 潜在的简化假设：
     1. 底层控制器性能理想： 假设存在一个响应足够快、精度足够高的底层控制器，能够完美地、无延迟地跟踪上层MPC给出的期望加速度指令 $a_{ego}$。
     2. 忽略执行器饱和和动态： 假设期望的加速度总是在车辆实际能够提供的能力范围内，并且不考虑从指令发出到实际加速度产生之间的延迟和动态过程。在实际MPC设计中，执行器的饱和限制（最大/最小加速度）通常会作为约束条件加入到优化问题中。

2. 答案：
   矩阵 $\mathbf{A}$ 描述了系统的 内部动态（或自由响应） 特性（即在没有外部输入的情况下，状态如何自己演化）。
   矩阵 $\mathbf{B}$ 描述了 控制输入 如何影响状态的变化。

3. 答案：

   • 为什么需要离散化： 数字计算机本质上是按离散的时钟节拍工作的，它们通过采样来获取连续信号的值，并在离散的时间点上进行计算和输出控制指令。连续模型描述的是变量在无限小时间间隔内的变化，这不符合计算机的运算模式。离散化将连续的微分方程转换为差分方程，使得计算机可以在每个采样周期进行迭代计算。
   • 采样时间 $T_s$ 的影响：
     • $T_s$ 过大：
       • 系统对变化的响应滞后，控制精度下降。
       • 可能无法捕捉到系统中一些快速的动态特性，甚至导致系统不稳定（如果采样频率低于奈奎斯特频率的两倍）。
       • 对于MPC，预测的准确性会降低，因为在一个较长的采样周期内，系统状态和扰动可能发生较大变化，而ZOH假设控制输入在此期间不变。
     • $T_s$ 过小：
       • 增加了计算机的计算负担，因为单位时间内需要进行更多的计算。对于计算量较大的MPC算法，可能会导致在一个采样周期内无法完成优化计算。
       • 对硬件（传感器、执行器）的响应速度要求更高。
       • 可能会引入不必要的噪声敏感性。
         因此，采样时间 $T_s$ 的选择是一个权衡，需要根据被控对象的动态特性、期望的闭环性能以及控制器的计算能力来综合决定。

4. 答案：
   连续系统为： $\dot{x}(t)=-2x(t)+u(t)$
   前向欧拉离散化公式： $x(k+1)=x(k)+T_s\cdot \dot{x}(k)$
   将 $\dot{x}(k)=-2x(k)+u(k)$ 代入上述欧拉公式：
   $x(k+1)=x(k)+T_s\cdot (-2x(k)+u(k))$
   $x(k+1)=x(k)-2T_{s}x(k)+T_{s}u(k)$
   整理得到：
   $x(k+1)=(1-2T_s)x(k)+T_{s}u(k)$
   与标准离散状态方程 $x(k+1)=A_{d}x(k)+B_{d}u(k)$ 对比，可得：
   $A_d=(1-2T_s)$
   $B_d=T_s$