当前位置：首页 > news >正文

6.13.拓扑排序

news 来源：原创 2025/5/23 10:35:15

一.AOV网：

以上述图片为例，上述图片里的图是一个有向无环图（DAG图），其中顶点表示活动，有向边<Vi,Vj>表示活动Vi必须先于活动Vj进行，比如"洗番茄"之前要先"买菜"，"洗番茄"之后才可以"切番茄"，但除了有番茄之外，还需要"准备厨具"，因此"准备厨具"且"洗番茄"之后才开始"切番茄"。

注：AOV网一定是一个有向无环图，如果图中存在环路，那么就不是AOV网，如下图->

如上图，"洗番茄"和"切番茄"之间产生了环路。

二.拓扑排序：

1.定义：

2.实例：

如上图，拓扑排序放到AOV网中，其实就是要求找到做事的先后顺序。

如上图，要做番茄炒蛋，这一个流程其实可以从"准备厨具"和"买菜"作为起点，此时先"准备厨具"，如下图：

如上图，"准备厨具"后就需要"买菜"，不可能先"打鸡蛋"或"洗番茄"，因为此时还没有菜，因此接下来要做的是"买菜"，如下图：

如上图，此时可以选择先"打鸡蛋"或"洗番茄"，此次选择"洗番茄"，如下图：

如上图，再往后可以选择"打鸡蛋"或者"切番茄"，此次选择"切番茄"，如下图：

如上图，现在番茄准备好了，就必须"打鸡蛋"，要不然无法"下锅炒"，因此该"打鸡蛋"，如下图：

如上图，此时该"下锅炒"，如下图：

如上图，最后就该"吃"了，如下图：

如上图，可以按照以上的顺序来依次地完成番茄炒蛋这个流程中的每一个步骤，刚才对番茄炒蛋的AOV网进行了拓扑排序，整个过程可以总结为上述图片里的步骤：

步骤一：每次从AOV网中选择一个没有前驱（入度为0）的顶点并输出，之所以把这个顶点先输出，是因为一个顶点的入度为0，就意味着这个顶点所表示的活动在它之前不需要任何的准备活动；

步骤二：从AOV网中删除步骤一中操作的顶点和所有以该顶点为起点的有向边；

步骤三：不断重复步骤一和步骤二，直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。

3.总结：

结合刚才的例子，拓扑排序的定义会更好理解，从刚才进行拓扑排序的过程可以得知，每一个AOV网有可能有一个或者多个拓扑排序序列，比如上述图片中的AOV网可以以"准备厨具"为起点，也可以以"买菜"为起点->起点的不同，导致最终拓扑排序的序列不同。

4.细节及拓扑排序的实现步骤：

注：不是所有的图都可以进行拓扑排序，只要图中存在回路，那这个图就不能拓扑排序。

举例如下图：

如上图，本次以"准备厨具"为起点，如下图：

如上图，接下来"买菜"，如下图：

如上图，接下来只能选择"打鸡蛋"，因为只有"打鸡蛋"这个顶点的入度为0，如下图：

如上图，此时图中所有顶点的入度都大于0（即存在前驱），在这种情况下就没办法按照刚才的规则继续删除顶点，

所以如果图中存在回路，那这样的图就不能进行拓扑排序，如果原图是DAG图即有向无环图，那这种图就能够进行拓扑排序。

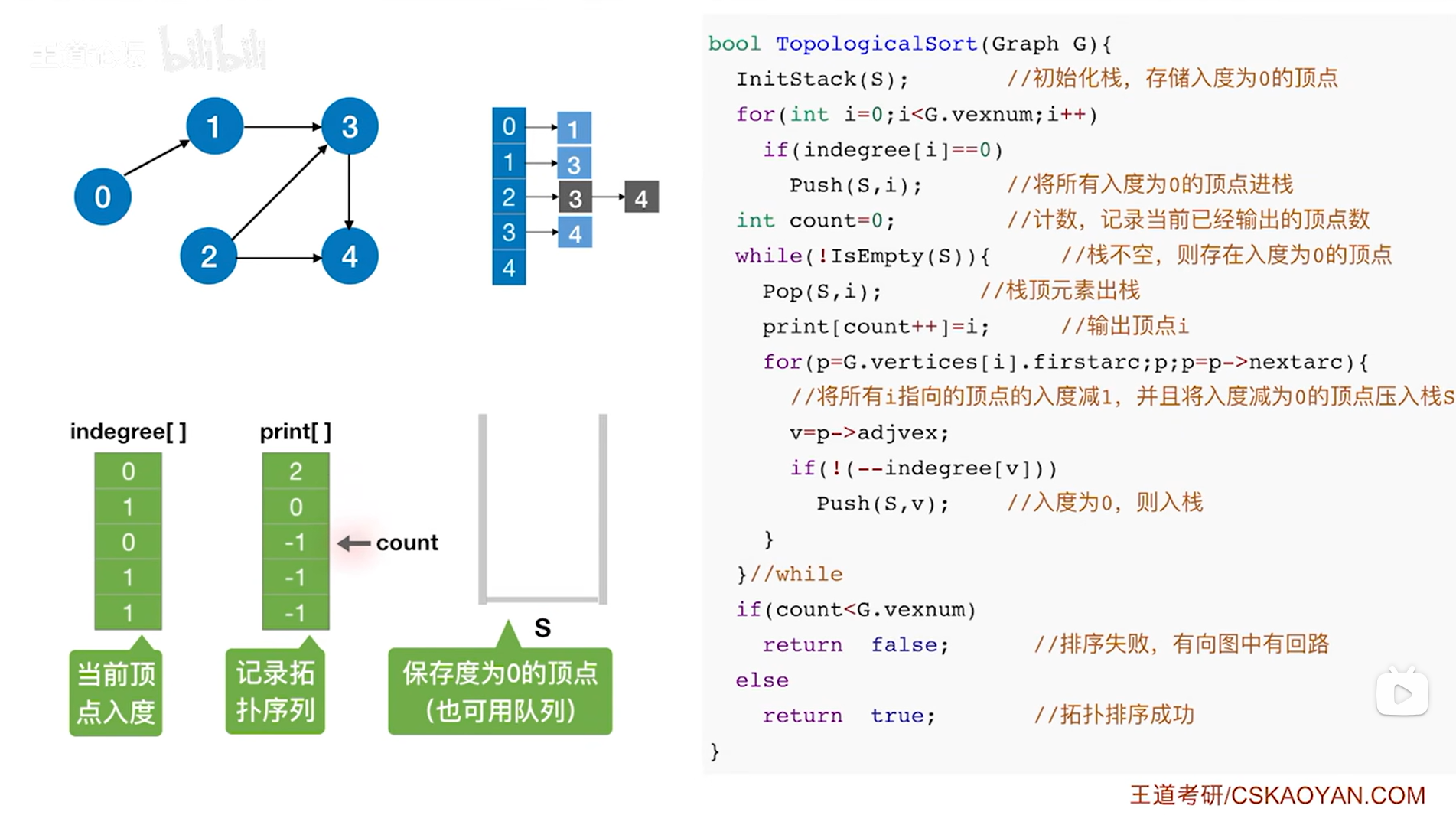
三.拓扑排序代码实现：

1.代码：

对上述图片中的代码解读：

上述图片左侧的代码是基于图的邻接表的存储方式进行的，详情见"6.3.图的存储结构-邻接表法"
该代码中省略了indegree数组和print数组的定义，写代码时要自己加上，其中indegree数组用于记录每一个顶点当前的入度，print数组用于记录得到的拓扑排序序列，如下图：

如上图，其中还需要定义一个栈，用栈来保存当前度为0的顶点，当然这个栈也可以用队列或者数组来代替
InitStack(S)即初始化栈、Push(S,i)即入栈操作、isEmpty(S)判断栈是否为空、Pop(S,i)即出栈操作详情见"3.2.栈的顺序存储实现"

2.实例：

以上述图片的有向图为例，首先需要初始图（用邻接表存储）、indegree数组（记录图中各个顶点当前的入度）、print数组（记录拓扑排序序列）、栈S（保存入度为0的顶点）->

通过定义图来把该有向图表示出来，且用邻接表存储该图；

0号顶点的入度为0->indegree数组的0索引为0，

1号顶点的入度为1（因为有且只有0号顶点指向1号顶点）->indegree数组的1索引为1，

2号顶点的入度为0->indegree数组的2索引为0，

3号顶点的入度为2->indegree数组的3索引为2，

4号顶点的入度为2->indegree数组的4索引为2；

print数组初始化时会把里面的所有数据初始化为-1，表示拓扑排序序列还没有完成；

TopologicalSort函数的返回值是bool型，形参是图G，本例是上述图片的有向图，

首先执行InitStack(S)即初始化栈，用于存储入度为0的顶点，如下图：

如上图，

第一个for循环用于把当前所有入度为0的顶点压入栈S（G.vexnum表示图中当前的顶点数，indegree数组由图G确定，所以indegree数组的索引和图G的索引一一对应），

通过indegree数组可以确定当前入度为0的顶点有0号顶点和2号顶点，所以调用Push(S,i)使这两个顶点压入栈S，至此第一个for循环结束，

(对一个图进行拓扑排序的过程，其实就是不断地删除当前入度为0的顶点，目前来看入度为0的顶点已经全部压入栈S，所以接下来可以通过栈S里保存的顶点来确定拓扑排序序列当中第一个顶点)

继续定义了一个变量count，初始值为0，count用于记录当前已经完成拓扑排序的顶点的个数，初始时所有顶点都没有进行拓扑排序，所以为0，

如下图：

如上图，

接下来要判断while循环是否执行，此时栈S不为空，因此isEmpty(S)为false，所以!isEmpty(S)为true，因此执行本层while循环，首先执行Pop(S,i)把栈顶元素i即2号顶点弹出栈（此时i索引上的顶点是当前图中最后一个会入栈的顶点即2号顶点，因此在栈顶，通过调用Pop(S,i)函数可以把i赋值为此时的栈顶元素即2号顶点，同时栈的长度减1，详情见"3.2.栈的顺序存储实现"），

首先把print数组0索引上的数据赋值为此时的栈顶元素即2号顶点，表示拓扑排序序列中第一个元素为2号顶点，然后count++即count为1，表示已经输出了1个顶点（注意：print[count++]=i是先执行print[count]=i，再count++），

接下来执行while循环里的for循环，此时G.vertices[i]表示图G中2号顶点，G.vertices[i].firstarc即p表示图G中2号顶点指向的第一条弧即2号顶点指向3号顶点的弧，只要p不为NULL，该for循环就执行，此时p不为NULL，因此执行for循环，p->adjvex表示p表示的弧指向的顶点，此时指向3号顶点，因此p->adjvex的值v为3，

继续while循环里的for循环的if语句，由于此时逻辑上删除了2号顶点，所以v代表的3号顶点的入度减1即--indegree[v]，此时3号顶点的入度为1，如果--indegree[v]为0即v号顶点的入度减1后变为0，那么就执行该if语句实现把v号顶点入栈，显然此时3号顶点的入度不为0，因此不执行if语句，本层for循环结束，

执行p=p->nextarc后可知p此时表示2号顶点指向4号顶点的弧（因为2号顶点指向的第二条弧即2号顶点指向4号顶点的弧），同理p->adjvex的值v为4，执行--indegree[v]后可知4号顶点的入度为1，显然不执行该if语句，本层for循环结束，

执行p=p->nextarc后可知p此时为NULL（因为2号顶点只有2号顶点指向3号顶点的弧和2号顶点指向4号顶点的弧），for循环结束，

所以本层while循环结束，

（注:操作中只是逻辑上把2号顶点还有与2号顶点相连的弧都删除了，但图中邻接表上的2号顶点是没有改变的）

如下图：

如上图，

接下来要判断while循环是否执行，此时栈S不为空，因此isEmpty(S)为false，所以!isEmpty(S)为true，因此执行本层while循环，首先执行Pop(S,i)把栈顶元素i即0号顶点弹出栈（此时i索引上的顶点是2号顶点，通过调用Pop(S,i)函数可以把i赋值为此时的栈顶元素即0号顶点，同时栈的长度减1，详情见"3.2.栈的顺序存储实现"），

首先把print数组1索引上的数据赋值为此时的栈顶元素即0号顶点，表示拓扑排序序列中第二个元素为0号顶点，然后count++即count为2，表示已经输出了2个顶点（注意：print[count++]=i是先执行print[count]=i，再count++），

接下来执行while循环里的for循环，此时G.vertices[i]表示图G中0号顶点，G.vertices[i].firstarc即p表示图G中0号顶点指向的第一条弧即0号顶点指向1号顶点的弧，只要p不为NULL，该for循环就执行，此时p不为NULL，因此执行for循环，p->adjvex表示p表示的弧指向的顶点，此时指向1号顶点，因此p->adjvex的值v为1，

继续while循环里的for循环的if语句，由于此时逻辑上删除了0号顶点，所以v代表的1号顶点的入度减1即--indegree[v]，此时1号顶点的入度为0，如果--indegree[v]为0即v号顶点的入度减1后变为0，那么就执行该if语句实现把v号顶点入栈，显然此时1号顶点的入度为0，因此执行if语句把1号顶点压入栈S，本层for循环结束，

执行p=p->nextarc后可知p此时为NULL（因为0号顶点只有0号顶点指向1号顶点这一条弧），for循环结束，

所以本层while循环结束，

（注:操作中只是逻辑上把0号顶点还有与0号顶点相连的弧都删除了，但图中邻接表上的0号顶点是没有改变的）

如下图：

如上图，

接下来要判断while循环是否执行，此时栈S不为空，因此isEmpty(S)为false，所以!isEmpty(S)为true，因此执行本层while循环，首先执行Pop(S,i)把栈顶元素i即1号顶点弹出栈（此时i索引上的顶点是0号顶点，通过调用Pop(S,i)函数可以把i赋值为此时的栈顶元素即1号顶点，同时栈的长度减1，详情见"3.2.栈的顺序存储实现"），

首先把print数组2索引上的数据赋值为此时的栈顶元素即1号顶点，表示拓扑排序序列中第三个元素为1号顶点，然后count++即count为3，表示已经输出了3个顶点（注意：print[count++]=i是先执行print[count]=i，再count++），

接下来执行while循环里的for循环，此时G.vertices[i]表示图G中1号顶点，G.vertices[i].firstarc即p表示图G中1号顶点指向的第一条弧即1号顶点指向3号顶点的弧，只要p不为NULL，该for循环就执行，此时p不为NULL，因此执行for循环，p->adjvex表示p表示的弧指向的顶点，此时指向3号顶点，因此p->adjvex的值v为3，

继续while循环里的for循环的if语句，由于此时逻辑上删除了1号顶点，所以v代表的3号顶点的入度减1即--indegree[v]，此时3号顶点的入度为0，如果--indegree[v]为0即v号顶点的入度减1后变为0，那么就执行该if语句实现把v号顶点入栈，显然此时3号顶点的入度为0，因此执行if语句把3号顶点压入栈S，本层for循环结束，

执行p=p->nextarc后可知p此时为NULL（因为1号顶点只有1号顶点指向3号顶点这一条弧），for循环结束，

所以本层while循环结束，

（注:操作中只是逻辑上把1号顶点还有与1号顶点相连的弧都删除了，但图中邻接表上的1号顶点是没有改变的）

如下图：

如上图，

接下来要判断while循环是否执行，此时栈S不为空，因此isEmpty(S)为false，所以!isEmpty(S)为true，因此执行本层while循环，首先执行Pop(S,i)把栈顶元素i即3号顶点弹出栈（此时i索引上的顶点是1号顶点，通过调用Pop(S,i)函数可以把i赋值为此时的栈顶元素即3号顶点，同时栈的长度减1，详情见"3.2.栈的顺序存储实现"），

首先把print数组3索引上的数据赋值为此时的栈顶元素即3号顶点，表示拓扑排序序列中第四个元素为3号顶点，然后count++即count为4，表示已经输出了4个顶点（注意：print[count++]=i是先执行print[count]=i，再count++），

接下来执行while循环里的for循环，此时G.vertices[i]表示图G中3号顶点，G.vertices[i].firstarc即p表示图G中3号顶点指向的第一条弧即3号顶点指向4号顶点的弧，只要p不为NULL，该for循环就执行，此时p不为NULL，因此执行for循环，p->adjvex表示p表示的弧指向的顶点，此时指向4号顶点，因此p->adjvex的值v为4，

继续while循环里的for循环的if语句，由于此时逻辑上删除了3号顶点，所以v代表的4号顶点的入度减1即--indegree[v]，此时4号顶点的入度为0，如果--indegree[v]为0即v号顶点的入度减1后变为0，那么就执行该if语句实现把v号顶点入栈，显然此时4号顶点的入度为0，因此执行if语句把4号顶点压入栈S，本层for循环结束，

执行p=p->nextarc后可知p此时为NULL（因为3号顶点只有3号顶点指向4号顶点这一条弧），for循环结束，

所以本层while循环结束，

（注:操作中只是逻辑上把3号顶点还有与3号顶点相连的弧都删除了，但图中邻接表上的3号顶点是没有改变的）

如下图：

如上图，

接下来要判断while循环是否执行，此时栈S不为空，因此isEmpty(S)为false，所以!isEmpty(S)为true，因此执行本层while循环，首先执行Pop(S,i)把栈顶元素i即4号顶点弹出栈（此时i索引上的顶点是3号顶点，通过调用Pop(S,i)函数可以把i赋值为此时的栈顶元素即4号顶点，同时栈的长度减1，详情见"3.2.栈的顺序存储实现"），

首先把print数组4索引上的数据赋值为此时的栈顶元素即4号顶点，表示拓扑排序序列中第五个元素为4号顶点，然后count++即count为5，表示已经输出了5个顶点（注意：print[count++]=i是先执行print[count]=i，再count++），

接下来执行while循环里的for循环，此时G.vertices[i]表示图G中4号顶点，G.vertices[i].firstarc即p表示图G中4号顶点指向的第一条弧，显然4号顶点不指向任何一条弧，因此p为NULL，只要p不为NULL，该for循环就执行，此时p为NULL，因此不执行for循环，for循环结束，

所以本层while循环结束，

（注:操作中只是逻辑上把4号顶点删除了，但图中邻接表上的4号顶点是没有改变的）

如下图：

如上图，

接下来要判断while循环是否执行，此时栈S为空，因此isEmpty(S)为true，所以!isEmpty(S)为false，最终整个while循环结束，

继续要判断TopologicalSort函数中最后一个if-else语句如何执行，如果count<G.vexnum即输出的顶点个数小于图中顶点个数时执行if语句，返回false，表示排序失败，因为输出的顶点个数小于图中顶点个数只可能是图中存在回路，存在回路的图无法进行拓扑排序，

除此之外表示拓扑排序成功，返回true，

此时count的值等于5，等于图中顶点的数量，这就表示拓扑排序是成功的，返回true。

3.代码的效率分析：

如上图，假设图中共有V个顶点，E条边，

如果该图采用邻接表存储，该图实现拓扑排序的代码如上图，可知拓扑排序的过程中每一个顶点都会入栈处理一次，图中的每一条弧也都需要遍历一次，所以整体来看时间复杂度为O( |V| + |E| )；

如果该图采用邻接矩阵存储，遍历完所有的顶点和弧其实就是扫描完整个图的邻接矩阵，所以整体来看时间复杂度为O( |V| * |V| )。

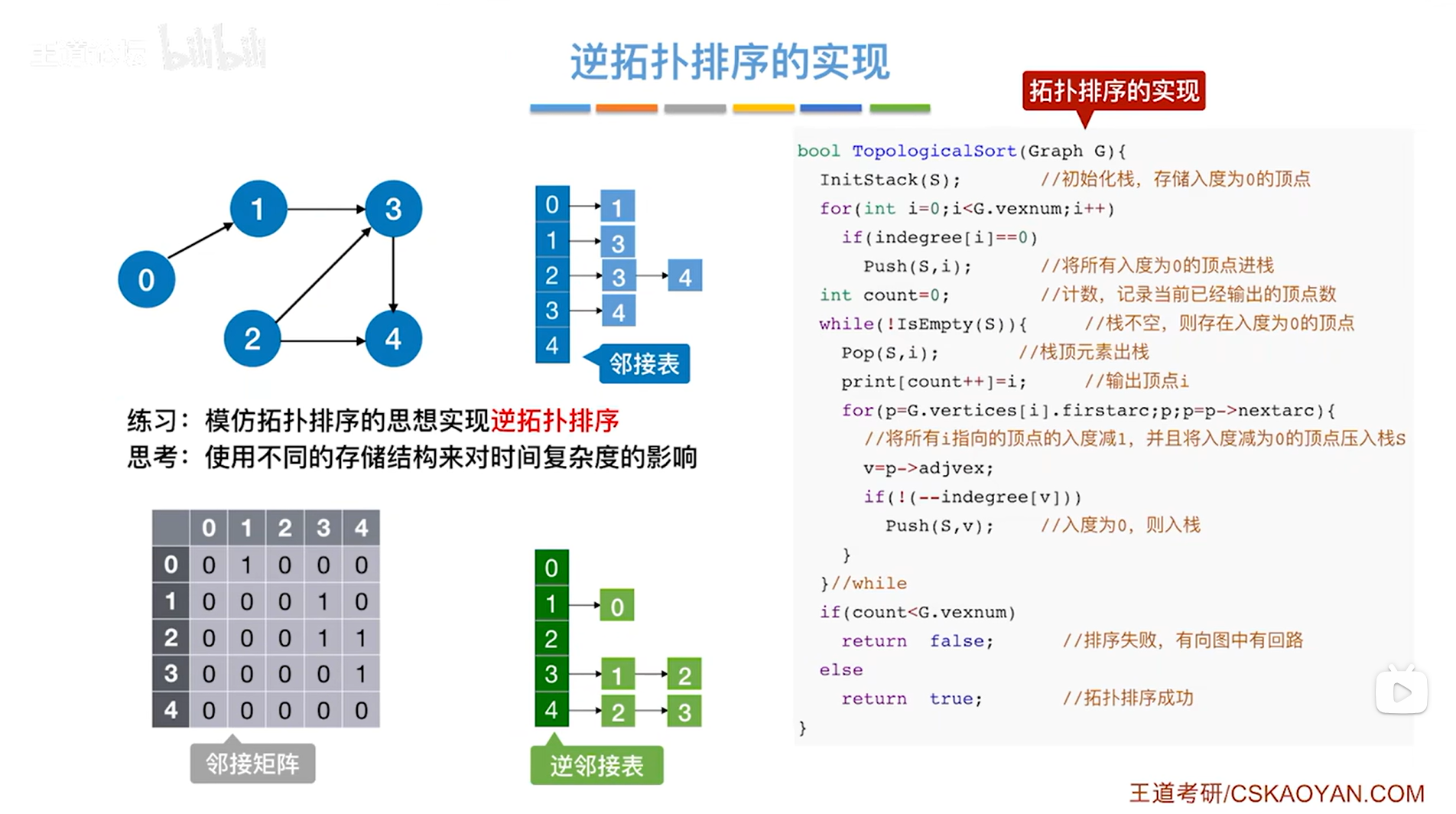
四.逆拓扑排序：

1.逆拓扑排序的实现步骤：

如上图，逆拓扑排序类似拓扑排序，只不过每一次选择的是删除图中出度为0的顶点。

2.实例：

以上述图片的有向无环图为例，可知只有"吃"的出度为0，所以删除"吃"和所有以"吃"为终点的有向边，如下图：

如上图，可知只有"下锅炒"的出度为0，所以删除"下锅炒"和所有以"下锅炒"为终点的有向边，如下图：

如上图，可知"打鸡蛋"和"切番茄"的出度都为0，所以"打鸡蛋"和"切番茄"可以任选一个删除，本例中删除"切番茄"和所有以"切番茄"为终点的有向边，如下图：

如上图，可知"打鸡蛋"和"洗番茄"的出度都为0，所以"打鸡蛋"和"洗番茄"可以任选一个删除，本例中删除"洗番茄""和所有以"洗番茄"为终点的有向边，如下图：

如上图，可知只有"打鸡蛋"的出度为0，所以删除"打鸡蛋"和所有以"打鸡蛋"为终点的有向边，如下图：

如上图，可知"准备厨具"和"买菜"的出度都为0，所以"准备厨具"和"买菜"可以任选一个删除，本例中删除"准备厨具"和所有以"准备厨具"为终点的有向边，同理，最后删除"买菜"和所有以"买菜"为终点的有向边，如下图：

至此，完成了该逆拓扑排序。

3.代码实现：

逆拓扑排序的代码实现与拓扑排序的代码实现的思路一样，

只不过拓扑排序关注的是顶点的入度，逆拓扑排序关注的是顶点的出度，

逆拓扑排序的代码实现自行思考。

4.效率：

图采用不同的存储结构，那么对于代码的时间复杂度的影响是很大的，

因为在逆拓扑排序中如果删除了一个顶点，同时也需要删除所有以该顶点为终点的有向边->

如果图采用邻接表存储的话，如果删除一个顶点后，要找到指向该顶点的所有边，需要把整个邻接表都遍历一遍才能找全，所以采用邻接表来实现图的逆拓扑排序是比较低效的；

如果图采用邻接矩阵的话，如果删除一个顶点后，要找到指向该顶点的所有边，只需要遍历该顶点在邻接矩阵中对应的那一列（竖着的，如上述图片中邻接矩阵里红圈标注的4号顶点以及4号顶点下的箭头），所以采用邻接矩阵来实现图的逆拓扑排序是比较高效的。

5.逆邻接表：

如上图，

在邻接表中，每一个顶点所对应的链表保存的是从该顶点出发，直接所指向的顶点，比如上述图片中2号顶点对应的链表中有3、4，表示从2号顶点出发直接指向3号顶点和4号顶点；

而在逆邻接表中，每一个顶点所对应的链表保存的是直接以该顶点为终点，哪些顶点是起点，比如上述图片中3号顶点对应的链表中有1、2，表示直接以3号顶点为终点的顶点有1号顶点和2号顶点；

所以在逆邻接表中，找到有哪些顶点是直接指向当前的顶点是很方便的。

（注：逆邻接表的代码实现与邻接表的类似，只不过存储的数据不同，如上图的例子）

五.逆拓扑排序的实现-DFS算法（深度优先算法）：

1.复习：DFS算法

如上图，是DFS算法的完整代码，详情见"6.7.图的深度优先遍历(英文缩写DFS)"，

在DFS函数中，调用visit(v)函数访问v号顶点后，需要把这个顶点对应的visited值修改为true，

现在使用DFS算法实现逆拓扑排序，只需要做稍微的改动即可，如下->

2.使用DFS算法完成逆拓扑排序的代码实现：

DFSTraverse函数不变，DFS函数上需做改动，执行visited[v]=true表示v号顶点已被访问，并且执行完for循环即访问完与v号顶点相邻接的所有顶点之后，会调用print函数把v号顶点输出出来，使用这种方式输出得到的序列就是逆拓扑排序序列。

3.实例：

以上述图片的DAG图为例，

DFSTraverse函数的形参Graph G是图，返回值为void，调用DFSTraverse函数，

首先执行第一个for循环，v初始为0，当v小于G.vexnum时执行for循环，G.vexnum表示图中当前的顶点数即5，因此会执行for循环，执行visited[v]=false把图中所有顶点的visited值赋值为false，表示图中所有顶点都还没有被访问过，

继续执行第二个for循环，v初始为0，当v小于G.vexnum时执行for循环，G.vexnum表示图中当前的顶点数即5，因此会执行for循环，如果v号顶点没有被访问过即visited[v]为false，!visited[v]为true，那么就执行if语句并调用DFS函数，传入图G和v号顶点->此时0号顶点还没有被访问过，即visited[0]=false，所以!visited[0]为true，因此执行if语句调用DFS函数，传入图G和0号顶点即v为0（0号顶点入递归栈，DFS算法相当于使用栈），如下图：

如上图，调用DFS函数，传入的是图G和0号顶点即v为0，

首先执行visited[v]=true把0号顶点的visited值赋值为true，表示0号顶点已经被访问过（在上述图里，如果把某个顶点标为灰色，意味着该顶点的visited值为true即该顶点已经被访问过），

接下来执行for循环，执行w=FirstNeighbor(G,v)表示在图G中找到v号顶点指向的第一个顶点->此时0号顶点指向的第一个顶点是1号顶点即w为1，w为1即符合循环条件w>=0，因此执行本层for循环，

继续判断是否执行if语句，如果w号顶点没有被访问过即visited[w]为false，!visited[w]为true，那么就执行if语句并调用DFS函数，传入图G和w号顶点->此时1号顶点还没有被访问即visited[1]为false，所以!visited[1]为true，因此执行if语句调用DFS函数，传入图G和1号顶点，如下图：

如上图，调用DFS函数，传入的是图G和1号顶点即v为1，

首先执行visited[v]=true把1号顶点的visited值赋值为true，表示1号顶点已经被访问过（在上述图里，如果把某个顶点标为灰色，意味着该顶点的visited值为true即该顶点已经被访问过），

接下来执行for循环，执行w=FirstNeighbor(G,v)表示在图G中找到v号顶点指向的第一个顶点->此时1号顶点指向的第一个顶点是3号顶点即w为3，w为3即符合循环条件w>=0，因此执行本层for循环，

继续判断是否执行if语句，如果w号顶点没有被访问过即visited[w]为false，!visited[w]为true，那么就执行if语句并调用DFS函数，传入图G和w号顶点->此时3号顶点还没有被访问即visited[3]为false，所以!visited[3]为true，因此执行if语句调用DFS函数，传入图G和3号顶点，如下图：

如上图，调用DFS函数，传入的是图G和3号顶点即v为3，

首先执行visited[v]=true把3号顶点的visited值赋值为true，表示3号顶点已经被访问过（在上述图里，如果把某个顶点标为灰色，意味着该顶点的visited值为true即该顶点已经被访问过），

接下来执行for循环，执行w=FirstNeighbor(G,v)表示在图G中找到v号顶点指向的第一个顶点->此时3号顶点指向的第一个顶点是4号顶点即w为4，w为4即符合循环条件w>=0，因此执行本层for循环，

继续判断是否执行if语句，如果w号顶点没有被访问过即visited[w]为false，!visited[w]为true，那么就执行if语句并调用DFS函数，传入图G和w号顶点->此时4号顶点还没有被访问即visited[4]为false，所以!visited[4]为true，因此执行if语句调用DFS函数，传入图G和4号顶点，如下图：

如上图，调用DFS函数，传入的是图G和4号顶点即v为4，

首先执行visited[v]=true把4号顶点的visited值赋值为true，表示4号顶点已经被访问过（在上述图里，如果把某个顶点标为灰色，意味着该顶点的visited值为true即该顶点已经被访问过），

接下来执行for循环，执行w=FirstNeighbor(G,v)表示在图G中找到v号顶点指向的第一个顶点->此时4号顶点不指向任何一个顶点即w小于0，w小于0不符合循环条件w>=0，因此不执行for循环，

最后就会调用print(v)函数把v号顶点输出->此时把4号顶点输出->所以得到的逆拓扑排序序列中第一个顶点是4号顶点，

至此，关于4号顶点的DFS函数执行完毕（4号顶点弹出递归栈），需要返回到上一层的DFS函数调用即传入图G和3号顶点的DFS函数，

如下图：

如上图，返回到传入图G和3号顶点即v为3的DFS函数，此时w为4（因为传入图G和4号顶点即v为4的那一层DFS函数里的w的值是局部变量，当传入图G和4号顶点即v为4的那一层DFS函数结束后就不存在了，到了传入图G和3号顶点即v为3的DFS函数中w就是当时传入图G和3号顶点即v为3的DFS函数时得出的w的值即4），

接下来继续执行for循环，执行w=NextNeighor(G,v,w)表示在图G中找到除w号顶点之外v号顶点指向的下一个顶点（详情见"6.5.图的基本操作"）->在图G中找除4号顶点之外3号顶点指向的下一个顶点显然找不到，因为3号顶点只指向4号顶点这一个顶点，因此w小于0，w小于0不符合循环条件w>=0，因此不执行for循环，

最后就会调用print(v)函数把v号顶点输出->此时把3号顶点输出->所以得到的逆拓扑排序序列中第二个顶点是3号顶点，

至此，关于3号顶点的DFS函数执行完毕（3号顶点弹出递归栈），需要返回到上一层的DFS函数调用即传入图G和1号顶点的DFS函数，

如下图：

如上图，返回到传入图G和1号顶点即v为1的DFS函数，此时w为3（因为传入图G和3号顶点即v为3的那一层DFS函数里的w的值是局部变量，当传入图G和3号顶点即v为3的那一层DFS函数结束后就不存在了，到了传入图G和1号顶点即v为1的DFS函数中w就是当时传入图G和1号顶点即v为1的DFS函数时得出的w的值即3），

接下来继续执行for循环，执行w=NextNeighor(G,v,w)表示在图G中找到除w号顶点之外v号顶点指向的下一个顶点（详情见"6.5.图的基本操作"）->在图G中找除3号顶点之外1号顶点指向的下一个顶点显然找不到，因为1号顶点只指向3号顶点这一个顶点，因此w小于0，w小于0不符合循环条件w>=0，因此不执行for循环，

最后就会调用print(v)函数把v号顶点输出->此时把1号顶点输出->所以得到的逆拓扑排序序列中第三个顶点是1号顶点，

至此，关于1号顶点的DFS函数执行完毕（1号顶点弹出递归栈），需要返回到上一层的DFS函数调用即传入图G和0号顶点的DFS函数，

如下图：

如上图，返回到传入图G和0号顶点即v为0的DFS函数，此时w为1（因为传入图G和1号顶点即v为1的那一层DFS函数里的w的值是局部变量，当传入图G和1号顶点即v为1的那一层DFS函数结束后就不存在了，到了传入图G和0号顶点即v为0的DFS函数中w就是当时传入图G和0号顶点即v为0的DFS函数时得出的w的值即1），

接下来继续执行for循环，执行w=NextNeighor(G,v,w)表示在图G中找到除w号顶点之外v号顶点指向的下一个顶点（详情见"6.5.图的基本操作"）->在图G中找除1号顶点之外0号顶点指向的下一个顶点显然找不到，因为0号顶点只指向1号顶点这一个顶点，因此w小于0，w小于0不符合循环条件w>=0，因此不执行for循环，

最后就会调用print(v)函数把v号顶点输出->此时把0号顶点输出->所以得到的逆拓扑排序序列中第四个顶点是0号顶点，

至此，关于0号顶点的DFS函数执行完毕（0号顶点弹出递归栈），

如下图：

如上图，

现在就回到了DFSTraverse函数中的第二个for循环内，此时0号顶点和有关于0号顶点的操作全部结束，会继续往后遍历，

如果v号顶点没有被访问过即visited[v]为false，!visited[v]为true，那么就执行if语句并调用DFS函数，传入图G和v号顶点->（注：在上述图里，如果把某个顶点标为灰色，意味着该顶点的visited值为true即该顶点已经被访问过）此时2号顶点还没有被访问过，即visited[2]=false，所以!visited[2]为true，因此执行if语句调用DFS函数，传入图G和2号顶点即v为2（2号顶点入递归栈，DFS算法相当于使用栈），

如下图：

如上图，调用DFS函数，传入的是图G和2号顶点即v为2，

首先执行visited[v]=true把2号顶点的visited值赋值为true，表示2号顶点已经被访问过（在上述图里，如果把某个顶点标为灰色，意味着该顶点的visited值为true即该顶点已经被访问过），

接下来执行for循环，执行w=FirstNeighbor(G,v)表示在图G中找到v号顶点指向的第一个顶点->此时2号顶点指向的第一个顶点是3号顶点即w为3，w为3即符合循环条件w>=0，因此执行本层for循环，

继续判断是否执行if语句，如果w号顶点没有被访问过即visited[w]为false，!visited[w]为true，那么就执行if语句并调用DFS函数，传入图G和w号顶点->此时3号顶点已经被访问即visited[3]为true，所以!visited[1]为false，因此不执行if语句，本层for循环结束，

接下来继续执行for循环，执行w=NextNeighor(G,v,w)表示在图G中找到除w号顶点之外v号顶点指向的下一个顶点（详情见"6.5.图的基本操作"）->在图G中找除3号顶点之外2号顶点指向的下一个顶点是4号顶点即w为4，w为4即符合循环条件w>=0，因此执行本层for循环，

继续判断是否执行if语句，如果w号顶点没有被访问过即visited[w]为false，!visited[w]为true，那么就执行if语句并调用DFS函数，传入图G和w号顶点->此时4号顶点已经被访问即visited[4]为true，所以!visited[4]为false，因此不执行if语句，本层for循环结束，

接下来继续执行for循环，执行w=NextNeighor(G,v,w)表示在图G中找到除w号顶点之外v号顶点指向的下一个顶点（详情见"6.5.图的基本操作"）->在图G中找除4号顶点之外2号顶点指向的下一个顶点显然找不到，因为2号顶点只指向3、4号顶点这两个顶点，因此w小于0，w小于0不符合循环条件w>=0，因此不执行for循环，

最后就会调用print(v)函数把v号顶点输出->此时把2号顶点输出->所以得到的逆拓扑排序序列中第五个顶点是2号顶点，

至此，关于2号顶点的DFS函数执行完毕（2号顶点弹出递归栈），

如下图：

如上图，

现在就回到了DFSTraverse函数中的第二个for循环内，此时2号顶点和有关于2号顶点的操作全部结束，会继续往后遍历，

如果v号顶点没有被访问过即visited[v]为false，!visited[v]为true，那么就执行if语句并调用DFS函数，传入图G和v号顶点->（注：在上述图里，如果把某个顶点标为灰色，意味着该顶点的visited值为true即该顶点已经被访问过）此时图G中所有顶点都已经被访问过即visited[v]为true，!visited[v]为false，那么就不执行if语句，

至此，DFSTraverse函数中的第二个for循环结束，DFSTraverse函数结束，

图G的逆拓扑排序序列完成。