【机器学习】集成学习算法及实现过程
一、学习目标
- 了解什么是集成学习
- 了解机器学习中的两个核⼼任务
- 理解Bagging集成原理
- 理解随机森林构造过程
- 掌握RandomForestClassifier的使⽤
- 掌握boosting集成原理和实现过程
- 理解bagging和boosting集成的区别
- 理解AdaBoost集成原理
- 理解GBDT的算法原理
二、集成学习算法简介
2.1 机器学习两大核心任务(回顾)
- 任务一:如何优化训练数据及其目的 --> 目的主要用于解决:欠拟合问题
- 任务二:如何提升泛化能力及其目的 --> 目的主要用于解决:过拟合问题
2.2 什么是集成学习
-
含义:集成学习通过建立几个模型来解决单一预测问题。
-
工作原理:集成学习通过生成多个分类器/模型,各自独立地学习和做出预测。由这些预测结合形成组合预测,该组合预测将优于单个分类器。
-
举例说明:【三个臭皮匠顶个诸葛亮】

-
集成学习的必要性:
集成学习是机器学习中的一种思想,通过组合多个模型(弱学习器/基学习器)来形成一个精度更高的模型。训练时,依次使用训练集训练出这些弱学习器,预测时则联合这些弱学习器进行预测。

-
用代码来说明:
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets# 数据集:使用生成500个样本点,噪声参数设为0.3,随机种子固定为42保证可复现性。 # 数据特点:生成的双月牙形数据集具有明显非线性特征,噪声设置使分类更具挑战性。 X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=42)# 绘制图像 plt.scatter(X[y==0,0], X[y==0,1]) plt.scatter(X[y==1,0], X[y==1,1]) plt.show()
-
数据集划分:测试集和训练集
from sklearn.model_selection import train_test_splitX_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42) -
使用逻辑回归算法:分类器1
from sklearn.linear_model import LogisticRegressionlog_clf = LogisticRegression() log_clf.fit(X_train,y_train) log_clf.score(X_test,y_test)0.864
-
使用SVM支撑向量机:作为分类器2
from sklearn.svm import SVCsvm_clf = SVC() svm_clf.fit(X_train,y_train) svm_clf.score(X_test,y_test)0.896
-
使用决策树算法:作为分类器3
from sklearn.tree import DecisionTreeClassifierdt_clf = DecisionTreeClassifier() dt_clf.fit(X_train,y_train) dt_clf.score(X_test,y_test)0.856
-
算法预测及投票(少数服从多数)
-
投票机制:将三个模型的预测结果相加,则判定为1类,否则为0类。
-
技术细节:使用将布尔结果显式转换为整型,保证后续计算一致性。
log_clf_predict = log_clf.predict(X_test) svm_clf_predict = svm_clf.predict(X_test) dt_clf_predict = dt_clf.predict(X_test)log_clf_predict[:10]array([1, 0, 0, 1, 1, 1, 0, 0, 0, 0], dtype=int64)
svm_clf_predict[:10]array([0, 0, 0, 1, 1, 1, 0, 0, 0, 0], dtype=int64)
dt_clf_predict[:10]array([1, 0, 1, 1, 1, 1, 0, 0, 0, 0], dtype=int64)
-
-
投票:
将三个模型的预测结果相加,则判定为1类,否则为0类。# 将三个模型的预测结果相加,则判定为1类,否则为0类。 y_predict = np.array((log_clf_predict + svm_clf_predict + dt_clf_predict)>=2,dtype='int') y_predict[:10]array([1, 0, 0, 1, 1, 1, 0, 0, 0, 0])
# 计算模型准确度 from sklearn.metrics import accuracy_scoreaccuracy_score(y_test,y_predict)0.912
-
集成效果:投票集成后的准确率达到90.4%,超过所有单一模型表现。
-
提升原理:通过算法间的误差互补,降低了过拟合风险,增强模型鲁棒性。
-
使用sklearn中的VotingClassifier(Hard Voting)
from sklearn.ensemble import VotingClassifiervoting_clf = VotingClassifier(estimators=[("log_clf",LogisticRegression()),("svm_clf",SVC()),("dt_clf",DecisionTreeClassifier()) ],voting='hard')voting_clf.fit(X_train,y_train)
voting_clf.score(X_test,y_test)0.912
-
参数配置:
- estimators : 接收包含(名称,模型实例)元组的列表,示例包含逻辑回归、SVM和决策树
- voting: 表示使用硬投票(直接比较类别标签)
-
验证结果:接口实现的集成分类器准确率与手动实现完全一致(90.4%)
-
优化建议:实际应用中应先对各个基模型进行调参优化,再组合使用。
-
使用sklearn中的VotingClassifier(soft Voting)
voting_clf2 = VotingClassifier(estimators=[("log_clf",LogisticRegression()),("svm_clf",SVC(probability=True)), # 使用概率("dt_clf",DecisionTreeClassifier(random_state=666)) ],voting='soft')voting_clf2.fit(X_train,y_train)
voting_clf2.score(X_test,y_test)0.904
2.3 集成学习中Boosting(提升法)、Bagging(自助聚集法)和Stacking(堆叠法)
2.3.1 Boosting(提升算法)
-
含义:
Boosting 是一种通过迭代训练弱学习器,逐步提升模型预测能力的集成学习方法。
其核心思想是:让后续的弱学习器重点关注前序模型预测错误的样本,通过加权调整样本或学习器的权重,最终将多个弱学习器按权重组合成一个强学习器。
通俗来说:Boosting通过知错能改的迭代机制,将弱学习器逐步升级为强学习器,适合需要高精度的场景,但需注意过拟合风险(可通过正则化、早停等控制)。

-
产生背景:
- 弱学习器(如决策树桩)通常简单且预测能力有限,但计算成本低。
- 如何通过组合弱学习器提升性能?Boosting 通过自适应迭代,让每个新学习器聚焦于前序模型的缺陷,从而 “循序渐进” 地优化整体效果。
-
解决的问题:
- 分类与回归问题:通过迭代优化,提升模型对复杂数据分布的拟合能力。
- 欠拟合到过拟合的平衡:弱学习器本身不易过拟合,Boosting 通过调整权重避免单一模型的偏差,同时通过组合降低方差。
-
现实意义:
- 高精度模型构建:在结构化数据(如金融风控、医疗诊断)中表现优异,典型算法如 AdaBoost、Gradient Boosting(GBM)、XGBoost、LightGBM 已成为工业界标准工具。
- 可解释性增强:通过特征重要性分析(如 XGBoost 的 feature_importance),帮助理解数据中的关键驱动因素。
- 处理不平衡数据:通过调整样本权重,提升对少数类的识别能力(如 AdaBoost 的权重机制)。
-
实现方式:
- 迭代训练:
- 初始化样本权重(通常均匀分布)。
- 训练第 t t t个弱学习器,计算其在训练集上的错误率 e t e_t et。
- 根据错误率调整样本权重:预测错误的样本权重增加,正确的减少。
- 根据弱学习器的表现分配权重 α t \alpha_t αt(错误率越低,权重越高)。
- 重复步骤2-4,直至满足停止条件(如学习器数量达到上限)。
- 组合方式:最终模型为弱学习器的加权和,即
f ( x ) = ∑ t = 1 T α t h t ( x ) f(x) = \sum_{t=1}^T \alpha_t h_t(x) f(x)=∑t=1Tαtht(x)
(分类问题通常通过符号函数或投票决策,回归问题直接求和)。 - 典型算法:
- AdaBoost:通过指数损失函数调整样本权重。
- Gradient Boosting:利用梯度下降原理,将损失函数的负梯度作为残差,训练弱学习器拟合残差。
- 迭代训练:
2.3.2 Bagging(自助聚集算法)
-
1. 含义
Bagging(Bootstrap Aggregating)是一种通过自助采样(Bootstrap,统计学上称之为放回取样)生成多个独立训练集,并行训练弱学习器,最终通过投票或平均组合结果的集成方法。其核心思想是:利用样本随机性降低模型方差,提升泛化能力。
通俗来讲:Bagging通过“集体智慧”的并行机制,利用样本和特征的随机性降低方差,适合泛化能力优先、可并行计算的场景。

-
2. 产生背景
- 单一模型(如决策树)易受训练数据波动影响,导致方差较大(过拟合)。
- Bootstrap采样(有放回抽样)可生成多个不同的训练子集,减少模型对特定样本的依赖。
-
3. 解决的问题
- 降低模型方差:通过并行训练多个独立模型,平均化各自的预测偏差,避免单一模型过拟合。
- 处理高维数据:在特征维度较高时(如图像、文本),通过随机子空间(Random Subspace)进一步降低方差(如随机森林)。
-
4. 实际意义
- 简单高效的泛化能力:典型算法如随机森林(Random Forest)在结构化数据和非结构化数据中均表现稳定,且无需复杂调参。
- 并行计算支持:由于各学习器独立训练,可利用多核计算加速,适合大规模数据。
- 特征重要性评估:通过随机森林的OOB(袋外数据)或排列重要性,可量化特征对预测的贡献。
-
5. 实现方式
- 自助采样:
- 从原始数据集 D D D中有放回地随机采样 n n n个样本( n n n为原始样本数),生成 T T T个独立训练集 { D 1 , D 2 , … , D T } \{D_1, D_2, \dots, D_T\} {D1,D2,…,DT}。
- 每个训练集 D t D_t Dt训练一个弱学习器 h t ( x ) h_t(x) ht(x)。
- 组合方式:
- 分类问题:通过多数投票(Majority Voting)确定最终类别。
- 回归问题:通过简单平均或加权平均得到预测值。
- 扩展:随机森林(Random Forest)
在Bagging基础上,对每个弱学习器(决策树)进一步引入特征随机采样:- 每次分裂时,从全部特征中随机选择 k k k个特征( k ≪ 总特征数 k \ll \text{总特征数} k≪总特征数)作为候选分裂特征。
- 进一步增强学习器的独立性,降低方差。
- 自助采样:
-
6. 举例代码实现
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets# 数据集:使用生成500个样本点,噪声参数设为0.3,随机种子固定为42保证可复现性。 # 数据特点:生成的双月牙形数据集具有明显非线性特征,噪声设置使分类更具挑战性。 X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=42)# 绘制图像 plt.scatter(X[y==0,0], X[y==0,1]) plt.scatter(X[y==1,0], X[y==1,1]) plt.show()
# 数据集划分 from sklearn.model_selection import train_test_splitX_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42)# 使用bagging(放回取样) from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import BaggingClassifier# estimator:表示分类器类型(子模型类型); # n_estimators: 表示子模型的个数 # max_samples: 表示每个子模型放回取样的数量,每次取100个样本 # bootstrap:表示采用放回取样的方式 bagging_clf = BaggingClassifier(estimator=DecisionTreeClassifier(),n_estimators=100,max_samples=100,bootstrap=True) bagging_clf.fit(X_train,y_train)
bagging_clf.score(X_test,y_test)0.912
-
增加子模型数量->提高集成模型的准确度
# 调整参数n_estimators=7000,表示子模型增加到5000个 bagging_clf2 = BaggingClassifier(estimator=DecisionTreeClassifier(),n_estimators=5000,max_samples=100,bootstrap=True) bagging_clf2.fit(X_train,y_train)
bagging_clf2.score(X_test,y_test)0.912
2.3.3 Boosting(提升法)和Bagging(自助聚集法)对比
| 维度 | Boosting | Bagging |
|---|---|---|
| 学习方式 | 串行迭代(强依赖前序学习器) | 并行独立(无依赖) |
| 样本利用 | 自适应调整样本权重(聚焦难样本) | 自助采样生成独立子集 |
| 目标 | 降低偏差(提升拟合能力) | 降低方差(提升泛化能力) |
| 弱学习器类型 | 通常为低复杂度模型(如决策树桩) | 可为高方差模型(如未剪枝决策树) |
| 计算成本 | 较高(串行训练) | 较低(可并行) |
| 典型算法 | AdaBoost、GBM、XGBoost、LightGBM | 随机森林、Bagging决策树 |
| 适用场景 | 高精度需求(如结构化数据竞赛) | 快速预测、并行计算(如实时推荐系统) |
2.3.4 Stacking(堆叠集成)
- 原理:
- 第一层(基础层)使用多个不同的弱学习器(如决策树、逻辑回归、SVM)对训练集进行预测,生成新的特征向量(预测值)。
- 第二层(元层)使用一个模型(如线性回归、神经网络)将第一层的输出作为输入,训练一个“融合模型”。
- 关键细节:
- 为避免过拟合,常使用交叉验证生成第一层的预测值(如5折交叉验证,每个基础模型对每个样本生成5次预测,取平均作为最终输入)。
- 元模型需与基础模型不同(如基础模型是树模型,元模型可选线性模型)。
- 优点:融合不同类型模型的优势,理论上集成效果最强;
- 缺点:计算成本高,需谨慎处理过拟合。
2.3.5 Boosting、Bagging和Stacking对比
| 类别 | 核心思想 | 弱学习器关系 | 典型算法 | 代表应用 |
|---|---|---|---|---|
| Boosting | 串行训练弱学习器,每个新模型重点关注前序模型的错误样本,通过加权投票/加权求和集成。 | 强依赖(顺序生成) | AdaBoost、Gradient Boosting(GBM)、XGBoost、LightGBM、CatBoost | 结构化数据竞赛(如Kaggle) |
| Bagging | 并行训练弱学习器,通过随机采样(样本/特征)降低方差,最终通过简单投票/平均集成。 | 无依赖(并行生成) | 随机森林(Random Forest)、装袋(Bagging) | 图像分类、金融风控 |
| Stacking | 分阶段训练:第一层用基础模型预测,第二层用元模型融合第一层的输出结果。 | 分层依赖(两层结构) | Stacking、Blending | 多模型融合场景(如推荐系统) |
2.3.6 其他重要集成方法
1. Blending(混合集成)
- 简化版Stacking:
- 直接将训练集划分为两部分(如70%用于训练基础模型,30%用于生成融合特征)。
- 基础模型在70%数据上训练后,对30%数据和测试集生成预测值,作为元模型的输入。
- 优点:计算量低于Stacking,实现更简单;
- 缺点:依赖数据划分方式,泛化性略差。
2. Boosting与Bagging的结合变种
- Random Forest vs. Boosting Tree:
- 随机森林是Bagging的典型应用,但在生成弱学习器(决策树)时,额外引入了特征随机采样(每次分裂仅考虑部分特征),进一步降低方差。
- Gradient Boosting with Random Features:
- 部分Boosting算法(如LightGBM)在迭代过程中引入随机特征采样,结合了Bagging的“降噪”思想,提升泛化能力。
3. 基于动态权重的集成(Dynamic Ensemble)
- 原理:根据输入样本的特性,动态调整每个弱学习器的权重。
- 例如:对图像中的“简单样本”,使用轻量级模型(如浅层网络)预测;对“困难样本”,使用复杂模型(如ResNet)预测。
- 典型方法:
- Mixture of Experts(MoE):专家模型负责特定样本子集,门控模型(Gating Network)决定样本由哪个专家处理。
- Stacked Generalization with Attention:通过注意力机制为不同样本分配不同模型的权重。
4. 结构化数据集成(针对特定任务)
- 多模态集成:融合图像、文本、语音等不同模态数据的模型(如CLIP、AlBEF)。
- 时序数据集成:组合LSTM、Transformer、Prophet等模型预测时间序列(如股票价格、天气预测)。
2.3.7 集成学习的选择逻辑
- 根据数据特点选择:
- 结构化数据(如表格数据):优先使用Boosting(XGBoost/LightGBM)或随机森林。
- 图像/文本数据:优先使用Stacking(融合CNN/RNN与Transformer)或动态集成(如MoE)。
- 根据计算资源选择:
- 并行计算能力强:Bagging(随机森林)、Stacking(可并行训练基础模型)。
- 串行计算:Boosting(需顺序训练)。
- 根据任务需求选择:
- 实时预测:轻量级集成(如单模型或简单投票)。
- 高精度需求:复杂集成(如Stacking+超参数调优)。
- 应用场景
- Boosting:擅长降低偏差,适合处理欠拟合问题,需关注过拟合(通过正则化控制)。
- Bagging:擅长降低方差,适合处理高维噪声数据,随机森林是其“全能型”代表。
- Stacking/Blending:融合不同模型的优势,适合追求极致性能的场景,但需注意过拟合和计算成本。
- 其他方法:动态集成、多模态集成等扩展了集成学习在复杂场景下的应用。
因此,集成学习是一个庞大的技术体系,Boosting和Bagging只是其中最基础的两类方法,实际应用中需根据数据和任务灵活选择或组合使用。
三、入门案例代码实现过程
3.1 Boosting示例
示例1:AdaBoosting
-
AdaBoosting工作原理

简言之:算法利用前一轮弱模型的误差来更新样本权重,然后一轮一轮地迭代,将得到的弱分类器加权组合,使其准确度提高,损失函数值减小。通俗而言就是下一个模型弥补上一个模型所犯的错误。
-
代码实现
# 引入库 import numpy as np import matplotlib.pyplot as plt# 引入sklearn中的数据集 from sklearn import datasets# 获取到数据集和标签 X,y = datasets.make_moons(n_samples=500,noise=0.3,random_state=666)# 绘制图像 plt.scatter(X[y==0,0],X[y==0,1]) plt.scatter(X[y==1,0],X[y==1,1]) plt.show()
# 数据集的划分 from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)# 实例化AdaBoosting from sklearn.ensemble import AdaBoostClassifier from sklearn.tree import DecisionTreeClassifierada_clf = AdaBoostClassifier(estimator=DecisionTreeClassifier(max_depth=2),n_estimators=500,random_state=666) ada_clf.fit(X_train,y_train)
# 查看预测结果准确度 ada_clf.score(X_test,y_test)0.88
示例2:Gradient Boosting 梯度提升
-
Gradient Boosting简介

-
基本原理
- 迭代训练:它通过迭代地训练一系列弱学习器(通常是决策树)来逐步提升模型的性能。每一次迭代都专注于学习上一轮模型预测产生的误差。
- 累加模型:最终的预测结果是将所有迭代过程中训练出的模型的预测值累加起来得到的。
-
具体过程
- 第一步:首先训练第一个模型 m 1 m_1 m1,这个模型在训练集上进行学习,由于它是一个弱学习器,其预测结果必然会存在一定的误差,将这个误差记为 e 1 e_1 e1。
- 第二步:针对第一步产生的误差 e 1 e_1 e1 训练第二个模型 m 2 m_2 m2,目的是让 m 2 m_2 m2能够学习到 m 1 m_1 m1 预测错误的部分 ,从而纠正 m 1 m_1 m1的一些偏差, m 2 m_2 m2 训练完后也会产生新的误差 e 2 e_2 e2 。
- 第三步及后续:接着针对 e 2 e_2 e2训练第三个模型 m 3 m_3 m3,产生误差 e 3 e_3 e3,依此类推,不断重复这个过程,训练更多的模型。
- 最终预测:在所有模型都训练完成后,最终的预测结果就是把这些模型 m 1 + m 2 + m 3 + ⋯ m_1 + m_2 + m_3 + \cdots m1+m2+m3+⋯ 的预测值相加(在实际应用中,每个模型前面可能还会有一个权重系数,来调整各个模型在最终预测中的贡献)。

-
核心优势
- 高精度:通过不断拟合残差(即前面模型产生的误差),逐步减少整体预测误差,能够构建出非常精确的预测模型,在很多数据挖掘和机器学习竞赛中表现优异。
- 适用性广:可以处理多种类型的数据,包括数值型和类别型数据,并且对于复杂的非线性关系也能较好地建模。
-
应用场景
广泛应用于回归和分类问题,如在金融领域预测股票价格、信用风险评估;在医疗领域预测疾病发生概率;在电商领域预测用户购买行为等 。
-
代码实现
from sklearn.ensemble import GradientBoostingClassifiergb_clf = GradientBoostingClassifier(max_depth=2,n_estimators=30) gb_clf.fit(X_train,y_train)
gb_clf.score(X_test,y_test)0.904
示例3:XGBoost案例
-
XGBoost简介
XGBoost(eXtreme Gradient Boosting)即极致梯度提升,是由陈天奇等人开发的开源机器学习项目,是对梯度提升树(GBDT )算法的高效实现和改进版本。它在算法和工程上做了诸多优化,是一种基于树的集成学习方法 ,在各大数据科学比赛中表现优异,被广泛用于数据科学领域。 -
XGBoost特点:
- 高效性:在训练前对特征进行排序并存储为Block结构,可重复使用以减少计算量;还支持分布式计算和多线程并行处理,能大大加快训练速度。
- 准确性:通过对损失函数进行二阶泰勒展开,考虑了梯度变化的趋势,让模型拟合更快、精度更高;加入正则项来控制模型复杂度,降低过拟合风险 。
- 灵活性:可适用于多种机器学习任务,如分类、回归、排序和推荐等;还能自动处理缺失值和异常值等问题 。
简言之:高效处理大规模数据,内置正则化防止过拟合,支持并行计算。
-
XGBoost工作原理
XGBoost采用分步前向加性模型,其基本组成元素是决策树(称为“弱学习器” ),通过迭代地训练多个弱学习器,并将它们的预测结果相加,形成最终的强学习器。具体工作过程如下:- 目标函数构建:目标函数由损失函数和正则项两部分组成。损失函数衡量模型预测值与真实值之间的差异,反映模型对数据的拟合程度;正则项则对模型复杂度进行惩罚,控制模型的叶子节点数量和叶子结点输出值的大小,防止过拟合 。
- 泰勒二阶展开:直接求解目标函数比较困难,XGBoost对目标函数进行泰勒二阶展开,将其转化为一种近似的表示形式。通过泰勒展开,能利用损失函数的一阶导数和二阶导数信息,更准确地近似目标函数,为后续决策树的构建提供指导 。
- 决策树生成:在每次迭代中,基于上一轮模型的预测残差(即真实值与上一轮模型预测值的差值 )训练一棵新的决策树。构建决策树时,从根节点开始,尝试对每个特征的不同取值进行分裂,依据从损失函数推导出来的节点分裂指标(如增益等 ),寻找能使目标函数下降最快的分裂方式,确定最优的分裂属性和分裂点,直到满足停止条件(如叶子节点数量达到上限、损失函数下降幅度小于阈值等 )。
- 模型迭代优化:每生成一棵决策树,就将其预测结果加入到整体模型中,更新模型的预测值;然后基于新的预测值与真实值的残差,继续训练下一棵决策树,不断迭代这个过程,逐步提升模型的预测性能 。
- 最终预测:当达到预设的迭代次数或满足其他停止条件时,迭代结束。最终的预测结果是将所有决策树的预测值累加起来得到(对于分类问题,可能还需进一步通过激活函数等方式转换为概率或类别 )。
-
实现方式1:scikit-learn 接口(XGBClassifier,无早停)
import numpy as np import matplotlib.pyplot as plt import xgboost as xgb from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, confusion_matrix import seaborn as sns# ---------------------- 1. 数据加载与预处理 ---------------------- iris = load_iris() # 加载鸢尾花数据集(150样本,4特征,3分类) X, y = iris.data, iris.target # X: 特征矩阵(150x4),y: 类别标签(0/1/2)# 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, # 30%数据作为测试集random_state=42 # 固定随机种子确保结果可复现 )# ---------------------- 2. 模型构建与训练 ---------------------- # 创建XGBoost分类器(scikit-learn接口) model = xgb.XGBClassifier(n_estimators=100, # 树的数量(迭代次数)learning_rate=0.1, # 学习率:控制每棵树的贡献度max_depth=3, # 树的最大深度(防止过拟合)objective='multi:softmax', # 多分类目标函数num_class=3, # 类别数(必须指定)random_state=42, # 固定随机种子n_jobs=-1 # 使用所有CPU核心并行训练 )# 训练模型 model.fit(X_train, y_train, # 训练数据eval_set=[(X_test, y_test)], # 评估集(用于监控训练过程)verbose=0 # 关闭训练日志输出 )# ---------------------- 3. 模型预测与评估 ---------------------- y_pred = model.predict(X_test) # 预测类别标签 accuracy = accuracy_score(y_test, y_pred) # 计算准确率 print(f"XGBoost (sklearn接口) 准确率: {accuracy:.4f}")# ---------------------- 4. 可视化:特征重要性 ---------------------- plt.figure(figsize=(10, 6)) xgb.plot_importance(model, importance_type='gain', # 基于分裂增益计算重要性title='特征重要性',xlabel='重要性分数',ylabel='特征名称') plt.tight_layout() plt.show()# ---------------------- 5. 可视化:混淆矩阵 ---------------------- plt.figure(figsize=(8, 6)) cm = confusion_matrix(y_test, y_pred) sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',xticklabels=iris.target_names,yticklabels=iris.target_names) plt.xlabel('预测类别') plt.ylabel('真实类别') plt.title('XGBoost分类结果混淆矩阵') plt.show()# ---------------------- 6. 可视化:决策边界(仅使用前两个特征) ---------------------- # 仅使用前两个特征进行2D可视化 X_vis = X[:, :2] X_train_vis, X_test_vis, y_train_vis, y_test_vis = train_test_split(X_vis, y, test_size=0.3, random_state=42 )# 训练仅使用前两个特征的模型 model_vis = xgb.XGBClassifier(**model.get_params()) model_vis.fit(X_train_vis, y_train_vis)# 创建网格数据 h = 0.02 # 网格步长 x_min, x_max = X_vis[:, 0].min() - 1, X_vis[:, 0].max() + 1 y_min, y_max = X_vis[:, 1].min() - 1, X_vis[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# 预测网格点的类别 Z = model_vis.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape)# 设置中文显示 plt.rcParams["font.family"] = ["SimHei"] plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题# 绘制决策边界 plt.figure(figsize=(10, 8)) plt.contourf(xx, yy, Z, alpha=0.4, cmap=plt.cm.coolwarm) plt.scatter(X_vis[:, 0], X_vis[:, 1], c=y, alpha=0.8, cmap=plt.cm.coolwarm, edgecolors='k') plt.xlabel('Sepal length (cm)') # 萼片长度 plt.ylabel('Sepal width (cm)') # 萼片宽度 plt.title('XGBoost决策边界可视化') plt.colorbar(ticks=[0, 1, 2], label='类别') plt.show()XGBoost (sklearn接口) 准确率: 1.0000



-
XGBoost关键参数解释
n_estimators:弱学习器数量(树的数量),过大会导致过拟合。learning_rate:学习率,控制每次迭代的步长,较小值需更多迭代。max_depth:树的最大深度,控制模型复杂度。
-
实现方式2:原生 API(xgboost.train (),支持早停)
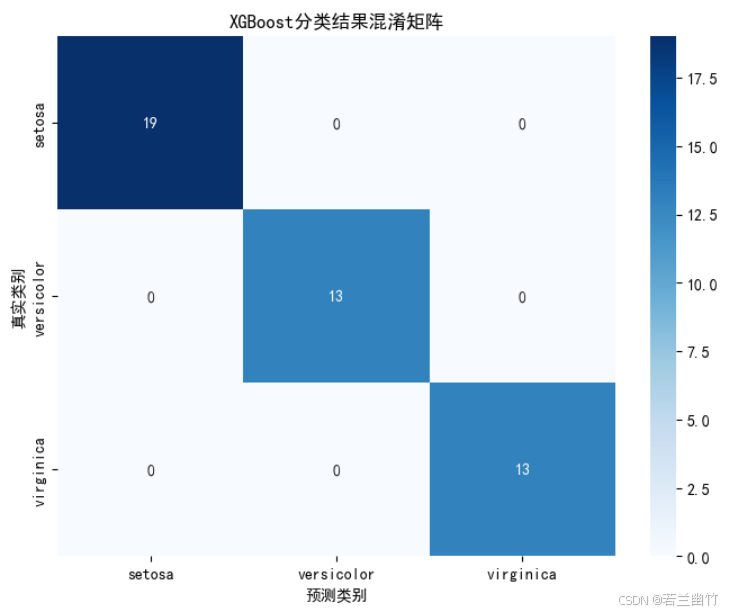
import numpy as np import matplotlib.pyplot as plt import xgboost as xgb from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, confusion_matrix import seaborn as sns# ---------------------- 1. 数据加载与预处理 ---------------------- iris = load_iris() X, y = iris.data, iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42 )# ---------------------- 2. 数据格式转换(原生API要求) ---------------------- dtrain = xgb.DMatrix(X_train, label=y_train) # 训练数据 dtest = xgb.DMatrix(X_test, label=y_test) # 测试数据# ---------------------- 3. 定义模型参数 ---------------------- params = {'objective': 'multi:softmax', # 多分类目标(输出类别标签)'num_class': 3, # 类别数'eval_metric': 'merror', # 评估指标:多分类错误率'max_depth': 3, # 树的最大深度'eta': 0.1, # 学习率(步长收缩因子)'subsample': 0.8, # 样本采样比例'colsample_bytree': 0.8, # 特征采样比例'random_state': 42 # 随机种子 }# ---------------------- 4. 训练模型(支持早停) ---------------------- evals_result = {} # 存储训练过程中的评估结果 model = xgb.train(params=params,dtrain=dtrain,num_boost_round=100, # 最大迭代次数evals=[(dtrain, 'train'), (dtest, 'test')], # 训练集和测试集上的评估evals_result=evals_result, # 保存评估结果early_stopping_rounds=10, # 早停:若10轮无提升则停止verbose_eval=0 # 关闭训练日志 )# ---------------------- 5. 模型预测与评估 ---------------------- y_pred = model.predict(dtest) # 预测类别标签 accuracy = accuracy_score(y_test, y_pred) print(f"XGBoost (原生API) 准确率: {accuracy:.4f}") print(f"最佳迭代轮数: {model.best_iteration}") # 早停时的最佳迭代轮数# ---------------------- 6. 可视化:训练过程中的评估指标 ---------------------- # 设置中文显示 plt.rcParams["font.family"] = ["SimHei"] plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题plt.figure(figsize=(10, 6)) plt.plot(evals_result['train']['merror'], label='训练集错误率') plt.plot(evals_result['test']['merror'], label='测试集错误率') plt.xlabel('迭代轮数') plt.ylabel('多分类错误率') plt.title('XGBoost训练过程中的错误率变化') plt.legend() plt.grid(True) plt.show()# ---------------------- 7. 可视化:特征重要性 ---------------------- plt.figure(figsize=(10, 6)) xgb.plot_importance(model, importance_type='gain', # 基于分裂增益计算重要性title='特征重要性',xlabel='重要性分数',ylabel='特征名称') plt.tight_layout() plt.show()# ---------------------- 8. 可视化:混淆矩阵 ---------------------- plt.figure(figsize=(8, 6)) cm = confusion_matrix(y_test, y_pred) sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',xticklabels=iris.target_names,yticklabels=iris.target_names) plt.xlabel('预测类别') plt.ylabel('真实类别') plt.title('XGBoost分类结果混淆矩阵') plt.show()# ---------------------- 9. 可视化:决策树结构(选第一棵树) ---------------------- plt.figure(figsize=(20, 15)) xgb.plot_tree(model, tree_idx=0, rankdir='LR') # LR: 从左到右布局 plt.title('XGBoost决策树结构(第一棵树)') plt.tight_layout() plt.show()XGBoost (原生API) 准确率: 1.0000
最佳迭代轮数: 1



-
关键注释对比
| 维度 | 方案1(scikit-learn接口) | 方案2(原生API) |
|---|---|---|
| 数据格式 | 直接使用numpy数组 | 必须转换为DMatrix(提升计算效率) |
| 参数体系 | 与sklearn兼容(如n_estimators) | 原生参数(如num_boost_round、eval_metric) |
| 早停实现 | 不支持(需通过外部库间接实现) | 内置支持(evals+early_stopping_rounds) |
| 预测输出 | predict()直接返回类别标签 | 根据objective类型返回标签或概率 |
| 适用场景 | 快速集成到sklearn工作流(如管道、交叉验证) | 需要精细控制训练过程(如自定义损失、早停) |
通过注释可清晰看到两种API的差异,实际使用时需根据需求选择:
-
简单场景:优先使用scikit-learn接口,代码更简洁。
-
高级需求:使用原生API,解锁早停、自定义损失函数等特性。
-
可视化代码解释
-
特征重要性图:
- 使用
xgb.plot_importance展示各特征在模型中的重要性(基于分裂增益)。 - 帮助理解哪些特征对预测结果影响最大(如鸢尾花数据中,花瓣长度通常是最重要的特征)。
- 使用
-
混淆矩阵:
- 使用
seaborn.heatmap可视化模型在各类别上的预测准确性。 - 对角线表示正确预测数,非对角线表示错误分类情况。
- 使用
-
决策边界图(仅方案1):
- 仅使用前两个特征(萼片长度和宽度)训练模型,绘制2D决策边界。
- 直观展示模型如何划分特征空间,不同颜色区域对应不同类别预测。
-
训练过程图(仅方案2):
- 绘制训练集和测试集上的错误率随迭代轮数的变化曲线。
- 可观察模型是否过拟合(训练误差下降但测试误差上升)或欠拟合(误差未收敛)。
-
决策树结构图(仅方案2):
- 使用
xgb.plot_tree可视化单棵决策树的结构(默认展示第一棵树)。 - 展示树的分裂条件和叶子节点的预测值,解释模型决策逻辑。
- 使用
3.2 Bagging:随机森林案例
-
算法:Random Forest(随机森林)
-
特点:通过自助采样和特征随机选择构建多个决策树,降低方差。
-
代码示例:如下所示
from sklearn.datasets import load_iris # 导入鸢尾花数据集(150样本,4特征,3分类) from sklearn.model_selection import train_test_split # 划分训练集和测试集 from sklearn.ensemble import RandomForestClassifier # 导入随机森林分类器 from sklearn.metrics import accuracy_score # 计算分类准确率的指标# ---------------------- 1. 数据加载与预处理 ---------------------- iris = load_iris() # 加载经典鸢尾花数据集 X, y = iris.data, iris.target # X: 特征矩阵(150x4),y: 类别标签(0/1/2)# 划分训练集和测试集 # test_size=0.3: 30%数据作为测试集 # random_state=42: 固定随机种子,确保结果可复现 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42 )# ---------------------- 2. 模型构建与训练 ---------------------- # 创建随机森林分类器(Bagging集成方法) model = RandomForestClassifier(n_estimators=100, # 森林中树的数量(弱学习器数量)max_features='sqrt', # 每棵树随机选择的特征数(sqrt(总特征数))max_depth=None, # 树的最大深度(None表示不限制,直到叶子纯或最小样本数)min_samples_split=2, # 分裂内部节点所需的最小样本数min_samples_leaf=1, # 叶子节点所需的最小样本数bootstrap=True, # 是否使用自助采样(Bagging核心)oob_score=False, # 是否使用袋外数据评估模型(此处关闭)random_state=42, # 固定随机种子n_jobs=-1 # 使用所有CPU核心并行训练 )# 训练模型 model.fit(X_train, y_train) # 输入训练数据和标签# ---------------------- 3. 模型预测与评估 ---------------------- y_pred = model.predict(X_test) # 对测试集进行预测,输出类别标签 accuracy = accuracy_score(y_test, y_pred) # 计算准确率(正确预测样本数/总样本数)# 输出结果 print(f"随机森林准确率: {accuracy:.4f}") # 通常>95%# ---------------------- 4. 模型解释与特征重要性 ---------------------- # 特征重要性:每个特征对模型决策的贡献度 importances = model.feature_importances_ feature_names = iris.feature_names# 打印特征重要性排名 print("\n特征重要性排名:") for i, (name, importance) in enumerate(sorted(zip(feature_names, importances), key=lambda x: -x[1])):print(f"{i+1}. {name}: {importance:.4f}")# 可选:可视化特征重要性 import matplotlib.pyplot as plt# 设置中文显示 plt.rcParams["font.family"] = ["SimHei"] plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题plt.bar(feature_names, importances) plt.xticks(rotation=45) plt.title('特征重要性') plt.show()随机森林准确率: 1.0000
特征重要性排名:
- petal width (cm): 0.4340
- petal length (cm): 0.4173
- sepal length (cm): 0.1041
- sepal width (cm): 0.0446

-
随机森林参数:
n_estimators:树的数量,通常越大效果越好(但计算成本更高)。max_features:每次分裂时随机选择的特征数,降低方差。
-
关键注释说明:
-
数据处理:
train_test_split的random_state确保每次划分结果相同,便于复现实验。- 鸢尾花数据集包含4个特征(花瓣长度/宽度、萼片长度/宽度)和3个类别(Setosa、Versicolour、Virginica)。
-
随机森林核心参数:
n_estimators:树的数量,通常越大效果越好(但计算成本更高)。max_features='sqrt':每棵树随机选择 总特征数 \sqrt{\text{总特征数}} 总特征数 个特征,降低树之间的相关性。bootstrap=True:启用自助采样(Bagging的核心),每个树使用不同的样本子集训练。
-
特征重要性:
model.feature_importances_:基于特征在树中分裂时的信息增益计算重要性。- 重要性越高的特征,对模型预测的贡献越大。
-
Bagging机制:
- 随机森林通过样本随机(自助采样)和特征随机(随机选择特征子集)构建多棵树。
- 最终预测结果通过多数投票(分类)或平均(回归)集成。
-
3.3 Stacking:多层模型融合案例
-
算法:StackingClassifier(scikit-learn 实现)
-
特点:分两层训练,第一层使用多个基础模型,第二层使用元模型融合结果。

训练二层模型的过程:数据集被分成2份,第一份作为第一层的模型输入,第二份+第一层模型的输出作为第二层的模型输入
-
扩展:构建更复杂的模型

训练三层模型的过程:数据集被分成三份,第一份作为第一层的模型输入,第二份作为第二层模型的输入,第三份+第二层的输出作为第三层的模型输入
-
实现方案1:
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.ensemble import StackingClassifier, RandomForestClassifier from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score# 加载数据 iris = load_iris() X, y = iris.data, iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 定义基础模型 estimators = [('rf', RandomForestClassifier(n_estimators=100, random_state=42)),('svm', SVC(probability=True, random_state=42)),('dt', DecisionTreeClassifier(random_state=42)) ]# 创建Stacking模型(第二层使用逻辑回归作为元模型) model = StackingClassifier(estimators=estimators,final_estimator=LogisticRegression(random_state=42) ) model.fit(X_train, y_train)# 预测与评估 y_pred = model.predict(X_test) accuracy = accuracy_score(y_test, y_pred) print(f"Stacking Accuracy: {accuracy:.4f}") # 通常>95%Stacking Accuracy: 1.0000
-
Stacking参数:
estimators:基础模型列表,需包含名称和模型实例。final_estimator:元模型,通常选择简单模型(如逻辑回归)。
-
实现方案2:
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.ensemble import StackingClassifier, RandomForestClassifier from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score, confusion_matrix, classification_report import seaborn as sns from matplotlib.colors import ListedColormap# ---------------------- 1. 数据加载与预处理 ---------------------- iris = load_iris() # 加载经典鸢尾花数据集(150样本,4特征,3分类) X, y = iris.data, iris.target # X: 特征矩阵(150x4),y: 类别标签(0/1/2)# 为可视化仅选择前两个特征(花瓣长度和宽度) X_vis = X[:, :2] # 只取前两个特征用于2D可视化 X_train_vis, X_test_vis, y_train_vis, y_test_vis = train_test_split(X_vis, y, test_size=0.3, random_state=42 )# 完整数据集用于模型训练 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42 )# ---------------------- 2. 定义基础模型(第一层) ---------------------- # 每个基础模型将对数据进行独立学习并生成预测 estimators = [('rf', RandomForestClassifier(n_estimators=100, # 随机森林树的数量max_features='sqrt', # 每棵树随机选择的特征数random_state=42 # 固定随机种子确保结果可复现)),('svm', SVC(probability=True, # 启用概率估计(需要计算类别概率)kernel='rbf', # 使用径向基函数核random_state=42)),('dt', DecisionTreeClassifier(max_depth=3, # 限制树的深度防止过拟合random_state=42)) ]# ---------------------- 3. 创建Stacking模型(第二层) ---------------------- # 元模型将基础模型的预测结果作为输入,学习如何组合这些结果 model = StackingClassifier(estimators=estimators, # 基础模型列表final_estimator=LogisticRegression( # 元模型:逻辑回归penalty='l2', # L2正则化防止过拟合C=1.0, # 正则化强度倒数random_state=42),cv=5, # 5折交叉验证生成基础模型的预测passthrough=False # 元模型仅使用基础模型的预测结果,不包含原始特征 )# ---------------------- 4. 模型训练与评估 ---------------------- model.fit(X_train, y_train) # 训练Stacking模型# 预测 y_pred = model.predict(X_test) # 预测类别标签 y_pred_proba = model.predict_proba(X_test) # 预测类别概率# 评估 accuracy = accuracy_score(y_test, y_pred) # 计算准确率 print(f"Stacking模型准确率: {accuracy:.4f}")# 打印分类报告(精确率、召回率、F1分数) print("\n分类报告:") print(classification_report(y_test, y_pred, target_names=iris.target_names))# ---------------------- 5. 可视化:决策边界 ---------------------- # 创建网格以绘制决策边界 h = 0.02 # 网格步长 x_min, x_max = X_vis[:, 0].min() - 1, X_vis[:, 0].max() + 1 y_min, y_max = X_vis[:, 1].min() - 1, X_vis[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# 训练仅使用前两个特征的可视化模型 model_vis = StackingClassifier(estimators=[(name, est) for name, est in estimators],final_estimator=LogisticRegression(random_state=42) ) model_vis.fit(X_train_vis, y_train_vis) Z = model_vis.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape)# 绘制决策边界 plt.figure(figsize=(12, 10)) cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])plt.contourf(xx, yy, Z, cmap=cmap_light, alpha=0.8) plt.scatter(X_vis[:, 0], X_vis[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20) plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.title("Stacking模型的决策边界") plt.xlabel('Sepal length (cm)') # 萼片长度 plt.ylabel('Sepal width (cm)') # 萼片宽度# 添加图例 plt.legend(handles=[plt.Line2D([0], [0], marker='o', color='w', label=iris.target_names[0], markerfacecolor='#FF0000', markersize=10),plt.Line2D([0], [0], marker='o', color='w', label=iris.target_names[1], markerfacecolor='#00FF00', markersize=10),plt.Line2D([0], [0], marker='o', color='w', label=iris.target_names[2], markerfacecolor='#0000FF', markersize=10) ])# ---------------------- 6. 可视化:混淆矩阵 ---------------------- plt.figure(figsize=(10, 8)) cm = confusion_matrix(y_test, y_pred) sns.heatmap(cm, annot=True, fmt="d", cmap="Blues", xticklabels=iris.target_names, yticklabels=iris.target_names) plt.title("Stacking模型的混淆矩阵") plt.xlabel("预测类别") plt.ylabel("真实类别")plt.tight_layout() plt.show()# ---------------------- 7. 可视化:基础模型与Stacking对比 ---------------------- plt.figure(figsize=(15, 10))# 为每个基础模型绘制决策边界 for i, (name, est) in enumerate(estimators):plt.subplot(2, 2, i+1)# 训练模型est_vis = est.__class__(**est.get_params())est_vis.fit(X_train_vis, y_train_vis)Z = est_vis.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, cmap=cmap_light, alpha=0.8)plt.scatter(X_vis[:, 0], X_vis[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20)plt.title(f"{name.upper()}的决策边界")plt.xlabel('Sepal length (cm)')plt.ylabel('Sepal width (cm)')# 绘制Stacking模型的决策边界 plt.subplot(2, 2, 4) plt.contourf(xx, yy, Z, cmap=cmap_light, alpha=0.8) plt.scatter(X_vis[:, 0], X_vis[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20) plt.title("Stacking模型的决策边界") plt.xlabel('Sepal length (cm)') plt.ylabel('Sepal width (cm)')plt.tight_layout() plt.show()Stacking模型准确率: 1.0000
分类报告:
precision recall f1-score supportsetosa 1.00 1.00 1.00 19 versicolor 1.00 1.00 1.00 13virginica 1.00 1.00 1.00 13accuracy 1.00 45macro avg 1.00 1.00 1.00 45weighted avg 1.00 1.00 1.00 45



一、核心指标解释
1. precision(精确率)
- 定义:在预测为某类的样本中,真正属于该类的比例。
precision = TP TP + FP \text{precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} precision=TP+FPTP
(TP:真阳性,FP:假阳性) - 意义:反映模型对某类样本的预测准确性,避免误判。
2. recall(召回率)
- 定义:在实际属于某类的样本中,被正确预测为该类的比例。
recall = TP TP + FN \text{recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} recall=TP+FNTP
(FN:假阴性) - 意义:反映模型对某类样本的捕捉能力,避免漏判。
3. f1-score(F1分数)
- 定义:精确率和召回率的调和平均数,综合衡量模型性能。
F 1 = 2 × precision × recall precision + recall F1 = 2 \times \frac{\text{precision} \times \text{recall}}{\text{precision} + \text{recall}} F1=2×precision+recallprecision×recall - 意义:当精确率和召回率差异较大时,F1分数能更平衡地评估模型。
4. support
-
定义:该类样本的真实数量(测试集中的实际样本数)。
-
意义:用于判断指标的可靠性(样本量越大,指标越可信)。
-
关键注释说明:
-
数据处理:
- 创建两个版本的数据集:完整数据集用于模型训练,仅含前两个特征的数据集用于2D可视化。
- 使用
train_test_split时固定random_state确保结果可复现。
-
Stacking核心机制:
- 第一层(基础模型):随机森林、SVM和决策树分别对数据建模。
- 第二层(元模型):逻辑回归学习如何组合基础模型的预测结果。
cv=5:使用5折交叉验证生成基础模型的预测,避免数据泄露。
-
可视化部分:
- 决策边界图:直观展示模型如何划分特征空间。
- 混淆矩阵:显示各类别的预测准确性,对角线元素表示正确预测数。
- 对比图:将Stacking模型与基础模型的决策边界进行对比,突出集成优势。
-
评估指标:
- 准确率:整体预测正确的比例。
- 分类报告:包含精确率、召回率和F1分数,按类别细分评估。
