高性能算法RIME：基于物理的优化的霜冰优化算法

1.简介

文章提出了一种基于雾状冰物理现象的高效优化算法，称为RIME。RIME算法通过模拟雾状冰的软雾状和硬雾状生长过程，构建软雾状搜索策略和硬雾状穿刺机制，实现优化方法中的探索和开发行为。同时，改进了算法中的贪心选择机制，在选择最优解阶段更新种群，增强了RIME的开发能力。

2. 雾冰形成的灵感

雾晶冰是空气中积聚的水汽尚未凝结而成的，它在低温下结冰并粘附在树枝等物体上，由于其独特的气候特征和地形地貌，一些地区每年形成雾晶冰般的独特景观，如图1所示。

图1 雾气冰实景
霜冰的生长过程由温度、风速、湿度、空气等因素决定，霜的形成在不同条件下有所不同。同时，由于环境因素和生长模式的影响，雾凇冰不能无限期生长，当它达到相对稳定的状态时就会停止生长。雾凇的生长模式一般分为两种：软雾凇和硬雾凇，主要取决于形成过程中的风速，如图2所示，其中ΔABC表示雾凇生长平面，D1、D2、D3、D4表示雾霭的出生点。通常，软霜是在微风环境中产生的，硬霜是在大风环境中形成的。如图2（a）所示，微风的特点是风速小、风向多变，风同时存在于同一高度平面的各个方向。因此，微风形成的柔软霜缓慢而随机地生长。另一方面，大风的特点是风速高，同一高度平面内风向大致相同，如图2（b）所示。因此，大风形成的硬霜速度很快，生长方向大致相同。

图2.不同环境下软雾状和硬雾状的形成过程。

研究受雾状冰生长机制的启发，提出了一种通过模拟软雾状粒子运动进行算法搜索的软雾状搜索策略。此外，提出了一种硬雾状穿刺机制，通过模拟硬雾状代理之间的交叉行为来利用该算法。最后，改进了元启发式算法的选择机制，提出了正贪婪选择机制。本文结合上述三种机制提出了性能更好的RIME算法。

3. RIME的数学模型

通过分析风速、冻结系数、附着材料的横截面积和生长时间的影响，模拟了每个雾化器条带的生长过程。另一方面，受模拟金属颗粒聚集的扩散限制聚集[50]方法的启发，通过对每个雾化器颗粒的运动行为建模，模拟了每个雾化器颗粒凝聚成雾化器剂的运动过程，最终生成的雾化器剂呈条状晶体的形式。RIME由四个阶段组成：雾化器簇的初始化、提出的软雾化器搜索策略、提出的硬雾化器穿刺机制和贪婪选择机制的改进。

3.1 冰晶簇初始化

受现实启发，本文将每个冰晶视为算法中的搜索代理，所有代理形成的冰晶群体作为算法的种群。首先，初始化整个冰晶群体$R$。冰晶群体由$n$个冰晶代理$S_i$组成，每个冰晶代理由$d$个冰晶粒子$x_{ij}$组成，如图3和公式(1)所示。因此，冰晶群体$R$可以直接由冰晶粒子$x_{ij}$表示，如公式(2)所示。

$$R=\left[\begin{array}{c}{S}_1\\ S_2\\ ⋮\\ S_i\end{array}\right];S_i=x_{i1}{x}_{i2}\cdots x_{ij}$$

$$R=\left[\begin{array}{c}{x}_{11}{x}_{12}\cdots x_{1j}\\ x_{21}{x}_{22}\cdots x_{2j}\\ ⋮\\ x_{i1}{x}_{i2}\cdots x_{ij}\end{array}\right]$$

其中$i$是冰晶代理的序号，$j$是冰晶粒子的序号。此外，$F(S_i)$用于表示每个冰晶代理的生长状态，即元启发式算法中代理的适应度值。

图3.雾化器空间的初始化。

3.2 软冰晶搜索策略

在微风环境中，软冰晶的生长是随机的，冰晶粒子可以自由覆盖附着物体表面的大部分区域，但在同一方向上生长缓慢。受软冰晶生长的启发，本研究提出了一种软冰晶搜索策略，利用冰晶粒子的强随机性和覆盖能力，使算法在早期迭代中快速覆盖整个搜索空间，不易陷入局部最优。

当冰晶粒子凝聚成软冰晶代理时，具有以下特征：

1. 在粒子凝聚形成软冰晶代理之前，每个粒子$x_{ij}$将根据一定规律游荡，游荡的效率受环境因素影响。

2. 如果自由态冰晶粒子移动到软冰晶代理附近，它们将与代理中的粒子凝聚，从而使软冰晶代理的稳定性发生变化。

3. 两个粒子中心之间的距离是固定的，凝聚程度在每个粒子之间有所不同。

4. 如果粒子直接移动到逃逸半径之外，则不会发生粒子间凝聚。

5. 在软冰晶形成过程中，每个粒子的随机凝聚增加了代理附着的区域，从而增加了自由粒子凝聚的概率。然而，代理不会无限生长，最终会因环境因素达到稳定状态。

在本文中，根据冰晶粒子的五种运动特性，每个粒子的凝聚过程被简洁地模拟，如图4所示，冰晶粒子的位置计算如公式(3)所示。

$$R_{ij}^{new}=R_{best,j}+r_1\cdot \cos \theta \cdot \beta \cdot h\cdot U{b}_{ij}\cdot L{b}_{ij}+L{b}_{ij},r_2<E$$

其中，$R_{ij}^{new}$是更新粒子的新位置，$i$和$j$分别表示第$i$个冰晶代理的第$j$个粒子。$R_{best,i}$是冰晶群体$R$中最佳冰晶代理的第$j$个粒子。参数$r_1$是范围(-1,1)内的随机数，$r_1$控制粒子运动的方向，$\cos \theta$将随着迭代次数的变化而变化，如公式(4)所示。$\beta$是环境因子，随着迭代次数的变化来模拟外部环境的影响，并用于确保算法的收敛，如公式(5)所示。$h$是粘附度，是范围(0,1)内的随机数，用于控制两个冰晶粒子中心之间的距离。

$$\theta =\pi \cdot \frac{t}{10\cdot T}$$

其中$t$是当前迭代次数，$T$是算法的最大迭代次数。

$$\beta =1-\frac{w\cdot t}{T}/w$$

其中$\beta$的数学模型是步进函数，$\cdot$表示四舍五入；默认$w$值为5，用于控制步进函数的段数。返回公式(3)，$U{b}_{ij}$和$L{b}_{ij}$分别是逃逸空间的上下界。$E$是附着系数，影响代理的凝聚概率，并随着迭代次数的增加而增加，如公式(6)所示。

$$E=\sqrt{\frac{t}{T}}$$

$r_2$是范围(0,1)内的随机数，与$E$一起控制粒子是否凝聚，即粒子位置是否更新。软冰晶搜索策略的伪代码如算法1所示。


图4 软雾状颗粒运动

3.3 硬冰晶穿刺机制

在强风条件下，硬冰晶的生长比软冰晶生长更简单、更规则。当冰晶粒子凝聚成硬冰晶时，具有以下特征：1）风速非常强，以至于其他影响可以忽略不计，导致不同的硬冰晶代理朝同一方向飘雪。2）由于生长方向相同，每个冰晶代理可以很容易地交叉，这种现象称为冰晶穿刺。3）与软冰晶代理一样，硬冰晶代理随着生长而增大，导致在更好生长条件下代理间穿刺的概率更大。

因此，本文受穿刺现象启发，提出了一种硬冰晶穿刺机制，可用于更新算法中代理之间的信息，以便算法粒子可以交换，从而提高算法的收敛性和跳出局部最优的能力。穿刺现象如图5所示，粒子间替换的公式如公式(7)所示。

$$R_{ij}^{new}=R_{best,j}\cdot r_3<F^{norm}(S_i)$$

其中$R_{ij}^{new}$是更新粒子的新位置，$R_{best,i}$是冰晶群体$R$中最佳冰晶代理的第$j$个粒子。$F^{norm}(S_i)$表示当前代理适应度值的归一化值，表示第$i$个冰晶代理被选择的概率。$r_3$是范围(-1,1)内的随机数。

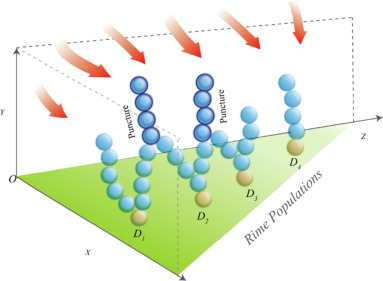
硬冰晶穿刺机制

3.4 正向贪婪选择机制

通常，元启发式优化算法具有贪婪选择机制，该机制在每次更新后替换并记录最佳适应度值和最佳代理。典型的想法是比较代理的更新适应度值与全局最优值，并在更新值优于当前全局最优值时替换最优适应度值，并将代理记录为最优。这种操作的优点在于它简单快捷，但无助于种群的探索和开发，仅作为记录。

因此，本文提出了一种激进的贪婪选择机制，用于参与种群更新以提高全局探索效率。具体思想是比较代理更新前的适应度值与更新后的适应度值，如果更新后的适应度值优于更新前的值，则替换两者的解。一方面，该机制允许种群通过活跃代理替换不断拥有优秀代理，从而提高全局解的质量。另一方面，随着每次迭代，代理在种群中的位置显著变化，不可避免地会有比更新前种群更差的代理，并被排除在下一次迭代之外。因此，此操作可用于确保种群在每次迭代中朝着更优方向进化。

本文中，解决最小值问题的正向贪婪选择机制的伪代码，如算法3所示。

算法3 正向贪婪选择机制的伪代码

3.5 提出的RIME算法

总之，首先，受软冰晶粒子运动启发，在本节中设计了一种独特的逐步搜索和开发方法，作为算法的核心优化搜索方法。随后，受硬冰晶交叉启发，提出了一种硬冰晶穿刺机制，以实现普通代理和最优代理之间的维度交叉，从而提高算法的解精度。最后，基于贪婪选择机制，提出了一种改进的正向贪婪选择机制，以尽可能通过改变最优解的选择来增加种群的多样性并防止算法陷入局部最优。算法的整体结构以伪代码和流程图的形式展示。伪代码如算法4所示。
算法4 RIME的伪代码

%%
function [Best_rime_rate,Best_rime,Convergence_curve]=RIME(N,Max_iter,lb,ub,dim,fobj)% initialize positionBest_rime=zeros(1,dim);Best_rime_rate=inf;%change this to -inf for maximization problemsRimepop=initialization(N,dim,ub,lb);%Initialize the set of random solutionsLb=lb.*ones(1,dim);% lower boundary Ub=ub.*ones(1,dim);% upper boundaryit=1;%Number of iterationsConvergence_curve=zeros(1,Max_iter);Rime_rates=zeros(1,N);%Initialize the fitness valuenewRime_rates=zeros(1,N);W = 5;%Soft-rime parameters, discussed in subsection 4.3.1 of the paper%Calculate the fitness value of the initial positionfor i=1:NRime_rates(1,i)=fobj(Rimepop(i,:));%Calculate the fitness value for each search agent%Make greedy selectionsif Rime_rates(1,i)<Best_rime_rateBest_rime_rate=Rime_rates(1,i);Best_rime=Rimepop(i,:);endend% Main loopwhile it <= Max_iterRimeFactor = (rand-0.5)*2*cos((pi*it/(Max_iter/10)))*(1-round(it*W/Max_iter)/W);%Parameters of Eq.(3),(4),(5)E =(it/Max_iter)^0.5;%Eq.(6)newRimepop = Rimepop;%Recording new populationsnormalized_rime_rates=normr(Rime_rates);%Parameters of Eq.(7)for i=1:Nfor j=1:dim%Soft-rime search strategyr1=rand();if r1< EnewRimepop(i,j)=Best_rime(1,j)+RimeFactor*((Ub(j)-Lb(j))*rand+Lb(j));%Eq.(3)end%Hard-rime puncture mechanismr2=rand();if r2<normalized_rime_rates(i)newRimepop(i,j)=Best_rime(1,j);%Eq.(7)endendendfor i=1:N%Boundary absorptionFlag4ub=newRimepop(i,:)>ub;Flag4lb=newRimepop(i,:)<lb;newRimepop(i,:)=(newRimepop(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;newRime_rates(1,i)=fobj(newRimepop(i,:));%Positive greedy selection mechanismif newRime_rates(1,i)<Rime_rates(1,i)Rime_rates(1,i) = newRime_rates(1,i);Rimepop(i,:) = newRimepop(i,:);if newRime_rates(1,i)< Best_rime_rateBest_rime_rate=Rime_rates(1,i);Best_rime=Rimepop(i,:);endendendConvergence_curve(it)=Best_rime_rate;it=it+1;endendfunction X=initialization(N,Dim,UB,LB)B_no= size(UB,2); % numnber of boundariesif B_no==1X=rand(N,Dim).*(UB-LB)+LB;end% If each variable has a different lb and ubif B_no>1for i=1:DimUb_i=UB(i);Lb_i=LB(i);X(:,i)=rand(N,1).*(Ub_i-Lb_i)+Lb_i;endend
end

Su, H., Zhao, D., Heidari, A. A., Liu, L., Zhang, X., Mafarja, M., & Chen, H. (2023). RIME: A physics-based optimization. Neurocomputing, 532, 183–214.https://doi.org/10.1016/j.neucom.2023.02.010