java 代码查重(三)常见的距离算法和相似度(相关系数)计算方法
目录
一、几种距离度量方法
【 海明距离 /汉明距离】
【 欧几里得距离(Euclidean Distance) 】
【 曼哈顿距离 】
【 切比雪夫距离 】
【 马氏距离 】
二、相似度算法
【 余弦相似度 】
【 皮尔森相关系数 】
【 Jaccard相似系数 /杰卡德距离】
【 Tanimoto系数 】
【点积相似度】
总结
一、几种距离度量方法
注: 机器学习中常用的几种距离度量方法
【 海明距离 /汉明距离】
海明距离用于衡量两个等长向量之间的差异。测量两个等长字符串之间不同字符的数量

注意:
基于编辑的距离测量中, 包括:
✔️汉明距离(测量两个等长字符串之间不同字符的数量);
✔️编辑距离(根据将一个字符串转换为另一个字符串需要多少次更正来计算。允许的更正包括插入、删除和替换。)
【 欧几里得距离(Euclidean Distance) 】
欧氏距离,测量欧几里得空间中两点间的直线距离,在机器学习和数据挖掘中被广泛使用。特别是在m维空间中,它能够准确地衡量两点之间的真实距离。
【 曼哈顿距离 】
曼哈顿距离,顾名思义,描述的是在标准坐标系中,两点沿各坐标轴移动的距离之和。它就像象棋中的“車”那样,只能沿着横轴或纵轴进行移动,所经过的距离即为曼哈顿距离。这种距离度量方式在几何学和机器学习等领域有着广泛的应用。


【 切比雪夫距离 】
切比雪夫距离是指向量空间中各维度上最大差值的度量。这种距离在某些领域具有其独特的应用价值,特别是在处理需要考虑最大差异的场景。

【 马氏距离 】
马氏距离,作为一种衡量点与分布之间距离的方法,能够有效地计算两个未知样本集的相似度。它充分考虑了各种特性之间的内在联系,并具有尺度无关性,即不受测量尺度的影响。
二、相似度算法
【 余弦相似度 】
余弦相似度通过向量夹角的余弦值衡量个体差异,其范围从-1到1,在处理文本、图像等数据时非常有用。

【 皮尔森相关系数 】
皮尔逊相关系数是一种用于度量两个变量的线性相关性的指标。取值范围为 -1 到 1。
1 表示完全正相关,-1 表示完全负相关,0 表示无相关性。
与余弦相似性计算类似,它通过计算两个集合的交集大小与集合大小的几何平均值之比来得出结果,在多个领域都有广泛的应用。

【 Jaccard相似系数 /杰卡德距离】
Jaccard系数通过交集与并集的比例衡量样本相似度,在处理0和1的向量时表现出色,计算效率高。适用于集合相似性度量,字符串相似性度量 。它受数据大小影响较大,常用于协同过滤等场景。
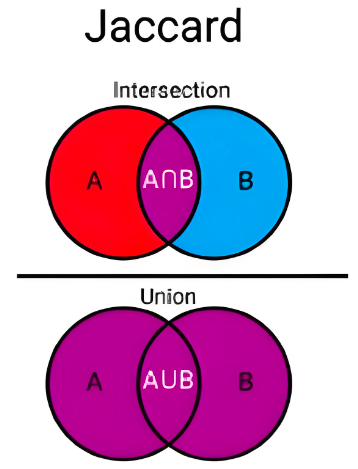
由Jaccard相似度,可以转换成Jaccard距离: Jaccard Distance(A, B) = 1 - Jaccard(A, B)
举例:
句子A:请问苹果电脑的价格
句子B:问下联想笔记本多少钱
分词提取特征:
SetA={请问,问苹,苹果,果电,电脑,脑的,的价,价格}
SetB={问下,下联,联想,想笔,笔记,记本,本多, 多少,少钱}
两个集合求交集得出相同语言片段个数为:0
两个集合求并集得出分母大小为:16
所以这两个句子的相似度为: 0/16=0
【 Tanimoto系数 】
Tanimoto系数,也被称为广义Jaccard相似系数,是用于向量相似性度量的一种方法,它与cosine相似度类似。
【点积相似度】
点积相似度是指:通过将两个向量的对应分量相乘后,将每个计算值相加求和得出结果,从而进行相似度检验。向量a和b的点积计算公式如下:

向量的点积也可以表示为向量的模与它们之间夹角余弦值的乘积:

总结
评估两个向量的相似程度有多种指标(Metrics):
- 欧式距离(Euclidean Distance) -- 考虑的向量属性:幅度和方向
- 余弦相似度(Cosine Similarity) -- 考虑的向量属性:只有方向
- 点积相似度(Dot product similarity) -- 考虑的向量属性:幅度和方向
当两用户评分趋势一致时,但是评分值差距很大,余弦相似度倾向给出更优解。例如向量(3,3)和(5,5),这两位用户的认知其实是一样的,但是欧式距离给出的解显然没有余弦值合理。
