支持向量机(SVM):分类与回归的数学之美
在机器学习的世界里,支持向量机(Support Vector Machine,简称 SVM)是一种极具魅力且应用广泛的算法。它不仅能有效解决分类问题,在回归任务中也有着出色的表现。下面,就让我们深入探索 SVM 如何在分类和回归问题中发挥作用。
一、SVM 概述
支持向量机由 Vapnik 等人于 1995 年正式提出,它基于统计学习理论,旨在寻找一个最优超平面,将不同类别的数据尽可能分开。SVM 的核心思想可以用 “间隔最大化” 来概括,通过找到一个能使两类数据点到超平面的最小距离最大的超平面,实现对数据的分类和回归预测。
二、SVM 用于分类问题
1. 线性可分情况
在最简单的线性可分情况下,假设有两类数据点,SVM 的目标是找到一个超平面 ,使得两类数据点能够被完全分开,并且两类数据点中离超平面最近的点到超平面的距离(称为间隔)最大。这些离超平面最近的点被称为支持向量。
数学上,间隔可以表示为,为了最大化间隔,SVM 通过求解以下优化问题:

其中,是第 i 个数据点的特征向量,
是其对应的类别标签
,n 是数据点的总数。通过求解这个优化问题,我们可以得到最优的 w 和 b,从而确定分类超平面。
2. 线性不可分情况
现实中的数据往往不是线性可分的,这时 SVM 引入了松弛变量来允许一些数据点错误分类或位于间隔内。优化问题变为:

这里的 C 是一个超参数,用于平衡间隔最大化和分类错误的容忍度。C 越大,对错误分类的惩罚越大,模型越倾向于严格分类;C 越小,模型对错误的容忍度越高,间隔可能会更大。
3. 非线性分类
对于非线性可分的数据,SVM 使用核函数(Kernel Function)将数据映射到高维空间,使得在高维空间中数据变得线性可分。常见的核函数有多项式核函数、高斯径向基函数(RBF)、Sigmoid 核函数等。以高斯 RBF 核函数为例,它的表达式为 。通过核函数,SVM 在低维空间中进行计算,却能在高维空间中找到合适的超平面进行分类。
三、SVM 用于回归问题
支持向量回归(Support Vector Regression,简称 SVR)是 SVM 在回归问题中的应用。与分类问题不同,SVR 的目标是找到一个函数 ,使得预测值与真实值之间的误差尽可能小。
SVR 引入了一个不敏感损失函数,即只要预测值与真实值之间的误差在
范围内,就认为误差为 0。SVR 的优化问题可以表示为:
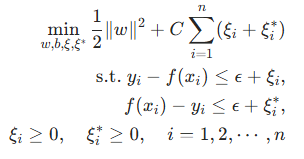
其中,和
分别表示预测值大于和小于真实值时的松弛变量,同样,C 是用于平衡模型复杂度和回归误差的超参数。
和分类类似,对于非线性回归问题,SVR 也可以使用核函数将数据映射到高维空间进行处理。
四、SVM 的优缺点
优点
- 泛化能力强:通过间隔最大化和核函数的使用,SVM 在小样本数据集上也能有较好的泛化性能。
- 适合高维数据:尤其是使用核函数时,能有效处理高维甚至无穷维的数据。
- 可解释性:分类超平面和支持向量直观地展示了模型的决策边界,有一定的可解释性。
缺点
- 计算复杂度高:在训练过程中,尤其是处理大规模数据集时,SVM 的计算量和内存需求较大。
- 超参数选择困难:超参数 C 和核函数的参数对模型性能影响很大,需要通过交叉验证等方法仔细调整。
- 对数据分布敏感:数据的分布情况可能会影响 SVM 的性能,例如数据不平衡时,SVM 的分类效果可能不理想。
五、SVM 的应用场景
SVM 在多个领域都有广泛的应用,在图像识别中,用于对图像中的物体进行分类;在文本分类中,帮助将文本划分到不同的主题类别;在生物信息学中,用于基因序列分类和蛋白质结构预测;在回归问题上,SVM 可用于预测房价、股票价格等连续值数据。
支持向量机凭借其独特的数学原理和强大的功能,在机器学习领域占据着重要的地位。无论是分类还是回归任务,SVM 都为我们提供了一种有效的解决方案。随着技术的不断发展,SVM 也在与其他算法结合,不断拓展其应用边界,为解决更多复杂的实际问题贡献力量。
