当前位置：首页 > news >正文

《深度学习入门》第2章感知机

news 来源：原创 2025/5/23 13:57:14

2.1 什么是感知机

在这里插入图片描述

2.2 简单逻辑电路

或门，与门，与非门等。

2.3 感知机的实现

2.3.1 简单的实现

用python实现与门

def AND(x, y):w1, w2, theta = 0.5, 0.5, 0.7tmp = x*w1 + y*w2if tmp <= theta:return 0else:return 1print(AND(1,0))
print(AND(1,1))
print(AND(0,0))

在这里插入图片描述

2.3.2 导入权重和偏置

在这里插入图片描述

2.1 公式中，将 θ 变为 -b 后，移到等号左端，变为偏置值。接下来只需要判断是否大于0。

import numpy as np
x = np.array([0, 1])     # 输入 x
w = np.array([0.5, 0.5]) # 权重 w
b = -0.7                 # 偏置 bprint(x * w)         # x 与 w 对应项相乘
print(sum(x * w))    # x 与 w 对应项相乘后求和
print(sum(x * w) + b)# x 与 w 对应项相乘后求和，再加偏置值

在这里插入图片描述

2.3.3 使用权重和偏置的实现

1.与门

# 与门
import numpy as npdef AND(x1, x2):x = np.array([x1, x2])     # 输入w = np.array([0.5, 0.5]) # 权重b = -0.7                 # 偏置tmp = sum(x * w) + bif tmp <= 0:return 0else:return 1print(AND(0, 0))
print(AND(0, 1))
print(AND(1, 0))
print(AND(1, 1))

在这里插入图片描述

2.与非门

# 与非门
import numpy as npdef NAND(x1, x2):x = np.array([x1, x2])     # 输入w = np.array([-0.5, -0.5]) # 修改b = 0.7                 # 修改tmp = sum(x * w) + bif tmp <= 0:return 0else:return 1print(NAND(0, 0))
print(NAND(0, 1))
print(NAND(1, 0))
print(NAND(1, 1))

在这里插入图片描述

3.或门

在这里插入图片描述

# 或门
import numpy as npdef OR(x1, x2):x = np.array([x1, x2])     # 输入w = np.array([0.5, 0.5]) # 权重b = -0.4                 # 偏置tmp = sum(x * w) + bif tmp <= 0:return 0else:return 1print(OR(0, 0))
print(OR(0, 1))
print(OR(1, 0))
print(OR(1, 1))

在这里插入图片描述

2.4 感知机的局限性

2.4.1 异或门

在这里插入图片描述

无法通过前面的感知机来实现异或门。

2.4.2 线性和非线性

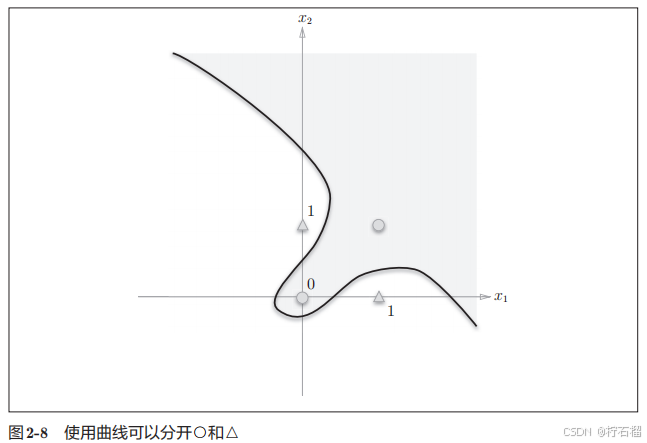
在这里插入图片描述

可以通过非线性的方式分隔开。

2.5多层感知机

2.5.1 已有门电路的组合

在这里插入图片描述

通过三个门组合可以组成异或门。

2.5.2 异或门的实现

import numpy as np
# 与门
def AND(x1, x2):x = np.array([x1, x2])     # 输入w = np.array([0.5, 0.5]) # 权重b = -0.7                 # 偏置tmp = sum(x * w) + bif tmp <= 0:return 0else:return 1# 与非门
def NAND(x1, x2):x = np.array([x1, x2])     # 输入w = np.array([-0.5, -0.5]) # 权重b = 0.7                 # 偏置tmp = sum(x * w) + bif tmp <= 0:return 0else:return 1 # 或门
def OR(x1, x2):x = np.array([x1, x2])     # 输入w = np.array([0.5, 0.5]) # 权重b = -0.4                 # 偏置tmp = sum(x * w) + bif tmp <= 0:return 0else:return 1# 异或门    
def XOR(x1, x2):s1 = NAND(x1, x2)s2 = OR(x1, x2)y = AND(s1, s2)return yprint(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))