Paillier加密方案的原理、实现与应用（vs）

一、实验目的

1、掌握NTL的基本配置和方法（以下是以visualstudio为例）

2、掌握Paillier加密方案的原理与实现

①钥匙生成：首先，生成一把钥匙，包括钥匙和私钥匙。钥匙由两个大素数(p,q)的乘积n和一个整数g组成，私钥匙由这两个大素数组成。

②加密过程：将明文m加密为密文c。加密时使用峰值n和g，以及一个随机数r。加密计算公式为c = E(m,r) = gmrn mod n2，其中m为明文，r为随机数。

③解密过程：利用私钥中的素数p和q，以及密文c进行解密。解密计算公式为[m = m = D(c,lambda) = (L(clambda mod n2) / L（glambda mod n2)) mod n，其中lambda = text{lcm}(p-1, q-1))，mu是模逆，L（u） = （u-1）/ n.

 二、实验设计

通过网盘分享的文件：WinNTL-11_5_0
链接: https://pan.baidu.com/s/1rkG9reIxSoJcbuyuEDWJGw?pwd=a898 提取码: a898 
--来自百度网盘超级会员v5的分享

1. 关于NTL的基本配置方法：

①在官网Download NTL (libntl.org)下载NTL的压缩文件，选择11.5.0如下：

②打开visualstudio，创建静态库的新项目，命名为NTL，如下：

③创建好项目后，右键NTL——>添加——>现有项会跳出文件窗口，过程如下：

④选择WinNTL-11_5_0\src下全部源文件（快捷方法直接ctrl+a选中全部，点击添加即可），如下：

⑥添加后得到环境如下：

⑦仍然是右键点击NTL，然后选择属性，在c/c++那一栏的常规选择附加包含目录如下：

⑧找到WinNTL-11_5_0下include文件夹的路径复制并粘贴到附件包含目录，并选择从父级或项目默认设置继承，如下：

⑨将SDL检查改为：否。如下：

⑩预编译头改为：不使用编译头。如下：

⑪右键项目--->生成，发现项目运行成功。如下：

查看项目文件，NTL--->Debug下，存在NTL.lib文件，说明项目WINNTL静态链接库创建成功

1. 进行检测：

①创建一个常规的项目，命名为test，如下：

②在WinNTL-11_3_4下include中的test里面找到quicktest，复制其代码放在刚创建好，并按上面配置好环境，如下：

③像前面NTL项目一样添加src部分的代码，配置c/c++常规部分，右键项目生成，发现代码运行成功，即检测完成。

1. Paillier加密方案代码的实现：

①除了添加src部分的代码，已经配置c/c++常规部分，仍然是右键项目，打开属性，找到连接器部分选择链接器--->常规--->附加库目录，选择NTL.lib文件所在的路径（NTL.lib是前面第一次编译后生成的文件），复制粘贴在附加库目录里面，如下：

②再选择输入--->附加依赖项，加上NTL.lib，选择确定。如下：

③在项目中写入Paillier加密的代码运行实现得到结果。如下：

三、实验记录

1、操作实验结果截屏如下：

其中p，q是随机生成的两个大质数，n=p*q，lambda=（p-1）*（q-1），m是明文，c是密文，

m2是生成的密文后，密文解密后得到的，经程序比对，m2=m,则解密成功

2、遇到的问题：

①：在第一遍NTL配置好环境后，检验测试时，新建的项目，复制粘贴在环境后直接运行生成，忘记了添加WinNTL-11_5_0下include中的src，导致出现错误提示如下：

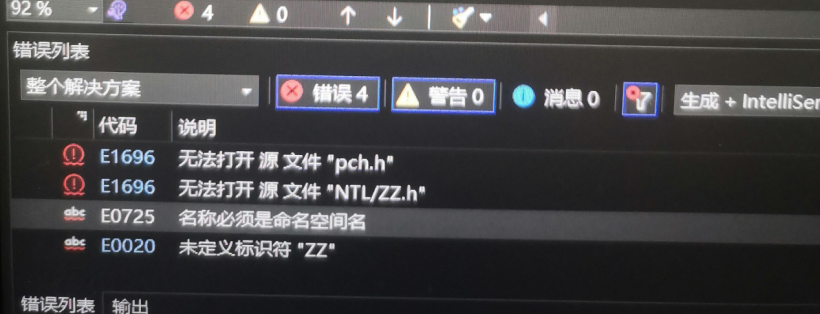
后来发现经及时修改后代码正常运行。

②出现了“一元负运算符应用于无符号类型，结果仍为无符号类型”的错误，如下：

经百度后，发现右键项目--->属性--->配置属性--->C/C++--->常规--->SDL检查，设置为否，则可运行成功。

四、实验思考或体会

在此次实验中我并没有使用dev实现Paillier算法，而是选择了visualstudio，是因为版本问题，让我始终无法自动生成NTL.a的文件，于是通过百度选择用visualstudio实现Paillier算法算法，完成此次实验，并发现visualstudio相比dev实验更简洁。

通过实验，我理解了Paillier算法的原理，并设计了用C++高级程序语言实现Paillier算法的加解密。

首先，设计一个Paillier类，将成员类型设置为NTL库里的ZZ大整数类型，以防溢出；

然后对主要的生成素数对p,q，按照加密解密公式c = E(m,r) = gmrn mod n2/m = D(c,lambda) = (L(clambda mod n2) / L（glambda mod n2)) mod n，写出c++程序，对加密和解密等函数进行实现

最后掌握了Paillier算法在C++上的实现。