当前位置：首页 > news >正文

【漫话机器学习系列】270.KNN算法（K-Nearest Neighbors）

news 来源：原创 2025/5/21 9:37:02

【图文详解】KNN算法原理与可视化讲解

一、KNN算法简介

KNN（k-nearest neighbors，k近邻算法）是一种基本且常用的监督学习算法，广泛应用于分类与回归问题中。KNN的思想非常直观：一个样本的分类结果由其周围的K个最近邻样本的类别决定。

在分类任务中，KNN 不依赖显式的模型拟合过程，而是基于距离度量、进行多数投票的懒惰学习算法。

二、KNN算法的原理要点

以下是通过手绘图呈现的 KNN 算法关键点总结（图源如图）：

K 值的含义

K 值代表参与分类的“邻近单元”数量，即用来决定目标类别的最近邻数量。
K 的选择非常关键：太小会受噪声影响，太大可能引入过多无关数据。

K 值的选择技巧

K 一般取奇数，避免在二分类问题中出现平票（tie）。
可以通过交叉验证（cross-validation）方式来选取最优的 K 值。

特征处理

如果特征中包含二进制特征（如0/1，True/False），可以使用海明距离（Hamming Distance）进行计算。
若特征为数值型，则使用欧氏距离最为常见。

分类逻辑

待分类样本会与所有训练样本计算距离；
取前 K 个距离最小的样本；
根据这 K 个样本的类别进行“投票”，多数类别即为预测类别；
有时也会加入距离加权投票，越近的邻居权重越高。

KNN 的劣势

不适用于大规模数据：计算每个样本距离代价高，且无法预训练；
特征维度高时性能降低：受“维度灾难”影响，距离的判别能力减弱。

三、手绘图示讲解

下面我们结合手绘图来说明 KNN 的实际分类过程。

场景说明：

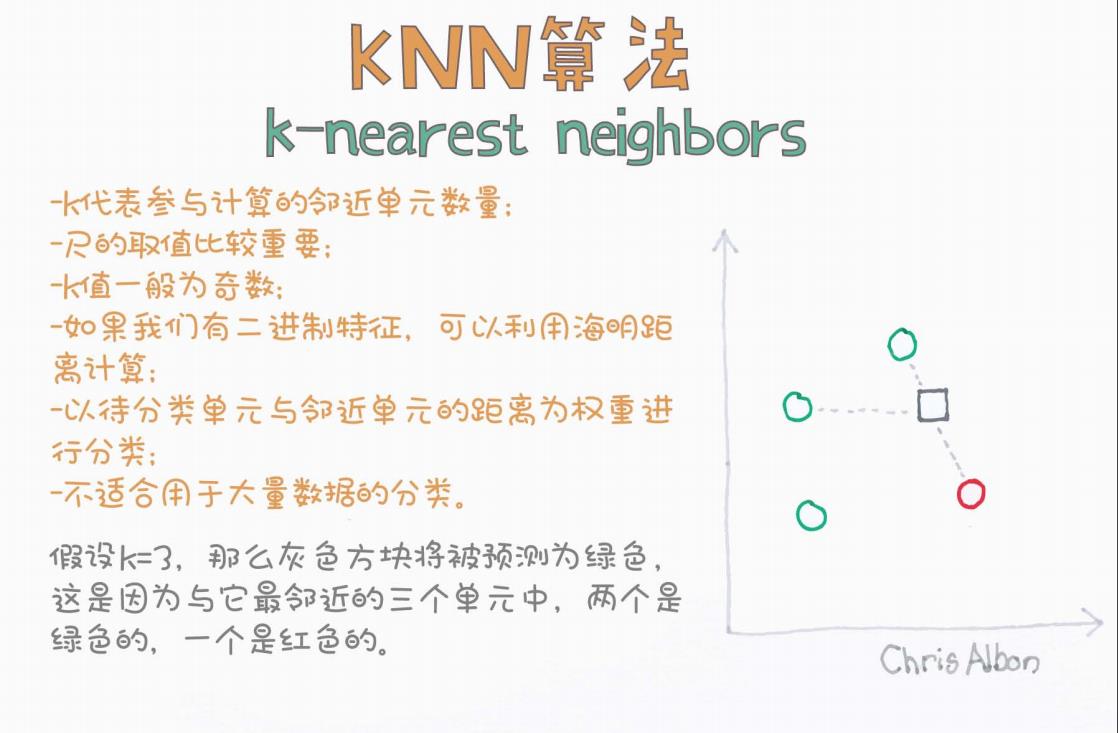
图中显示了若干训练样本点（绿色圆圈与红色圆圈），其中绿色代表某一类别，红色代表另一类别；
灰色方块表示一个待分类的样本点；
灰色虚线连接的是该样本与最近的三个邻居。

举例说明（设 K=3）：

灰色方块与其最近的 3 个邻居如下：
- 绿色圆圈 × 2
- 红色圆圈 × 1
由于绿色类别占多数（2 > 1），灰色方块最终被判定为绿色类别。

这就是 KNN 算法中最基本的“多数投票”原则的体现。

四、距离的选择

KNN 的核心在于“距离”的计算，常见的距离计算方式包括：

距离类型	公式	适用场景
欧氏距离		连续数值特征
曼哈顿距离	$d=\sum_{i=1}^{n}$	$x_i-y_i$
闵可夫斯基距离	泛化公式，可调参数 p 控制
海明距离	适用于离散/二值特征

不同的场景应选用合适的距离度量方式，以提升分类效果。

五、KNN 的应用场景

KNN 在以下场景中非常实用：

图像识别（如手写数字识别）
推荐系统
信用卡欺诈检测
医学诊断
文本分类

但在处理超大数据或高维数据时，建议结合降维（如 PCA）或使用更高效的近似算法（如 KD 树、Ball 树、Annoy 等）。

六、总结与建议

KNN 是一种入门级但非常直观的算法，适合用来理解机器学习中的“相似性”和“邻近性”思想。尽管它计算成本高、对数据规模和维度敏感，但在小样本、低维场景下，仍是一种简单高效的分类方法。

建议初学者可以通过以下方式进一步学习：

用 sklearn 实现 KNN 并进行实战训练
尝试不同距离度量方式和 K 值比较效果
将 KNN 应用于实际数据集（如 Iris、MNIST）

附：KNN 实现推荐

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加载数据
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3)# 创建模型
model = KNeighborsClassifier(n_neighbors=3)
model.fit(X_train, y_train)# 预测与评估
print(model.score(X_test, y_test))

欢迎收藏、点赞并关注我，后续将推出更多算法可视化解读系列内容。
如有问题或建议，欢迎评论区交流！