AI大模型应对挑战，使用winform实现小球在旋转五边形内的舞蹈

前言

欢迎关注dotnet研习社，最近看到这样的一些博客"AI大模型应对挑战"
结合这些博客的思路，开发了一个这样的物理模拟程序。

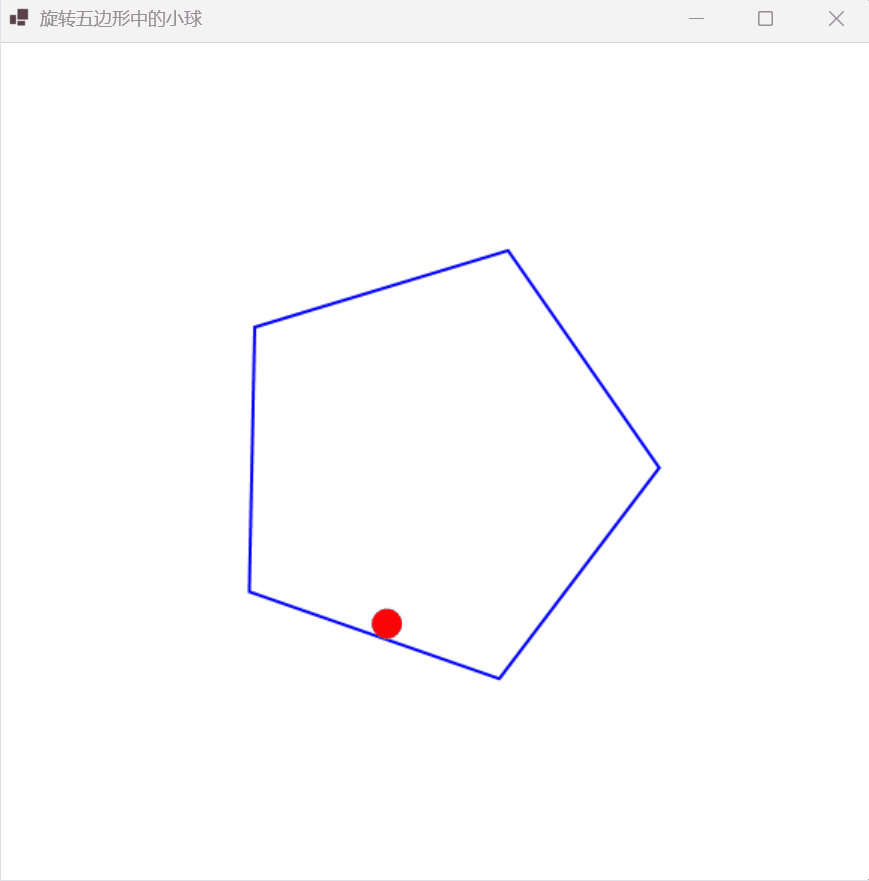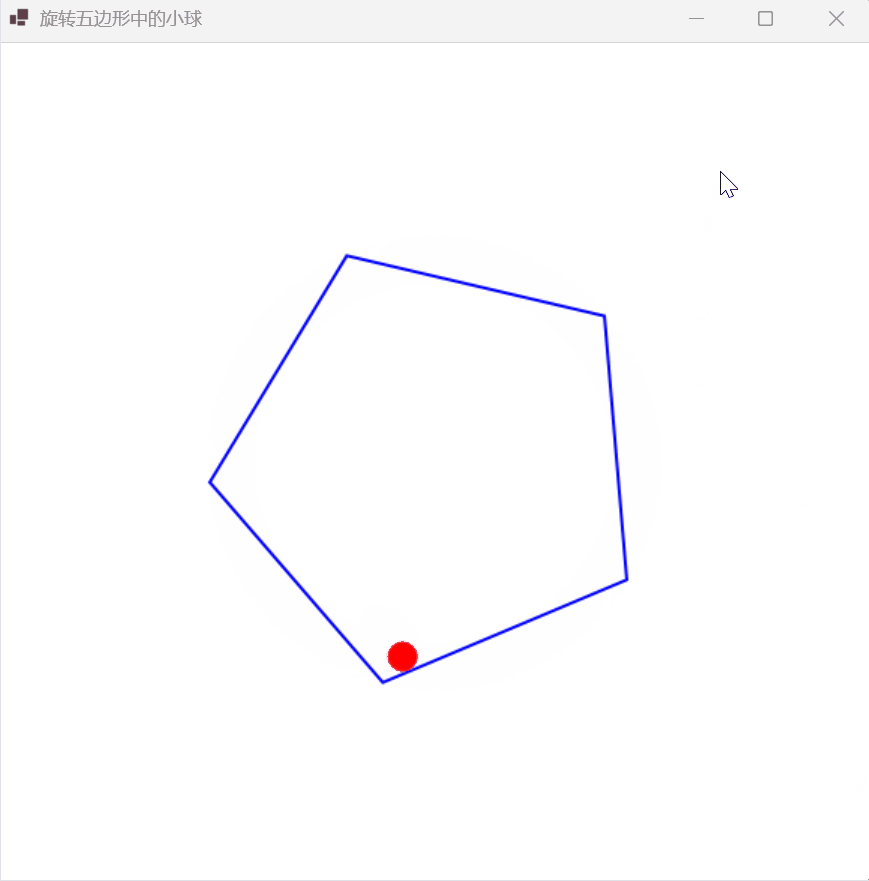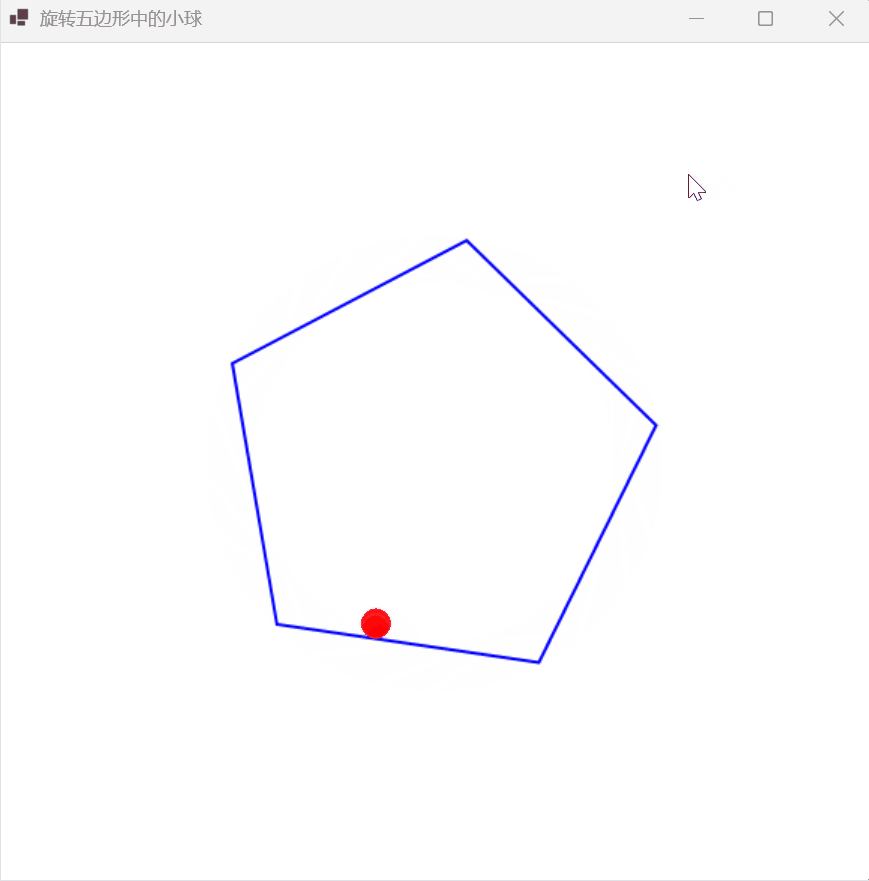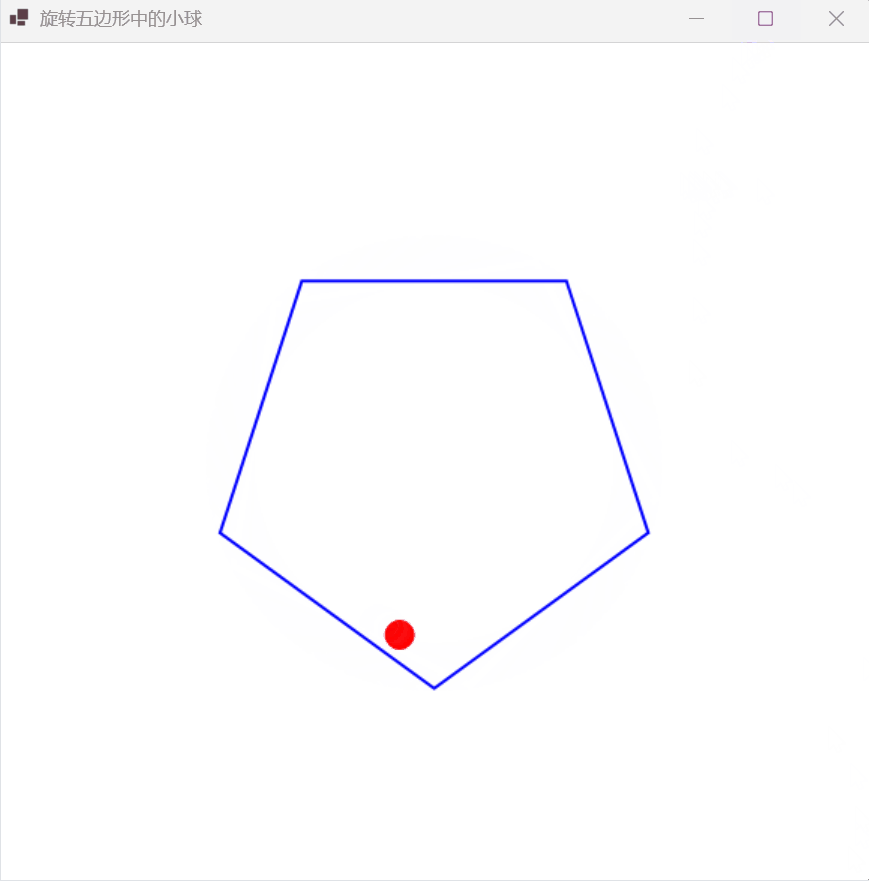
我将详细介绍如何使用 WinForm开发一个物理模拟程序，实现一个红色小球在顺时针旋转的五边形内部遵循重力规律运动的效果。这个项目不仅展示了基本的图形绘制技术，还涉及到物理碰撞检测和反弹计算等内容。学习游戏物理和图形编程的良好起点，可以作为更复杂模拟的基础。

项目需求

我们的任务是创建一个动画模拟，具体要求如下：

• 创建一个顺时针旋转的五边形
• 在五边形内添加一个红色小球
• 小球需要遵循重力规律在五边形内晃动
• 小球与五边形边界碰撞时需要正确反弹
• 确保小球不会飞出五边形
• 整个动画需要流畅

项目结构

项目由以下几个主要文件组成：

1. Program.cs - 程序入口点
2. Form1.cs - 主窗体代码，包含所有的物理模拟和绘图逻辑
3. Form1.Designer.cs - 窗体设计器生成的代码
4. RotatingPentagon.csproj - 项目文件

开发环境

• 开发语言：C#
• 框架：.NET 8.0
• 开发工具：Visual Studio 2022
• 目标平台：Windows

实现过程

1. 创建项目

首先，我们创建了一个基于.NET 8.0的WinForm应用程序。项目文件RotatingPentagon.csproj如下：

<Project Sdk="Microsoft.NET.Sdk"><PropertyGroup><OutputType>WinExe</OutputType><TargetFramework>net8.0-windows</TargetFramework><UseWindowsForms>true</UseWindowsForms><ImplicitUsings>enable</ImplicitUsings></PropertyGroup></Project>

这是一个现代化的SDK风格项目文件，指定了输出类型为Windows可执行文件，目标框架为.NET 8.0-windows，并启用了Windows Forms支持。

2. 程序入口点

Program.cs文件包含程序的入口点，负责初始化应用程序并启动主窗体：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Threading.Tasks;
using System.Windows.Forms;namespace RotatingPentagon
{static class Program{/// <summary>/// 应用程序的主入口点。/// </summary>[STAThread]static void Main(){Application.EnableVisualStyles();Application.SetCompatibleTextRenderingDefault(false);Application.Run(new Form1());}}
}

3. 主窗体设计

Form1.Designer.cs文件包含窗体的设计器生成代码，主要负责初始化窗体组件：

namespace RotatingPentagon
{partial class Form1{/// <summary>/// 必需的设计器变量。/// </summary>private System.ComponentModel.IContainer components = null;/// <summary>/// 清理所有正在使用的资源。/// </summary>/// <param name="disposing">如果应释放托管资源，为 true；否则为 false。</param>protected override void Dispose(bool disposing){if (disposing && (components != null)){components.Dispose();}base.Dispose(disposing);}#region Windows 窗体设计器生成的代码/// <summary>/// 设计器支持所需的方法 - 不要修改/// 使用代码编辑器修改此方法的内容。/// </summary>private void InitializeComponent(){this.components = new System.ComponentModel.Container();this.AutoScaleMode = System.Windows.Forms.AutoScaleMode.Font;this.ClientSize = new System.Drawing.Size(800, 450);this.Text = "Form1";}#endregion}
}

4. 核心实现 - Form1.cs

Form1.cs是项目的核心，包含了所有的物理模拟和绘图逻辑。下面我将分模块详细讲解：

4.1 基本属性和初始化

首先，我们首先定义了一些关键参数：

• 五边形的大小、角度和旋转速度
• 小球的位置、速度、大小和物理特性
• 用于动画更新的定时器

// 五边形的参数
private float pentagonRadius = 150;
private float pentagonAngle = 0;
private float pentagonRotationSpeed = 0.02f;
private PointF pentagonCenter;
private PointF[] pentagonPoints = new PointF[5];// 小球的参数
private PointF ballPosition;
private PointF ballVelocity;
private float ballRadius = 10;
private float gravity = 0.2f;
private float bounceFactor = 0.8f;// 定时器
private System.Windows.Forms.Timer animationTimer;

在构造函数中，我们初始化窗体和各个组件：

• 启用了双缓冲以减少闪烁
• 设置了窗体的背景色、大小和标题
• 将五边形放置在窗体中心
• 初始化小球的位置和速度
• 创建并启动了一个定时器，用于更新动画

public Form1()
{InitializeComponent();this.DoubleBuffered = true;  // 启用双缓冲，减少闪烁this.BackColor = Color.White;this.Size = new Size(600, 600);this.Text = "旋转五边形中的小球";// 初始化五边形中心点pentagonCenter = new PointF(this.ClientSize.Width / 2, this.ClientSize.Height / 2);// 初始化小球位置和速度ballPosition = new PointF(pentagonCenter.X, pentagonCenter.Y - pentagonRadius / 2);ballVelocity = new PointF(1.0f, 0.0f);// 设置定时器animationTimer = new System.Windows.Forms.Timer();animationTimer.Interval = 5; // 约200帧每秒animationTimer.Tick += AnimationTimer_Tick;animationTimer.Start();
}

4.2 动画更新

定时器的Tick事件处理程序负责更新模拟状态：
每次定时器触发时，我们需要：

1. 更新五边形的旋转角度
2. 重新计算五边形的顶点位置
3. 更新小球的位置
4. 请求窗体重绘

private void AnimationTimer_Tick(object sender, EventArgs e)
{// 更新五边形旋转角度pentagonAngle += pentagonRotationSpeed;if (pentagonAngle > 2 * Math.PI)pentagonAngle -= (float)(2 * Math.PI);// 计算五边形的顶点CalculatePentagonPoints();// 更新小球位置UpdateBallPosition();// 重绘窗体this.Invalidate();
}

4.3 五边形顶点计算

根据旋转角度计算五边形的五个顶点位置：

private void CalculatePentagonPoints()
{for (int i = 0; i < 5; i++){float angle = pentagonAngle + (float)(i * 2 * Math.PI / 5);pentagonPoints[i] = new PointF(pentagonCenter.X + pentagonRadius * (float)Math.Cos(angle),pentagonCenter.Y + pentagonRadius * (float)Math.Sin(angle));}
}

4.4 小球位置更新与碰撞检测

小球的运动受重力影响，并且需要检测与五边形边界的碰撞：

private void UpdateBallPosition()
{// 应用重力ballVelocity.Y += gravity;// 更新位置ballPosition.X += ballVelocity.X;ballPosition.Y += ballVelocity.Y;// 检测与五边形边界的碰撞CheckCollisionWithPentagon();
}

每一帧，我们需要：

1. 给小球的Y方向速度增加重力加速度
2. 根据速度更新小球位置
3. 检查小球是否与五边形边界发生碰撞

碰撞检测是整个项目的核心部分，我们需要检查小球是否与五边形的任意一条边发生碰撞，如果发生碰撞，则计算反弹方向和速度：

• 遍历五边形的每条边
• 检查小球是否与边发生碰撞
• 如果发生碰撞，计算反弹方向和速度
• 应用能量损失系数，使小球逐渐减速
• 将小球推离边界，防止卡住
• 最后确保小球始终在五边形内部

private void CheckCollisionWithPentagon()
{for (int i = 0; i < 5; i++){int j = (i + 1) % 5;PointF p1 = pentagonPoints[i];PointF p2 = pentagonPoints[j];// 检查小球是否与边界碰撞if (IsCollisionWithLine(ballPosition, ballRadius, p1, p2, out PointF normal)){// 计算反弹float dot = ballVelocity.X * normal.X + ballVelocity.Y * normal.Y;// 反弹速度ballVelocity.X -= 2 * dot * normal.X;ballVelocity.Y -= 2 * dot * normal.Y;// 应用能量损失ballVelocity.X *= bounceFactor;ballVelocity.Y *= bounceFactor;// 将小球推出边界以防止卡住float overlap = ballRadius - DistancePointToLine(ballPosition, p1, p2);ballPosition.X += normal.X * overlap;ballPosition.Y += normal.Y * overlap;}}// 确保小球不会飞出五边形EnsureBallInsidePentagon();
}

4.5 碰撞检测算法

检测小球与线段的碰撞是一个关键算法：

1. 计算小球中心到线段的最短距离
2. 如果距离小于小球半径，则发生碰撞
3. 计算碰撞法线，用于后续的反弹计算

private bool IsCollisionWithLine(PointF ballPos, float radius, PointF lineStart, PointF lineEnd, out PointF normal)
{normal = new PointF(0, 0);// 计算线段向量float lineVectorX = lineEnd.X - lineStart.X;float lineVectorY = lineEnd.Y - lineStart.Y;// 计算小球到线段起点的向量float ballToLineStartX = ballPos.X - lineStart.X;float ballToLineStartY = ballPos.Y - lineStart.Y;// 计算线段长度的平方float lineLengthSquared = lineVectorX * lineVectorX + lineVectorY * lineVectorY;// 计算投影比例float t = Math.Max(0, Math.Min(1, (ballToLineStartX * lineVectorX + ballToLineStartY * lineVectorY) / lineLengthSquared));// 计算最近点float closestPointX = lineStart.X + t * lineVectorX;float closestPointY = lineStart.Y + t * lineVectorY;// 计算距离float distanceX = ballPos.X - closestPointX;float distanceY = ballPos.Y - closestPointY;float distanceSquared = distanceX * distanceX + distanceY * distanceY;// 检查是否碰撞if (distanceSquared <= radius * radius){// 计算法线float distance = (float)Math.Sqrt(distanceSquared);if (distance > 0){normal.X = distanceX / distance;normal.Y = distanceY / distance;}else{// 如果小球中心正好在线上，使用垂直于线段的向量作为法线normal.X = -lineVectorY / (float)Math.Sqrt(lineLengthSquared);normal.Y = lineVectorX / (float)Math.Sqrt(lineLengthSquared);}return true;}return false;
}

为了计算碰撞，我们需要一个辅助函数来计算点到线段的距离，这个函数计算点到线段的最短距离，用于确定碰撞深度。

private float DistancePointToLine(PointF point, PointF lineStart, PointF lineEnd)
{float lineVectorX = lineEnd.X - lineStart.X;float lineVectorY = lineEnd.Y - lineStart.Y;float pointToLineStartX = point.X - lineStart.X;float pointToLineStartY = point.Y - lineStart.Y;float lineLengthSquared = lineVectorX * lineVectorX + lineVectorY * lineVectorY;float t = Math.Max(0, Math.Min(1, (pointToLineStartX * lineVectorX + pointToLineStartY * lineVectorY) / lineLengthSquared));float closestPointX = lineStart.X + t * lineVectorX;float closestPointY = lineStart.Y + t * lineVectorY;float dx = point.X - closestPointX;float dy = point.Y - closestPointY;return (float)Math.Sqrt(dx * dx + dy * dy);
}

4.6 确保小球在五边形内部

为了防止小球飞出五边形，我们添加了一个安全检查，检查小球是否在五边形内部，如果不在则将其重置到中心位置：

private void EnsureBallInsidePentagon()
{// 检查小球是否在五边形内部if (!IsPointInPentagon(ballPosition)){// 如果不在内部，将小球放回五边形中心ballPosition = pentagonCenter;ballVelocity = new PointF(1.0f, 0.0f);}
}
//为了检测点是否在五边形内，我们使用了射线法：是一个经典的点在多边形内部检测算法，通过计算从点发出的射线与多边形边的交点数量来判断点是否在多边形内部。
private bool IsPointInPentagon(PointF point)
{bool inside = false;for (int i = 0, j = 4; i < 5; j = i++){if (((pentagonPoints[i].Y > point.Y) != (pentagonPoints[j].Y > point.Y)) &&(point.X < (pentagonPoints[j].X - pentagonPoints[i].X) * (point.Y - pentagonPoints[i].Y) / (pentagonPoints[j].Y - pentagonPoints[i].Y) + pentagonPoints[i].X)){inside = !inside;}}return inside;
}

4.7 绘制图形

重写OnPaint方法，绘制五边形和小球：我们使用GDI+绘制了蓝色的五边形和红色的小球，并启用了抗锯齿以获得更平滑的图形。

protected override void OnPaint(PaintEventArgs e)
{base.OnPaint(e);Graphics g = e.Graphics;g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;// 绘制五边形using (Pen pentagonPen = new Pen(Color.Blue, 2)){g.DrawPolygon(pentagonPen, pentagonPoints);}// 绘制小球using (SolidBrush ballBrush = new SolidBrush(Color.Red)){g.FillEllipse(ballBrush, ballPosition.X - ballRadius, ballPosition.Y - ballRadius, ballRadius * 2, ballRadius * 2);}
}

开发过程中遇到的问题及解决方案

1. 碰撞检测的精确性

实现精确的碰撞检测是一个挑战，特别是当五边形旋转时。我们使用了点到线段的最短距离来检测碰撞，并计算碰撞法线用于反弹。

2. 防止小球卡在边界

小球可能会卡在五边形的边界上，为了解决这个问题，我们在检测到碰撞后，将小球沿法线方向推出一定距离：

float overlap = ballRadius - DistancePointToLine(ballPosition, p1, p2);
ballPosition.X += normal.X * overlap;
ballPosition.Y += normal.Y * overlap;

3. 确保小球不会飞出五边形

我们实现了一个点在多边形内部的检测算法（射线法），用于确保小球始终在五边形内部。如果小球飞出五边形，我们将其重置到中心位置。

性能优化

为了确保动画流畅，我们采取了以下优化措施：

1. 启用双缓冲（this.DoubleBuffered = true），减少闪烁
2. 使用高效的碰撞检测算法
3. 优化绘图代码，使用AntiAlias模式提高图形质量

运行测试

总结

通过这个项目，我们实现了一个简单但有趣的物理模拟：一个红色小球在旋转的五边形内部遵循重力规律运动。这个项目涉及到了以下几个方面的知识：

1. WinForm图形绘制
2. 基本的物理模拟（重力、碰撞、反弹）
3. 几何算法（点到线段的距离、点在多边形内的判断）
4. 动画实现（使用Timer控制帧率）