力扣-盛最多水的容器
1.题目描述
2.题目链接
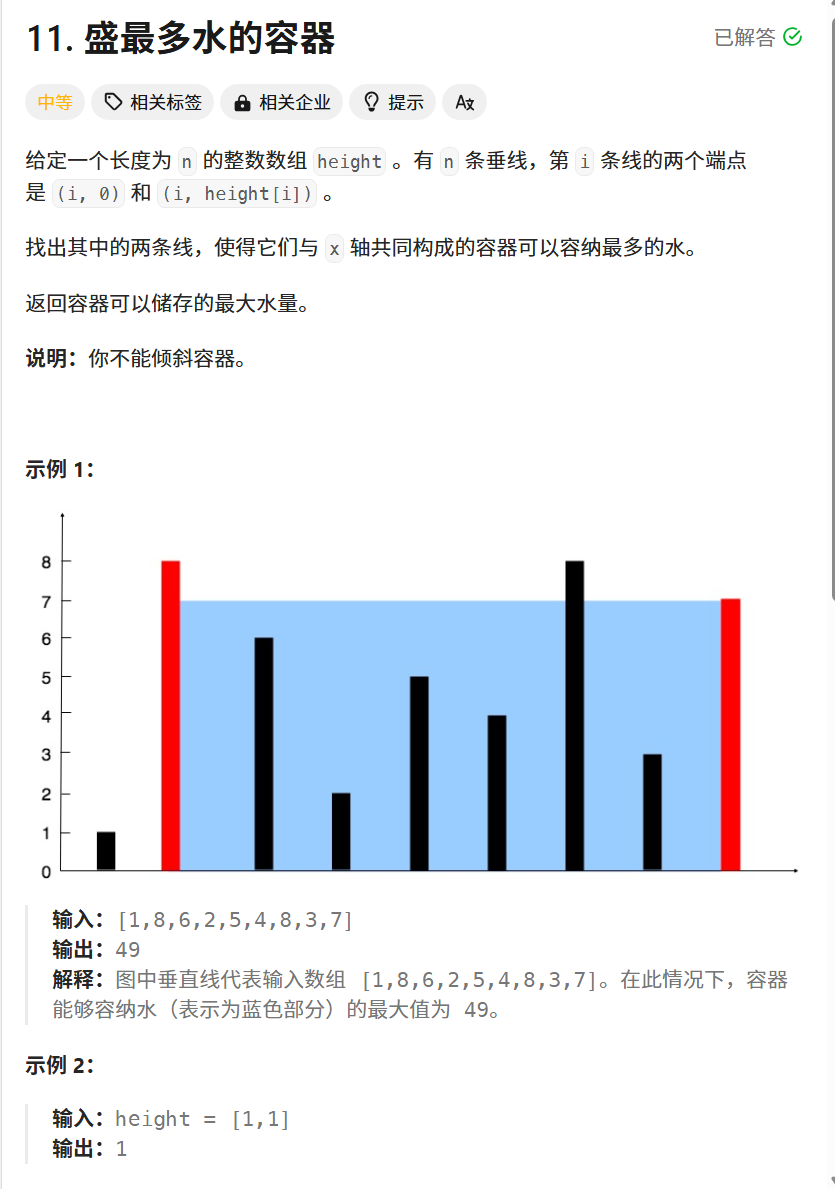
11. 盛最多水的容器 - 力扣(LeetCode)
3.题目解析
题目中的储水量=两边差*短边高度。也就是说,两条边中,决定储水量的是短边的高度。
我们可以定义两个指针,一个在最左边,一个在最右边。
那么双指针的移动逻辑是什么呢?
首先,无论是移动左指针,还是移动右指针,只要移动指针,两边差就都会缩小,而且缩小的幅度一样(都是走一步)。
第二,储水量=两边差*短边高度,如果我们移动较高边的指针,会有两种情况:
1.得到的新边curNew大于原较低边的高度dest,那么“储水量=两边差*短边高度”的中的短边高度就没有影响:min(height【curNew】,height【dest】)还是等于height【dest】,所以储水量计算公式中的短边高度依然是原来的height【dest】。而两边差是已知缩小的,所以储水量会变小。
2.得到的新边curNew小于原较低边的高度dest,那么“储水量=两边差*短边高度”的中的短边高度就会变小:min(height【curNew】,height【dest】)=height【curNew】且height【curNew】<height【dest】,也就是说,这种情况下,短边高度虽然受到影响,变为height【curNew】,但是新的短边高度height【curNew】<原来的短边高度height【dest】。两边差和短边高度都在变小,所以“储水量=两边差*短边高度”自然也就变小了。
这里我们用到了数学中的单调性判断,可以得到我们要想得到更高储水量,就只能移动较低边的指针。
我们可以不断地移动较低边的指针,并把每一个储水量V计算出来,再定义一个int型整数ret=0,不断地取ret和新储水量的最大值,当cur=dest时,双指针相遇,数组遍历完毕,我们也就得到储水量的最大值。
4.解答代码
class Solution {public int maxArea(int[] height) {int cur=0,dest=height.length-1,ret=0;while(cur<dest){int v=Math.min(height[cur],height[dest])*(dest-cur);ret=Math.max(ret,v);if(height[cur]<height[dest]){cur++;}else{dest--;}}return ret;}
}