排序复习/上(C语言版)
目录
1.排序概念
2.冒泡排序
效率性能测试代码:
性能分析:
3.直接插入排序
单趟:
整体:
性能分析:
4.希尔排序(基于插入排序的优化)
单趟单组:
单趟多组:
降低循环层次的办法:
整体:
性能分析:
5.选择排序
6.堆排序
1.排序概念
让所有数据从小到大/从大到小,就是排序的概念
常见的排序算法:
1.直接插入排序 2.希尔排序
3.选择排序 4.堆排序
5.冒泡排序 6.快速排序
7.归并排序
2.冒泡排序
效率性能测试代码:
void TestOP()
{srand(time(0));const int N = 50000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);int* a9 = (int*)malloc(sizeof(int) * N);int* a10 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){//重复数据多(函数特性,随机值范围在0~32767)a1[i] = rand();//重复数据不多//a1[i] = rand() + i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];a9[i] = a1[i];a10[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HPSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();int begin8 = clock();QuickSortNON(a8, 0, N - 1);int end8 = clock();int begin9 = clock();MergeSortNON(a9, N);int end9 = clock();int begin10 = clock();CountSort(a10, N);int end10 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("QuickSortNON:%d\n", end8 - begin8);printf("MergeSort:%d\n", end6 - begin6);printf("MergeSortNON:%d\n", end9 - begin9);printf("BubbleSort:%d\n", end7 - begin7);printf("CountSort:%d\n", end10 - begin10);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a8);free(a9);free(a10);
}int main()
{TestOP();return 0;
}rand()范围在0~32767,如果有32769个数据那么就肯定有至少一个数据是重复的
为了降低重复数量,因此可以+i 来优化
for (int j = 0;j < n;j++){//单趟for (int i = 0;i < n - j - 1;i++){if (a[i] > a[i + 1]) Swap(&a[i], &a[i + 1]);}}冒泡排序:前后比较往后交换,交换时可以把大的往后挪,因此每次交换完可以把一个位置的元素确定好位置
最开始的一次要冒泡到n-1位置,为防止越界需要考虑清楚循环推出条件;当 j = 0 时,n - 1 = i 的话会出现a[n]越界,因此循环退出条件还需要 - 1
优化:若[0,j]位置没有发生任何交换,说明已经有序了,直接停止循环
void BubbleSort(int* a, int n)
{for (int j = 0;j < n;j++){//单趟int flag = 1;for (int i = 0;i < n - j - 1;i++){if (a[i] > a[i + 1]) Swap(&a[i], &a[i + 1]);flag = 0;}if (flag) break;}}性能分析:
时间复杂度:
最坏:N^2
最好:N,数据已经有序
3.直接插入排序
概念:对一个数组[3,9,10,21,5,4],假设要升序排序;5往前移动,先和10、21比较,无法插入;再往前移动,和9、10比较,无法插入;再往前移动,和3、9比较,可以插入(斗地主整理手牌用到的就是插入排序的思想)
排序思想:以上图为例,先把end下标后面一个元素(假设为tmp)保存下来,然后依次比较end下标元素和tmp大小,如果不合适就把从end往后覆盖1位,直到tmp到了合适的位置,把保存下来的值覆盖原来end+1下标元素(这样end+1下标元素才不会在数组中重复两次)
整体逻辑:[0,end]排序完毕,[end+1,size] 需要排序,因此直接直接在数组中从头到尾对每个下标元素往前做一次插入排序,即能完成排序
极端情况:当tmp是整个数组最小的,此时end下标会变成-1,需要解决
在处理复杂函数时,我们可以先从单趟排序写起,然后拓展到整体排序
单趟:
int end;int temp = a[end + 1];while (end >= 0){if (temp < a[end]){a[end + 1] = a[end]; end--;}else break; }a[end + 1] = temp;假设[0,end]有序,end+1位置的值往前比较插入
为防止覆盖后,原值不在,因此需要有一个temp存储end+1位置的值"a[end + 1] = a[end];" 要想把数据往后挪,通过覆盖后一个值的方法
当temp比end下标值大,则比[0,end]位置的值都大;可以直接覆盖掉此时end+1下标位置的元素(因为已经将原来temp位置的元素已经覆盖掉了,[end+1,end+2]位置的元素相同了)
整体:
void InsertSort(int* a, int n)
{for (int i = 0;i < n - 1;i++){int end = i;int temp = a[end + 1];while (end >= 0){if (temp < a[end]){a[end + 1] = a[end]; end--;}else break; }a[end + 1] = temp;}
}对每个数进行一次插入排序,从[0,end]有序到[0,n]有序
只能遍历到n-2,temp = a[n] 会导致数组越界通过循环语句的推出条件,直接解决了极限情况;出现极限情况时end为-1,a[end+1] = a[0] = temp
性能分析:
时间复杂度:
最坏:N^2,逆序时是最坏情况(一次break语句都不会执行)
最好:N,顺序时是最好情况(每个temp进入循环就break)
为什么与冒泡排序时间复杂度相同,但实际运行起来插入排序快那么多?
首先,我们刚刚考虑的只是最好、最坏的情况,没有考虑普遍情况
对于插入排序,只要temp比[0,end]位置中的某一数据大时,就可以直接break;每一个数据往前排的时候大概率都能进行break,或多或少跳过了几个数据没有运行,积少成多,运行时间就大大缩减了
对于冒泡排序,只有[0,j]位置完全有序才能break,break的条件比较苛刻;同时,只有完全有序时才能停止循环,无法像插入排序那样积少成多
4.希尔排序(基于插入排序的优化)

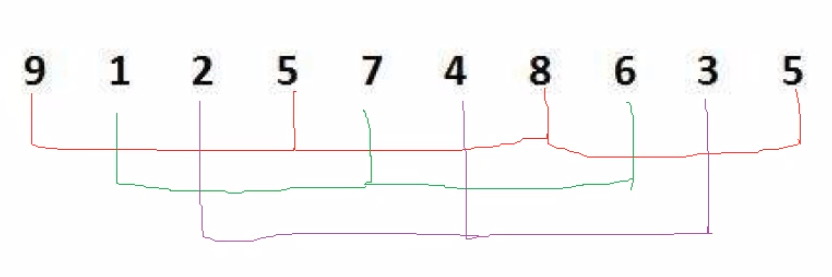
希尔排序:
1.预排序(让数据接近有序)
2.对已经预排序完的数组进行插入排序
插入排序的不足之处:每个数都有概率往前移动非常多次才能break;希尔排序就是基于插入排序优化,用来解决插入排序的这一不足
1.单组预排序
预排序的方法:将n个数分为gap组,两数间隔为gap的为一组(如上图),然后对每一组分别进行插入排序;此时假设有一个大的数在数组最后位置,(升序排序时)往前跳得比较快,能一次跳gap个数
把插入排序的 1 全部改成 gap 即可,因为是对两数相隔为gap的组进行插入排序(从相隔为1 -> 相隔为gap)
2.多组预排序
总共有分别以[0,gap-1]下标为开头元素的gap组,因此外面套一层[0,gap-1]的循环
3.整体排序:
gap == 1 时,相当于插入排序了;gap > 1 时,相当于预排序
因此我们可以使用这样的一个思想:用预排序组成整体排序
gap越大,每组中的元素跳得越快,数组越无序;gap越小,每组中的元素跳得越慢,数组越有序
gap怎么变化最好? 科学研究每次 gap/3 是最好的
gap = gap/3 ,假设gap为2时,最后结果为0,gap为0就不会对数组元素进行排序,因此需要在末尾 +1 来保证最小的gap值为1
单趟单组:
int gap = 3;//假设gap为3for (int i = 0;i < n - gap;i += gap) //为防止数组越界,遍历到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}单趟多组:
int gap = 3;//假设gap为3for (int j = 0;j < gap;j++){for (int i = j;i < n - gap;i += gap) //为防止数组越界,遍历到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}}降低循环层次的办法:
上面是一组一组来排,下面代码是每组并发的排序;如果有gap组,那么就从每组的首元素开始遍历至末尾
int gap = 3;//假设gap为3for (int i = 0;i < n - gap;i ++) //为防止数组越界,遍历到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}
整体:
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int j = 0;j < gap;j++){for (int i = j;i < n - gap;i += gap) //为防止数组越界,遍历到n-gap-1{int end = i;int temp = a[end + gap];while (end >= 0){if (temp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = temp;}}}
}
性能分析:
效率如何被提升的?
最开始,每个数跳得都很快,这时正好数组最无序;最后一次排序(gap == 1),每个数都跳得很慢,但基本上都不怎么需要动了,都可以break掉
正是因为希尔排序的这种特性,数据量越大、重复的数据越多(重复数据多,break多挪动少)希尔排序就越是有优势
时间复杂度 O(N^1.3)
gap组数据,假设忽略掉 +1 (方便运算),gap = n/3 同时 每组有3个元素(第一组有4个元素,也看作是3个)
最坏情况下第一趟预排序的消耗:逆序,(1+2)* n / 3 = n (每组的当中元素向前移动1位,后一个元素向前移动2位,总共有n/3组)
最坏情况下第二趟预排序(gap/3/3 = gap/9)的消耗:逆序,(1+2+3+……+8)* n / 9 = 4n
然而,第一趟预排序结束以后,就大概率无法形成最坏情况逆序了;所以第二次排序的消耗肯定小于4n,具体是多少此处省略(复变函数相关内容)
总共进行了log3(N)次这样的预排序( +1 依旧省略)

5.选择排序
选择排序:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的 数据元素排完 。
优化:定义一个begin,再定义一个end;每次找到最小的放在begin,找到最大的放在end;放完之后begin++,end--
int begin = 0, end = n - 1;while (begin < end){//单趟int mini = begin, maxi = begin;for (int i = begin + 1;i <= end;i++){if (a[i] > a[maxi]) maxi = i;if (a[i] < a[mini])mini = i;}Swap(&a[begin], &a[mini]);Swap(&a[end], &a[maxi]);begin++;end--;}循环起止条件:最大值最小值初始化时都是begin下标元素,因此无需再次进行比较;end位置元素没被用来初始化,因此需要遍历到end进行判断比较大小
代码问题:如果maxi在begin位置,mini在begin+1位置;那么在第一个交换语句后,maxi位置的值会被覆盖为最小值;所以需要在 maxi == begin 时,把maxi用mini覆盖掉(此时mini位置存着最大值,maxi位置存着最小值)

void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){//单趟int mini = begin, maxi = begin;for (int i = begin + 1;i <= end;i++){if (a[i] > a[maxi]) maxi = i;if (a[i] < a[mini])mini = i;}Swap(&a[begin], &a[mini]);if (maxi == begin) maxi = mini;Swap(&a[end], &a[maxi]);begin++;end--;}
}6.堆排序
详见文章:堆复习(C语言版)
void Swap(int* a, int* b)
{int c = *a;*a = *b;//把a地址处的元素变为b位置处的元素*b = c;
}void AdjustDown(int* a, int n, int parent)
{//先假设左孩子小int child = parent * 2 + 1;//如果child >= size(n),说明已经到了叶子节点,停止循环while (child < n){//找出小的那个孩子(先得判断有没有右孩子,这也就是假设左孩子小,不假设右孩子小的原因)if (child + 1 < n && a[child + 1] > a[child])child++;//右孩子比较小,改为右孩子//交换or不交换位置,父节点小于小的子节点时,说明找到了该在的位置if (a[parent] >= a[child])break;else{Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}}
}void HPSort(int* a, int n)
{//for (int i = 1; i < n; i++)//Adjustup(a, i); //向上调整建立小堆操作,时间复杂度为nlognfor (int i = (n - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, n, i);//从最后一个父节点开始,依次向下调整,直到调整到根节点为止,时间复杂度为nint end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
