冒泡排序详解

一、概述

冒泡排序（Bubble Sort）是最简单和最通用的排序方法，其基本思想是：在待排序的一组数中，将相邻的两个数进行比较，若前面的数比后面的数大就交换两数，否则不交换；如此下去，直至最终完成排序 。由此可得，在排序过程中，大的数据往下沉，小的数据往上浮，就像气泡一样，于是将这种排序算法形象地称为冒泡排序。

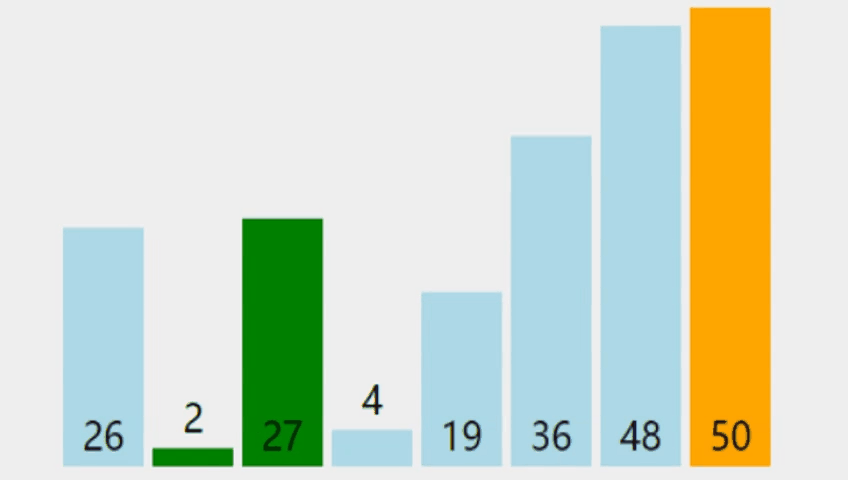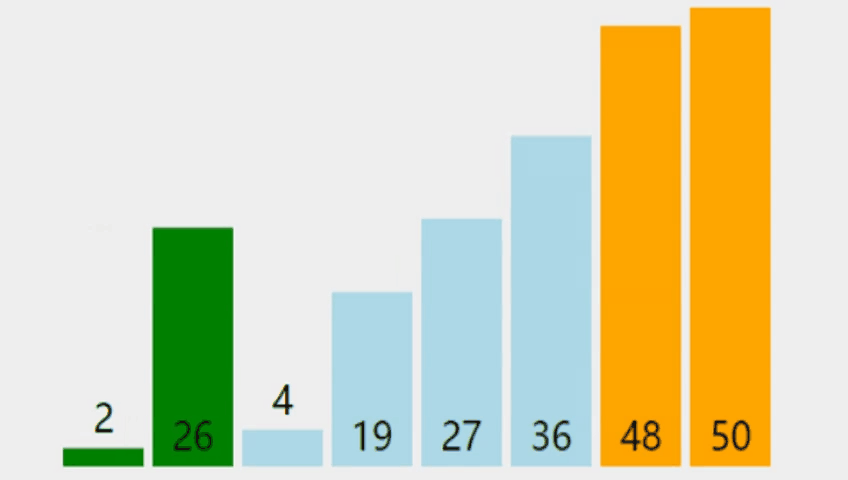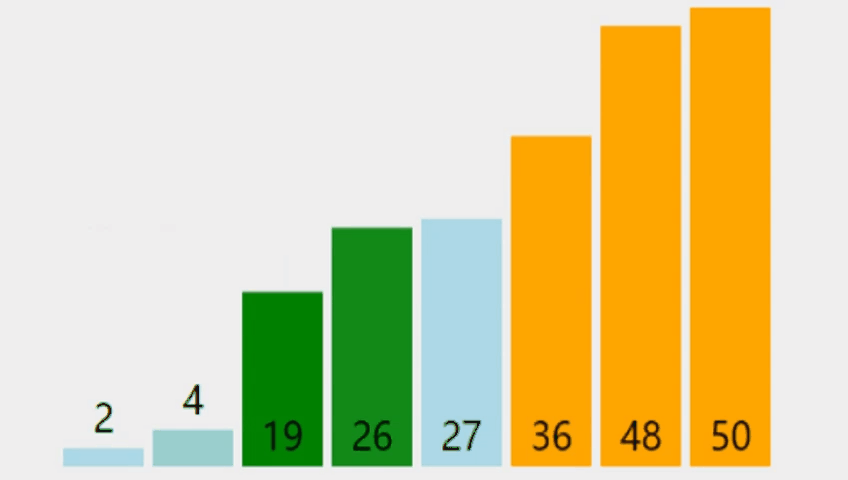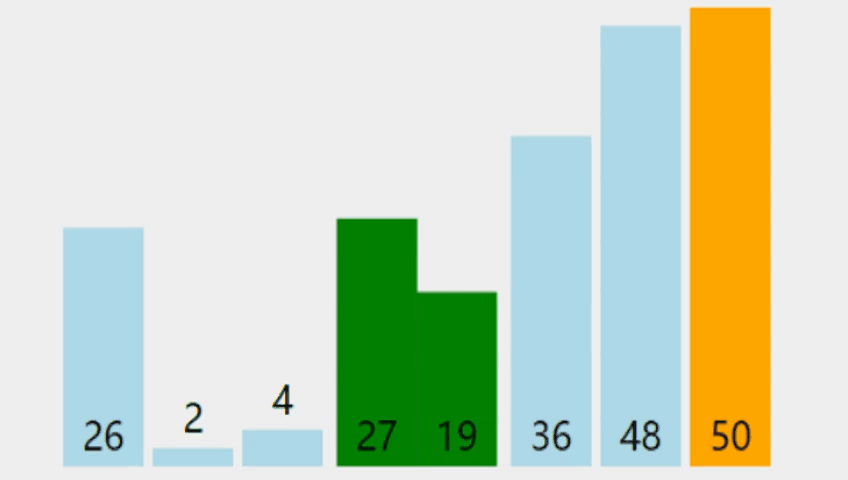
直接讲算法未免过于生硬，让我们从一道题目开始学习吧！👇🏼

---

二、引入

luogu P1116 车厢重组

分析题干，题目给定n节车厢，我们需要对其按编号从小到大排序；我们只有一种方法——将相邻两节车厢的位置交换，问最少需要多少步完成排序。

✔️这种只能对相邻两个位置进行交换的排序就是我们今天要学习的排序——冒泡排序

三、基本思想

• 从刚才的题目中我们了解到，冒泡排序是一种只对相邻两个位置进行交换的排序。

❔那么我们如何通过这种操作实现序列的有序化呢？

• 假设有一组无序序列 —— a = {4, 3, 2, 1}

🥦 第一趟排序

第一步：对a[0]和a[1]进行比较，出现逆序对，交换a[0]和a[1]

• 此时序列 a = {3, 4, 2, 1}。成功把大的数换到了下标大的位置。

❔那么接下来我们要如何操作呢?

✔️分析可知，此时我们可以进行三种操作
（1）对a[0]和a[1]比较
☑️如果选择操作（1），那么序列将不会有任何改变，因为上次操作已经比较过这两个数了，因此操作（1）不可取。

（2）对a[1]和a[2]比较
☑️如果选择操作（2），此时a[1]为 a序列中前2位的最大值。我们将它和比他下标大的a[2]进行比较，在比较后，可以保证 a[2]是a序列中前3位的最大值。
（3）对a[2]和a[3]比较
☑️如果选择操作（3），那么a[2]和a[3]两个数将和a[0]和a[1]一样成为局部有序的子序列。

第二步：我们对分析的操作（2）和操作（3）进行分类讨论

• 我们先来分析操作（3），经过该操作后，序列 a = {3, 4 ,1 ,2}。

✔️此时我们只剩一种操作（其他两种操作已经完成了，重复使用将无意义） ，对a[1]和a[2]进行比较。比较完成后 序列变为 a = {3, 1, 4 ,2}。

☑️可见经过三次操作后，这种方案没有让序列确定下某个位置的数，虽然通过特定的操作仍能正确的给出答案，但是代码的逻辑比较复杂，可读性差。

• 我们来分析操作（2），经过该操作后，序列 a = {3, 2, 4, 1}
  ☑️在比较后，可以保证 a[2]是a序列中前3位的最大值。

第三步：对a[2]和a[3]进行比较，出现逆序对，交换a[2]和a[3]

ps:至于为什么不讨论a[0]和a[1]，其情况和操作（3）类似，此处就不作过多赘述。

• 经过最后一次操作后，a = {3, 2, 1, 4} 此时序列中最后一位数已经被确定下来了（序列的最大值被确定）

✔️至此，第一趟排序完成，当前序列的最大值固定到序列最后的位置。

🔴后面的排序操作和第一趟排序类似，每趟排序能确定当前序列的最大值并固定它的位置。

🍅 第二趟排序

4的位置已经被确定，因此只需要对前三个数进行排序即可：

（1）a = {3, 2, 1, 4} 👉🏽 a={2, 3, 1, 4} ------- a[0]和a[1]比较，3比1大，交换
（2）a={2, 3, 1, 4} 👉🏽 a={2, 1, 3, 4} ------- a[1]和a[2]比较，3比2大，交换

🍆 第三趟排序

3的位置已经被确定，因此只需要对前二个数进行排序即可：

a = {2, 1, 3, 4} 👉🏽 a={1, 2, 3, 4}** ------- a[0]和a[1]比较，2比1大，交换

• 第三趟排序过后，4个数的序列完成了有序化。

🟤因此，冒泡排序是从前向后（或从后向前），相邻两位依次比较，如果出现逆序对则交换位置，使较大的值移向序列的尾部（或较小的值移向序列的首部）的排序。

❔如果在第n-1趟前排序中出现序列已经有序的情况呢？

☑️序列已经有序，无需继续排序和比较，因此我们可以使用一个布尔值（bool）标记，如果序列已经有序则跳出循环。

🍒 规律小结

（1）n个数的序列需要n-1趟排序，每趟排序能确定当前序列的最值并固定它的位置。
（2）每趟排序需要的比较次数逐渐减少——局部有序。
（3）如果在某趟排序中，序列没有一次交换（序列已经有序），则跳出循环。

四、代码实现

🟠这里提供两种冒泡模板
（1）大值移向尾部的冒泡

//模板一
bool f=false;
for(int i=0;i<n;i++)for (int j = 0; j < n-i-1; j++) {if (a[j] > a[j + 1])//比较相邻元素{int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;f=true;}if(!f) break;//序列已经有序else f=false;}

（2）小值移向首部的冒泡

//模板二
bool f=false;
for(int i=0;i<n;i++)for (int j = n-1; j > i; j--) {if (a[j] < a[j - 1])//比较相邻元素{int tmp = a[j];a[j] = a[j - 1];a[j - 1] = tmp;}if(!f) break;//序列已经有序else f=false;}

• 这时我们回过头去看这道题目，就知道该如何下手了

#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
#define rep(i,a,n) for (int i=a;i<=n;i++)//i为循环变量，a为初始值，n为界限值，递增
#define per(i,a,n) for (int i=a;i>=n;i--)//i为循环变量， a为初始值，n为界限值，递减。
#define eb emplace_back
#define pb push_back
#define all(a) a.begin(), a.end()
#define ios ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
#define fi first
#define se second
typedef long long ll;
const int inf = 0x3f3f3f3f;//无穷大 
const int N = 2e4 + 10;;
const int M = 1e6 + 300;
typedef pair<int, int>PII;
int t;
ll a[N];
int main()
{ios;ll n; cin >> n;for (int i = 0; i < n; i++)cin >> a[i];bool f = false;//用于标记当前排序是否进行过交换操纵ll ans = 0;//记录交换次数for (int i = 0; i < n; i++) {for (int j = n - 1; j > 0; j--)if (a[j] < a[j - 1]){int tmp = a[j];a[j] = a[j - 1];a[j - 1] = tmp;f = true;ans++;}if (!f) break;else f = false;}cout << ans;return 0;
}

可以看到成功通过了评测

五、总结和提炼

最后我们总结一下本文学到的内容

1. 【冒泡排序】每次比较相邻两个元素，如果它们不符合要求（升序或降序），就交换它们的位置。

2. 每一趟排序后，未排序序列中最大的元素（或者最小的元素）会被交换到序列的尾部。

3. n个数的序列需要n-1趟排序，每趟排序能确定当前序列的最值并固定它的位置。

4. 在每一轮遍历中，最大的未排序元素会被移动到其最终位置。因此，随着遍历的进行，已排序的子序列会逐渐增长，而未排序的子序列会逐渐缩短。

5. 时间复杂度分析：如果序列已经有序则只需要一趟排序。时间复杂度为 O(N)。序列为逆序，需要进行n-1轮遍历。时间复杂度为 O(N²)。

6. 稳定性分析：【冒泡排序】是稳定的排序算法，即相同元素的相对顺序在排序过程中不会改变。

好，这就是本文的所有内容了，有不足的地方可以在评论区提出，如果觉得还不错可以点个赞(ô‿ô)