Graph Representation Learning【图最短路径优化/Node2vec/Deepwalk】

Q1：

DDI网络构建无向图并找出指定节点i和j的所有最短距离

DDI网络可表示为：
G s m a l l = ( V s m a l l , E s m a l l ) V s m a l l = { 1 , 2 , 3 , 4 } E s m a l l = { ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 3 , 4 ) } G_{small}=(V_{small},E_{small})\\ V_{small}=\{1,2,3,4\} \\E_{small}=\{(1,2),(1,3),(1,4),(3,4)\} Gsmall​=(Vsmall​,Esmall​)Vsmall​={1,2,3,4}Esmall​={(1,2),(1,3),(1,4),(3,4)}

网络性质：

无向无权的大规模稀疏图，我们一般用邻接表存储：

1.数据读取与邻接表构建：

​ 遍历所有边，为每个节点维护其邻接节点列表。对于边 ( (u, v) )，将 ( v ) 加入 ( u ) 的邻接列表，并将 ( u ) 加入 ( v ) 的邻接列表。
Adj [ u ] ← Adj [ u ] ∪ { v } , Adj [ v ] ← Adj [ v ] ∪ { u } \text{Adj}[u] \leftarrow \text{Adj}[u] \cup \{v\}, \quad \text{Adj}[v] \leftarrow \text{Adj}[v] \cup \{u\} Adj[u]←Adj[u]∪{v},Adj[v]←Adj[v]∪{u}

2.基本特征和连通性：

通过dfs得到图的连通性结果如下

• 每个节点平均连接到大约47个其他节点

• 这意味着整个图是一个单一的连通组件，没有孤立的子图，整个网络是完全连通的，任何两个节点之间都存在路径相连

以下为度数分布图：

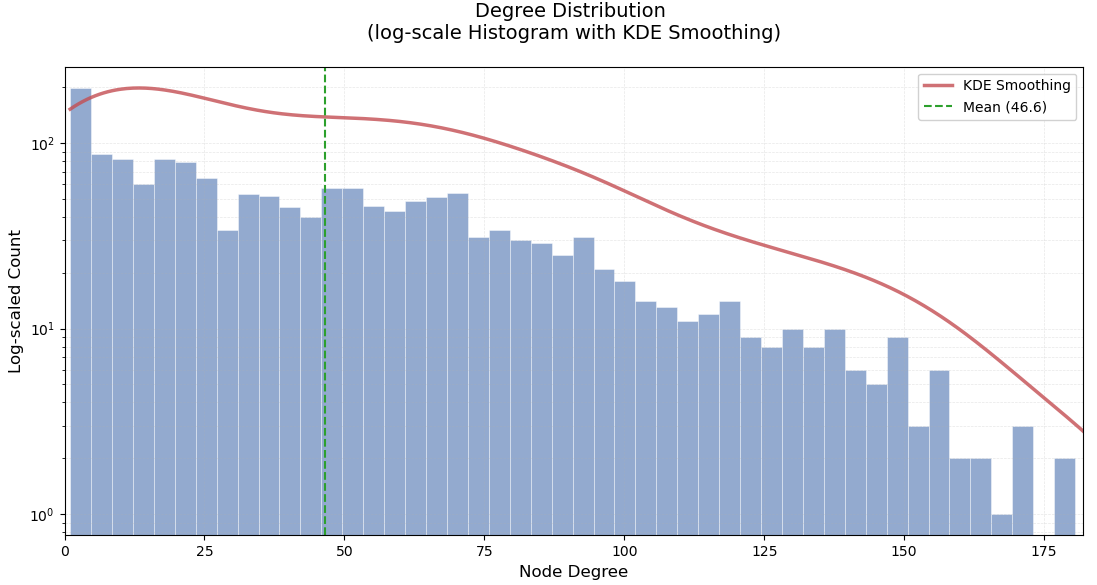
算法思路：

• 寻找两点之间的所有最短路径，使用**BFS+回溯**, 因为由上面的分析可知，图的平均度数很高，较为密集，最短路径长度较短，所以递归深度不会太高。
• 但是在路径回溯阶段，虽然直观易实现，但在最短路径数量较多的情况下，递归深度和调用栈开销可能迅速增长，性能下降甚至栈溢出。所以先使用显式栈进行迭代回溯。
• 在回溯过程中，某些节点的路径可能会被多次访问。记忆化缓存可以保存已经计算过的路径，避免再次计算。

1. 广度优先搜索（BFS）标记前驱:

1. 初始化距离 (d[s] = 0)，其余节点 ( d[v] = inf )。
2. 使用队列逐层扩展，更新节点的最短距离和前驱节点：
   ∀ v ∈ Adj [ u ] , 若  d [ v ] > d [ u ] + 1 ⟹ d [ v ] ← d [ u ] + 1 , prev [ v ] ← { u } 若  d [ v ] = d [ u ] + 1 ⟹ prev [ v ] ← prev [ v ] ∪ { u } \forall v \in \text{Adj}[u], \quad \text{若 } d[v] > d[u] + 1 \implies d[v] \leftarrow d[u] + 1, \ \text{prev}[v] \leftarrow \{u\} \\ \text{若 } d[v] = d[u] + 1 \implies \text{prev}[v] \leftarrow \text{prev}[v] \cup \{u\} ∀v∈Adj[u],若 d[v]>d[u]+1⟹d[v]←d[u]+1, prev[v]←{u}若 d[v]=d[u]+1⟹prev[v]←prev[v]∪{u}
3. 当队列为空时结束。

2. 回溯生成所有最短路径:

从终点 ( t ) 启动，使用显式栈模拟递归过程，逐步构建所有从起点 ( s ) 到终点 ( t ) 的最短路径。与传统的回溯方法不同，这里我们利用记忆化搜索来缓存计算过的路径，以减少不必要的重复计算。

• 使用栈中元素表示当前遍历状态：(当前节点, 当前路径)。
• 如果当前节点是起点 s，则路径已经完整，逆序将路径加入结果集中。
• 如果当前节点不是起点，首先检查该节点是否已经有缓存路径（通过 memo 字典）。如果有，则直接从缓存中取出路径；否则，遍历当前节点的前驱节点，将所有可能的路径推入栈中。

实验结果：

对于（8,309）、（67,850）、（990,1256）药物的最短路径：

使用time模块：对于最短路径较多的用时较少。

复杂度分析：

• BFS会遍历所有边和节点来计算最短路径，并且回溯最短路径时涉及到路径构建
• 实际最坏时间复杂度比没有缓存时更低，但是由于使用了记忆化搜索，减少了重复计算

$$\begin{gathered} O(E+(V+E)+K\cdot L) \\ V为节点数，E为边数，K是路径数量,L是路径最大长度 \end{gathered}$$

Q2：

计算所有正负药物对的最短距离并可视化对比两类样本的结果

列表	数据含义	药物对的数量
DDIpos	DDI网络中存在相互作用的药物对（正样本）	1601
DDIneg	DDI网络中没有相互作用的药物对（负样本）	1601

算法思路：

• 不同于Q1寻找所有的最短路径, 要计算大量节点间的最短距离，所以我们之间使用BFS即可，考虑到效率，特别是在查询较长路径时，尝试双向广度优先搜索。
• 从起点和终点同时开始搜索，直到两者相遇。这样可以显著减少搜索的空间，尤其是对于大的图，因为搜索空间的半径会从两个方向扩展，通常比从一个方向全图扩展要小。

1. 初始化

   定义两个队列 Q_s、Q_t，分别从起点 s 和终点 t 启动：
   $$\text{dist}(s,s)=0,\text{dist}(t,t)=0$$

2. 交替扩展搜索队列：

   • 从 Q_s 中取出节点 u 及其当前距离 d_s，对每个邻居 w：

     $$w\notin {\text{visited}}_s\Rightarrow \text{加入 }{Q}_s,\text{dist}(s,w)=d_s+1$$

   • 从 Q_t 中取出节点 v 及其当前距离 d_t，对每个邻居 w'：

     $$w^{\prime }\notin {\text{visited}}_t\Rightarrow \text{加入 }{Q}_t,\text{dist}(t,w^{\prime })=d_t+1$$

3. 路径相遇判定：
   当存在某个节点
   $$x\in {\text{visited}}_s\cap {\text{visited}}_t$$
   最短路径长度为：
   $$\text{dist}(s,t)=\text{dist}(s,x)+\text{dist}(t,x)$$

4. 不可达判断：
   若两个队列均为空仍未相遇，说明 s 到 t不可达。

实验结果：

正负样本对的距离柱状图如下：

正样本对最短距离几乎都分布在2_{4，负样本对分布在5}6。

复杂度分析：

最短路径长度为 d,即
$$dist(s,t)=d$$
分别从 ( s )、( t ) 同时扩展，搜索深度减半
$$\begin{gathered} 假设图的平均度为\bar{d}，则BFS深度为k时，节点数量近似为O({\bar{d}}^k) \\ 搜索节点数近似为：O({\bar{d}}^{d/2}) \end{gathered}$$

• 最坏情况：要遍历整个图，时间复杂度仍为
  $$O(V+E)V为节点数，E为边数$$

• 平均情况：因搜索深度减半，效率提高：

$$O({\bar{d}}^{d/2})$$

Q3：

对药物节点进行embedding并在嵌入空间计算可视化表征向量的欧式距离/余弦距离，并进行分析比较

图表示学习：

• Deepwalk：一张图上随机生成节点序列，用这些节点序列以Word2vec方法生成embedding。对比Word2vec，把每一个“词”看做节点，得到每个节点的embedding后求两两embedding的余弦相似度，得到top N的近邻排序推荐给目标节点。

• Node2vec：添加控制游走方向的参数，BFS更体现结构性，DFS更体现同质性(远端节点)

  

  • 参数p：控制“回头"概率

  • 参数q：控制偏向BFS or DFS

    

实验结果：

• 节点嵌入:dimensions=128,walk_length=30，num_walk=100

• node2vec: 超参设置不同，对比实验结果如下:

boxplot绘制直观展示：

结果分析：

• Deepwalk：采用 均匀 的随机步长探索邻域。这样，DeepWalk 强调的是 节点之间的共现频率，由于没有对邻域进行加权或偏向某一类邻域结构，DeepWalk 对 直接连接节点对 的敏感度相对较低，无法很好地区分 局部 邻域的细节。
• Node2vec:
  • 当 p 值较小，q 值较大时，Node2Vec 强调 局部邻域结构。此时，模型倾向于对 直接连接的节点对 给予较高的权重，使得正样本（直接连接的节点对）的欧氏距离显著小于负样本。这使得 局部结构 更容易被区分。虽然这种设置能够有效提高欧氏距离的区分度，但 余弦距离 的区分度相对较弱，因为它对空间的聚集性不如欧氏距离敏感。
  • 当 p 值较大，q 值较小时，Node2Vec 强调 全局结构，类似于 深度优先搜索（DFS）。在这种设置下，Node2Vec 更倾向于 捕捉较远的、非直接连接节点的关系，从而使得正负样本在 余弦距离 上的分布更加分散，区分度更佳。但与此同时，由于较大 p 值导致的 探索全局结构，负样本和正样本的 欧氏距离 变得相对较小，且整体的聚集度较高。

ps：为什么不同距离度量的样本区分度大有不同？

如果主要关注近邻节点，直接相连的节点关注度较高，欧氏距离更容易区分，而余弦距离 的区分度较弱，因为余弦距离对相似性度量的需求更加依赖于 整体方向，而不单单是相对距离。但是如果更倾向捕捉到节点在 全局图结构中的角色，正负样本的 欧氏距离 会趋于较小，因为这时节点间的连接不再仅限于直接邻域。

别的尝试：

• 鉴于图神经网络具备端到端训练的能力，后尝试采用生成式模型来学习节点的表示（embedding），GAE 与 VGAE 本质上建模的是图数据的生成过程，因此在理论上具备较强的表达能力。
• 但是，查阅到文献中普遍指出这类模型依赖于节点的属性信息作为输入特征。而在本实验中，图中仅包含节点及其连接关系，缺乏节点特征，因此只能使用全1或one-hot等虚拟特征作为替代。在这种特征缺失的情况下，模型难以从输入中学习到有效的结构区分信息，最终导致 GAE/VGAE 的实验表现明显低于Node2Vec 方法。

参考：

[1] CS224W | Home (stanford.edu)

[2] 1.1 - Why Graphs_哔哩哔哩_bilibili

[3] Graph Embedding - (maelfabien.github.io)

[4] rfp0191-wangAemb.pdf (kdd.org)