当前位置：首页 > news >正文

C++：二叉搜索树

news 来源：原创 2025/5/15 5:49:47

C++：二叉搜索树

二叉搜索树定义与结构：

定义:

二叉搜索树（Binary Search Tree），也称为二叉排序树或二叉查找树，是一种特殊的二叉树数据结构。

结构:

二叉搜索树是一颗二叉树，每个父节点最多只能拥有两个子节点。对于二叉树的每个节点，它的左子树与它的右子树的值只能小于等于根节点的值。

二叉树的性质：

查找效率高：我们对二叉树的其中一个值进行查找时，当根节点值不等于需要查找的值，那么只会进入该树的左子树或右子树进行查找。最多只会查找该树的高度次。时间复杂度为logn。也就是说当该树有100万个值的时候，最多也只会查找20次。效率是非常客观的。
中序遍历:当我们对二叉搜索树进行中序打印时，输出的值刚好就是有序的。

二叉搜索树的缺点:

二叉搜索树虽好，但也有一个致命的缺陷

如上图，a树和b树同样都属于搜索二叉树，但如果每次插入的值都比根小或者都比根大的时候，就会出现上图的形状。此时再去查找搜索时效率就会直线下降，所以为了防止这种情况，后续就出现了AVL树以及红黑树。

搜索二叉树的实现:

单个节点结构及整棵树的结构：

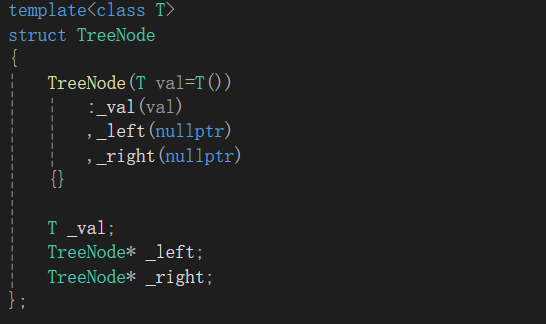
搜索二叉树的插入：

二叉树的插入很简单，将需要插入的值依次跟节点进行比较，大就向左走，小就向又走，最后会走到空。因此我们需要定义一个父节点，当cur走到空时循环退出，cur会new一个新节点，接着判断新节点应该链入父节点的左边还是右边。

二叉树的删除：

二叉树的删除是重点，我们需要分好几种情况去讨论

删除节点没有左子树

比如上图删除6节点，因为6节点的左子树为空，所以我们只需要将6节点的父亲及4节点的right链路6节点的右边，不需要管6是否有又节点。

删除节点没有右子树

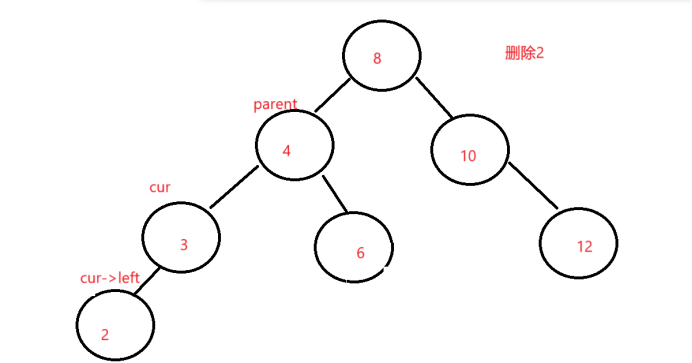
同理，只需要让父节点指向cur的左子树，再释放cur节点即可。
删除节点拥有左右子树

如上图，当我们需要删除4节点的时，因为4拥有左右子树，不能简单直接删除，会破坏二叉搜索树的特性，因此我们需要使用替代法。

一颗树的右子树的最左节点与一颗树的左子树的最右节点，是仅大于该子树的根或仅小于该子树根的节点。如果我们将其中一颗赋值给该子树的根节点时，此时二叉树的结构与特性并不会发生变化，接着在直接再释放原最大节点或最小节点，就完成了删除操作

如上图需要删除4，我们去寻找4的右子树的最左节点也就是5。接着将5节点的值赋给4。但是并不能直接删除5节点，因为5节点只是最左节点，可能5节点右边还有节点。所以我们还需要定义一个parent节点，判断minright是在我parent节点的左边还是右边后再去链路5节点的右边。
删除节点为根节点

如果删除的根节点拥有左右子树时，只需要走例3。但如果删除的根节点只有左或右子树时，我们只需要更新_root节点为_root->left或者_root->right节点，接着再释放原根节点即可

源码及测试代码：
SBTree：

#pragma once
#include<iostream>
#include<string>using namespace std;
//K模型
template<class T>
struct TreeNode
{TreeNode(T val=T()):_val(val),_left(nullptr),_right(nullptr){}T _val;TreeNode* _left;TreeNode* _right;
};template<class T>
class SBTree
{typedef TreeNode<T> Node;
public:bool Insert(const T& val){if(!_root){_root = new Node(val);}else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_val > val){parent = cur;cur = cur->_left;}else if (cur->_val < val){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(val);if (cur->_val > parent->_val){parent->_right = cur;}else{parent->_left = cur;}return true;}}bool Erase(const T&val){Node* cur=_root;Node* parent=nullptr;while (cur){if (cur->_val > val){parent = cur;cur = cur->_left;}else if (cur->_val < val){parent = cur;cur = cur->_right;}else{if(cur->_left==nullptr)//左孩子为空{if(cur==_root){_root = cur->_right;}else{//判断cur是在parent的左还是右if(parent->_left==cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if(cur->_right==nullptr)//右孩子为空{if (cur == _root){_root = cur->_left;}else{//判断cur是在parent的左还是右if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else//左右孩子都不为空{Node* minRight = cur->_right;//右子树的最左节点Node* minRightParent=cur;while(minRight->_left){minRightParent = minRight;minRight = minRight->_left;}cur->_val = minRight->_val;if (minRightParent->_left==minRight){minRightParent->_left = minRight->_right;}else{minRightParent->_right = minRight->_right;}cur = minRight;}delete cur;return true;}}return false;}void Inorder(){return _Inorder(_root);}
private:void _Inorder(Node*cur){if (cur == nullptr)return;_Inorder(cur->_left);std::cout << cur->_val << " ";_Inorder(cur->_right);}Node* _root=nullptr;
};namespace cat
{template<class K, class V>struct BSTNode{BSTNode(const K& key = K(), const V& value = V()): _left(nullptr), _right(nullptr), _key(key), _value(value){}BSTNode<K,V>* _left;BSTNode<K, V>* _right;K _key;V _value;};template<class K, class V>class BSTree{typedef BSTNode<K, V> Node;typedef Node* PNode;public:void Inorder(){return _Inorder(_root);}BSTree() : _root(nullptr) {}PNode Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return cur;}}return nullptr;}bool Insert(const K& key, const V& value){if (!_root){_root = new Node(key,value);}else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key,value);if (cur->_key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}return true;}}private:void _Inorder(Node* cur){if (cur == nullptr)return;_Inorder(cur->_left);std::cout << cur->_key << " " << cur->_value << " ";_Inorder(cur->_right);}PNode _root;};
}

test.cpp

#include"SBTree.h"void test01()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };SBTree<int> st;for(auto &e:a){st.Insert(e);}st.Inorder();std::cout << std::endl;st.Erase(7);st.Inorder();std::cout << std::endl;st.Erase(14);st.Inorder();std::cout << std::endl;st.Erase(3);st.Inorder();std::cout << std::endl;st.Erase(8);st.Inorder();std::cout << std::endl;for (auto& e : a){st.Erase(e);}st.Inorder();
}void TestBSTree4()
{// 统计水果出现的次数string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };cat::BSTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在，说明水果第一次出现，则插入<水果, 1>// 2、在，则查找到的节点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == NULL){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.Inorder();
}
int main()
{test01();//TestBSTree4();return 0;
}

------------------------------------本片文章就到这里，感谢各位观看