当前位置：首页 > news >正文

深度学习之优化器【从梯度下降到自适应学习率算法】（pytorch版）

news 来源：原创 2025/5/18 0:59:52

文章目录

优化器（Optimizer）
二基础优化器
- 1. 梯度下降（Gradient Descent, GD）
- 2. 随机梯度下降（Stochastic Gradient Descent, SGD）
三动量优化算法
- 标准动量优化（Momentum）
- 自适应学习率算法
- - 1. AdaGrad（Adaptive Gradient）
  - 2. RMSprop（Root Mean Square Propagation）
  - 3. Adam（Adaptive Moment Estimation）
- 算法对比与选择指南
PyTorch 优化器比较案例

优化器（Optimizer）

优化器（Optimizer）是深度学习中用于更新模型以最小化（或最大化）损失算法。在机器学习和深度学习中，优化器根据模型的性能指标来调整模型的参数，找到最佳的模型配置。
计算图可以看作一种用来描述计算函数的语言，图中的节点代表函数的操作，边代表函数的输入。
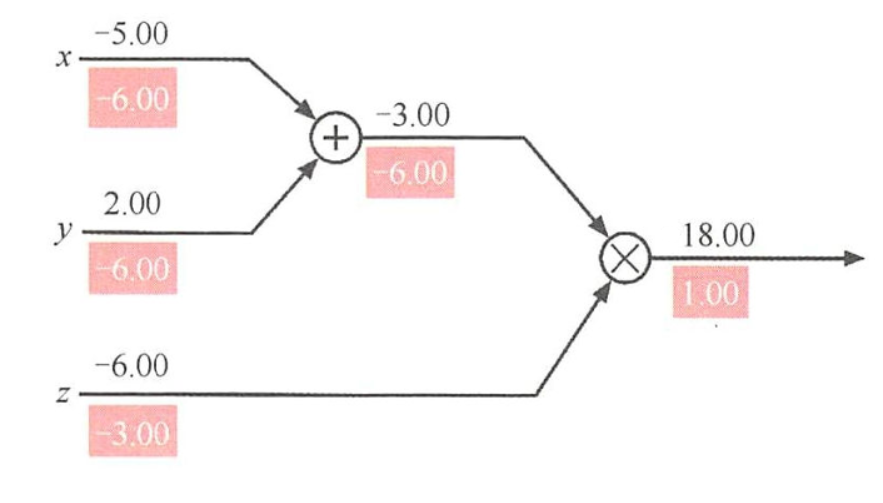
优化器的工作原理基于计算图上的梯度信息，通常遵循以下步骤：

计算损失：模型会对输入数据进行预测，并与真实值比较以计算出损失。
反向传播：使用链式法则（通过自动求导框架，如PyTorch的.backwardO方法）计算损失相对于模型参数的梯度。
更新权重：优化器使用这些梯度来更新模型的权重。

常见的优化器有梯度下降（Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）、标准动量优化算法，以及一系列自适应学习率算法，如AdaGrad、RMSprop和Adam。

二基础优化器

1. 梯度下降（Gradient Descent, GD）

算法原理：梯度下降是最基础的优化算法，通过计算整个训练集上损失函数的梯度来更新参数：
$θ = θ - η \cdot \nabla J (θ)$
η是学习率，∇J(θ)是损失函数对参数θ的梯度。
特点：每次更新需要计算整个数据集的梯度，计算成本高；对于凸函数能保证收敛到全局最优，非凸函数可能收敛到局部最优；学习率固定，难以适应不同参数的需求
适用场景：小型数据集；理论研究或教学示例

2. 随机梯度下降（Stochastic Gradient Descent, SGD）

算法原理：SGD每次随机选取一个样本计算梯度并更新参数：
$θ = θ - η·∇J(θ; x_i; y_i)$
特点：计算效率高，适合大规模数据集；由于噪声的存在，可能帮助跳出局部最优；学习率需要精心设计；收敛过程波动较大
改进版本：Mini-batch SGD：折中方案，使用小批量样本计算梯度

三动量优化算法

标准动量优化（Momentum）

算法原理：标准动量优化（Momentum）算法则将动量运用到神经网络的优化中，用累计的动量来替代真正的梯度，计算负梯度的“加权移动平均”来作为参数的更新方向
$\Delta \theta_t = \rho \Delta \theta_{t-1} - \alpha g_t$
$\rho$ 是动量因子，通常设为0.9， $\alpha$ 为学习率。
特点：加速SGD在相关方向的收敛；抑制震荡，帮助越过局部最优；仍然需要手动设置学习率

自适应学习率算法

自适应学习率算法通过自动调整各参数的学习率，解决了传统方法需要手动调参的问题。

1. AdaGrad（Adaptive Gradient）

AdaGrad算法借鉴正则化思想，每次迭代时自适应地调整每个参数的学习率，在进行第t次迭代时，先计算每个参数梯度平方的累计值。
算法原理：为每个参数维护一个梯度平方的累积变量，自动调整学习率：
$\sum _ { i = 1 } ^ { t } g _ { i } \odot g _ { i } \\$
$\odot$ 为按元素乘机， $g_t$ 是第 $t$ 次迭代时的梯度，然后计算参数的更新差值，表达式为：
$\Delta \theta _ { t } = - \frac { \alpha } { \sqrt { G _ { t } + \varepsilon } } \odot g _ { t }$
特点：稀疏特征对应的参数获得更大的更新；适合处理稀疏数据；学习率单调递减，后期可能过小导致训练提前终止
优点：自动调整学习率；适合稀疏数据
缺点：累积平方梯度导致学习率过早衰减；对初始学习率敏感

2. RMSprop（Root Mean Square Propagation）

RMSProp算法对AdaGrad算法进行了改进，在AdaGrad算法中由于学习率逐渐减小，在经过一定次数的迭代依然没有找到最优点时，便很难再继续找到最优点，RMSProp算法则可在有些情况下避免这种问题。
算法原理：改进AdaGrad的激进衰减问题，引入衰减系数。RMSProp算法首先计算每次迭代梯度 $g_t$ 平方的指数衰减移动平均
$\beta G _ { t - 1 } + \left( 1 - \beta \right) g _ { t } \odot g _ { t }$
$\beta$ 为衰减率，然后用和AdaGrad算法同样的方法计算参数更新差值，RMSProp算法的每个学习参数的衰减趋势既可以变小又可以变大。

特点：使用指数移动平均代替累积和；解决了AdaGrad学习率单调递减问题；适合非平稳目标和RNN训练
优点：自适应学习率；解决了AdaGrad的激进衰减
缺点：仍然依赖全局学习率；超参数γ需要调整

3. Adam（Adaptive Moment Estimation）

Adam算法即自适应动量估计算法，是Momentum算法和RMSProp算法的结合，不但使用动量作为参数更新方向，而且可以自适应调整学习率。
算法原理：结合动量思想和自适应学习率
$\begin{array} { r l } & { M _ { t } = \beta M _ { t - 1 } + \left( 1 - \beta _ { 1 } \right) g _ { t } } \\ & { G _ { t } = \beta G _ { t - 1 } + \left( 1 - \beta _ { 2 } \right) g _ { t } \odot g _ { t } } \end{array}$
$\beta_1$ 和 $\beta_2$ 分别为两个移动平均的衰减率，Adam算法的参数更新差值
$\Delta \theta _ { t } = - \frac { \alpha } { \sqrt { G _ { t } + \varepsilon } } \odot M _ { t }$

特点：结合了动量（Momentum）和RMSprop的优点；对内存需求较小；适合大数据集和高维空间；默认参数通常表现良好。
优点：自适应学习率，收敛速度快，对超参数鲁棒性强
缺点：可能不收敛到最优解，个别情况下可能不如SGD+momentum

算法对比与选择指南

优化器	收敛速度	内存需求	稀疏数据	超参数敏感性	适用场景
SGD	慢	低	一般	高	理论研究
Momentum	中等	低	一般	中	稳定收敛
AdaGrad	中等	中	优秀	中	稀疏数据
RMSprop	快	中	良好	中	RNN/非平稳
Adam	很快	中	良好	低	通用场景

Adam通常是首选，尤其在不清楚该用什么时
对于稀疏数据可尝试AdaGrad
训练RNN时RMSprop表现良好
追求极致性能时可尝试SGD+动量+学习率调度
理论研究时常用SGD以便分析

PyTorch 优化器比较案例

import torch
import torch.nn
import torch.utils.data as data
import matplotlib.pyplot as plt# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题，确保在图表中正确显示负号
plt.rcParams['axes.unicode_minus'] = False# 生成数据集
x=torch.unsqueeze(torch.linspace(-1,1,500),dim=1)
y=x.pow(3)# 设置超参数
LR=0.01 # 学习率
batch_size=15 # 批量大小
epoches=5 # 迭代轮数
torch.manual_seed(10) # 设置随机种子# 设置数据加载器
dataset=data.TensorDataset(x,y)
loader=data.DataLoader(dataset, # 数据集batch_size, # 批量大小shuffle=True, # 打乱数据num_workers=2 # 线程数)# 搭建神经网络框架
class Net(torch.nn.Module):# 定义网络结构def __init__(self,  n_input, n_hidden, n_output):super(Net,self).__init__()self.hidden_layer=torch.nn.Linear(n_input,n_hidden) # 隐藏层self.output_layer=torch.nn.Linear(n_hidden,n_output) # 输出层#  定义前向传播def forward(self,input):x=torch.relu(self.hidden_layer(input))return self.output_layer(x)# 训练模型并输出折线图
def train():"""训练多个不同优化器的神经网络模型，并绘制损失曲线:return:"""# 定义神经网络模型net_SGD=Net(1,10,1)net_Momentum=Net(1,10,1)net_AdaGrad=Net(1,10,1)net_RMSprop=Net(1,10,1)net_Adam=Net(1,10,1)# 存储神经网络模型列表nets=[net_SGD, net_Momentum, net_AdaGrad, net_RMSprop, net_Adam]# 定义优化器optimizer_SGD=torch.optim.SGD(net_SGD.parameters(),lr=LR)optimizer_Momentum=torch.optim.SGD(net_Momentum.parameters(),lr=LR,momentum=0.6)optimizer_AdaGrad=torch.optim.Adagrad(net_AdaGrad.parameters(),lr=LR,lr_decay=0)optimizer_RMSprop=torch.optim.RMSprop(net_RMSprop.parameters(),lr=LR,alpha=0.9)optimizer_Adam=torch.optim.Adam(net_Adam.parameters(),lr=LR,betas=(0.9,0.99))# 存储优化器列表optimizers=[optimizer_SGD, optimizer_Momentum, optimizer_AdaGrad, optimizer_RMSprop, optimizer_Adam]# 均方误差函数loss_function=torch.nn.MSELoss()# 存储每个模型损失值列表losses=[[],[],[],[],[]]for epoche in range(epoches):for step,(batch_x,batch_y) in enumerate(loader):# 按模型、优化器和损失值列表的顺序循环for net,optimizer,loss_list in zip(nets,optimizers,losses):# 前向传播output=net(batch_x)# 计算损失loss=loss_function(output,batch_y)# 清空梯度optimizer.zero_grad()#  反向传播计算梯度loss.backward()# 更新参数optimizer.step()# 将损失值添加到列表loss_list.append(loss.data.numpy())# 创建图像plt.figure(figsize=(12,7))# 定义标签labels=['SGD','Momentum','AdaGrad','RMSprop','Adam']for i,loss in enumerate(losses):# 绘制每个模型的损失函数plt.plot(loss,label=labels[i])# 添加图例plt.legend(loc='upper right',fontsize=15)# 设置刻度字体大小plt.tick_params(labelsize=13)plt.xlabel('训练步骤',fontsize=15)plt.ylabel('模型损失',fontsize=15)plt.ylim((0,0.3))plt.title('不同优化器的损失函数曲线',fontsize=15)plt.show()if  __name__=='__main__':train()