牛客周赛96补题 D F
D 数学
已知有两根,用韦达公式
- x 2 − p x + q = 0 → x 1 + x 2 = p , x 1 x 2 = q x^2-px+q=0\rightarrow x_1+x_2=p,x_1x_2=q x2−px+q=0→x1+x2=p,x1x2=q
- x 1 + x 2 + x 1 x 2 + 1 = p + q + 1 = k + 1 → ( x 1 + 1 ) ( x 2 + 1 ) = k + 1 x_1+x_2+x_1x_2+1=p+q+1=k+1\rightarrow (x_1+1)(x_2+1)=k+1 x1+x2+x1x2+1=p+q+1=k+1→(x1+1)(x2+1)=k+1
赛时舍近求远去推了一大堆求根公式…
void solve()
{int k;cin>>k;for(int i=1;i*i<=(k+1);i++){if((k+1)%i==0){int j=(k+1)/i;int a=i-1,b=j-1;if(a>0&&b>0){cout<<a+b<<' '<<a*b<<endl;return;}}}cout<<-1<<endl;
}
F 构造 异或和
- a i , j a_{i,j} ai,j在 R 2 、 L 2 R_2、L_2 R2、L2都被异或进去了,所以 ⨁ i = 1 m R i ⊕ ⨁ j = 1 n C j = 0 \bigoplus\limits_{i=1}^m R_i\oplus\bigoplus\limits_{j=1}^n C_j=0 i=1⨁mRi⊕j=1⨁nCj=0
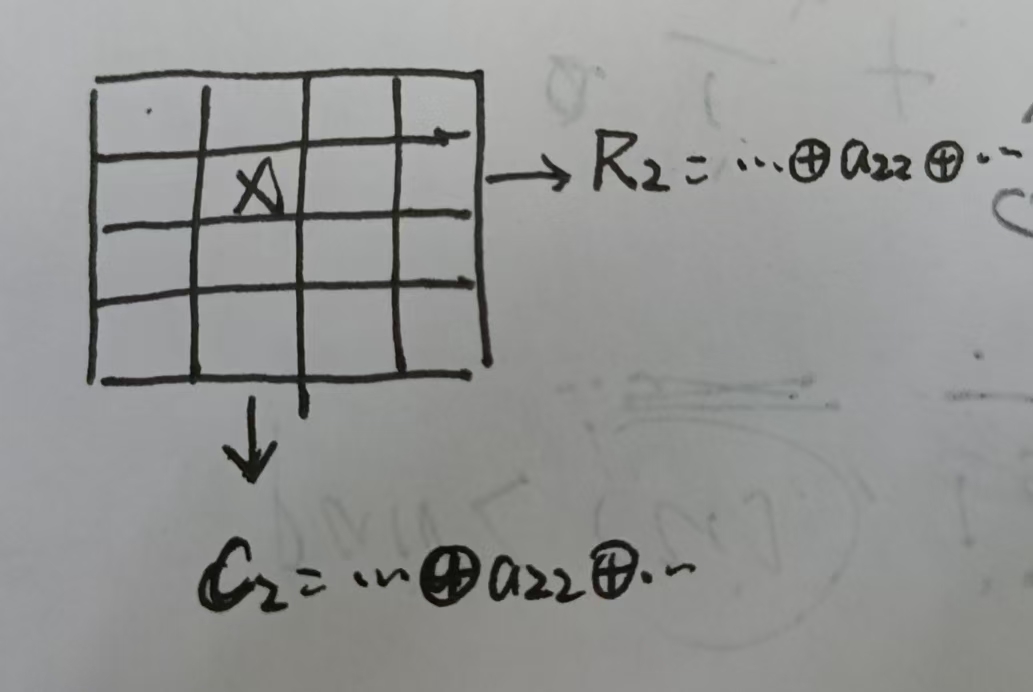
- R、C是n+m的排列,根据前缀异或和性质,下有打表
- p % 4 = 1 , ⨁ x = 1 p x = 1 p\%4=1,\bigoplus\limits_{x=1}^p x=1 p%4=1,x=1⨁px=1
- p % 4 = 2 , ⨁ x = 1 p x = p + 1 p\%4=2,\bigoplus\limits_{x=1}^p x=p+1 p%4=2,x=1⨁px=p+1
- p % 4 = 3 , ⨁ x = 1 p x = 0 p\%4=3,\bigoplus\limits_{x=1}^p x=0 p%4=3,x=1⨁px=0
- p % 4 = 0 , ⨁ x = 1 p x = p p\%4=0,\bigoplus\limits_{x=1}^p x=p p%4=0,x=1⨁px=p
- 可以确定合法条件:(n+m)%4==3

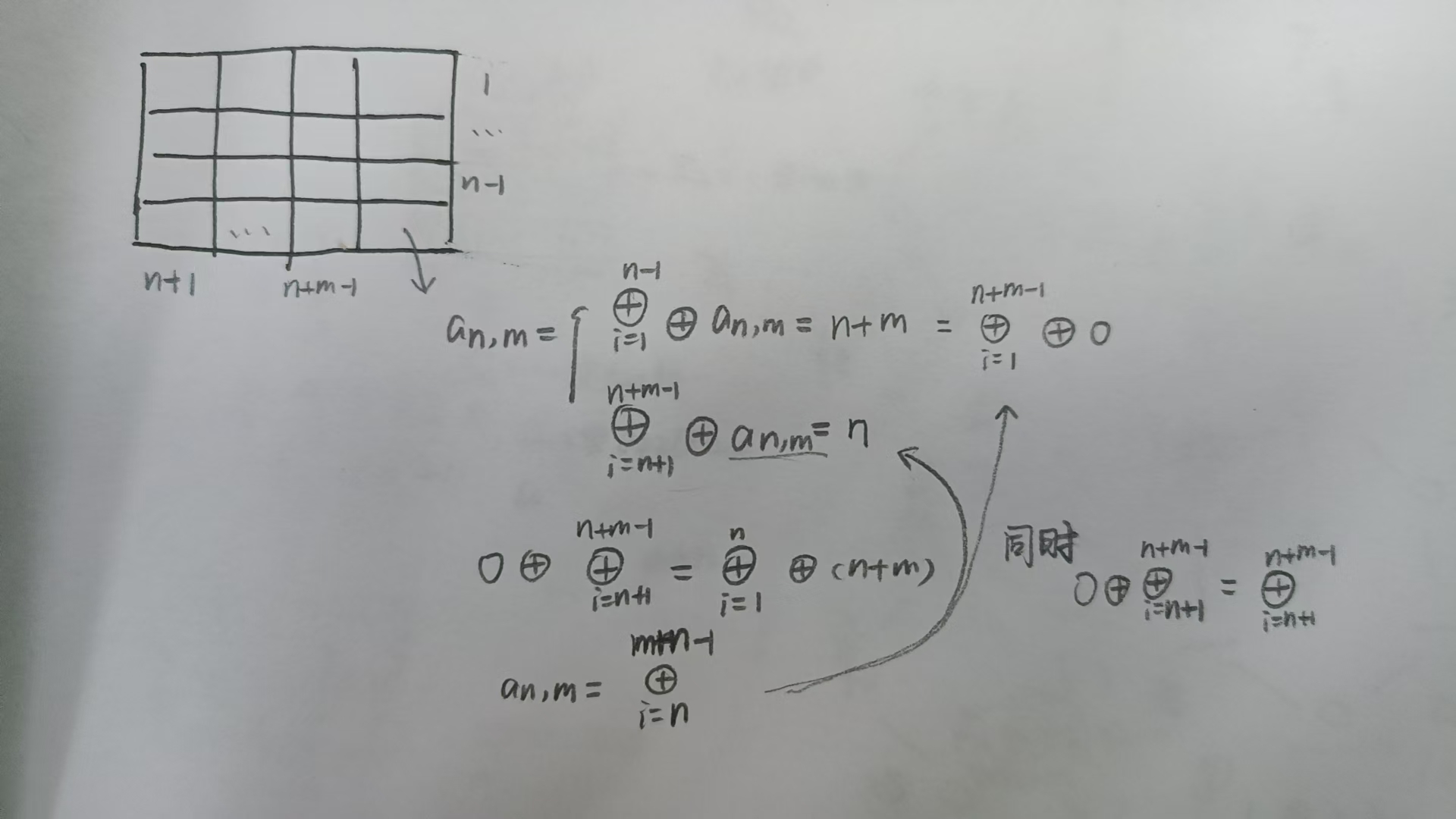
- 构造:
- p ⊕ 0 = p p\oplus0=p p⊕0=p,先构造1~n-1,n+1~n+m-1部分
- 对 a n , m a_{n,m} an,m,利用 p ⊕ p = 0 p\oplus p=0 p⊕p=0和 0 = ⨁ x = 1 p x , p % 4 = 3 0=\bigoplus\limits_{x=1}^p x,p\%4=3 0=x=1⨁px,p%4=3的性质,凑出 a n , m a_{n,m} an,m
void solve()
{//打表代码// int x=0;// forr(i,1,16){// x^=i;// cout<<i<<' '<<x<<endl;// }int n,m;cin>>n>>m;if((n+m)%4!=3)return cout<<-1<<endl,void();vector<vector<int> >a(n+1,vector<int>(m+1,0));forr(i,1,n-1){a[i][m]=i;}forr(j,1,m-1){a[n][j]=n+j;a[n][m]^=(n+j);}// cout<<a[n][m]<<endl;a[n][m]^=n;forr(i,1,n){forr(j,1,m)cout<<a[i][j]<<' ';cout<<endl;}
}
