栈和队列复习(C语言版)
目录
一.栈的概念
二.栈的实现
三.队列的概念
四.队列的实现
五.循环队列的实现
一.栈的概念

可以将栈抽象地理解成羽毛球桶,或者理解成坐直升电梯;最后一个进去的,出来时第一个出来,并且只有一个出入口。这边需要注意的是,栈顶和栈底的位置是人为制定的,只要符合栈顶和栈底的概念就都可以。
二.栈的实现
分别有两种实现方式,数组和链表。
对于单链表来说,插入新数据方便,但是出数据时因为找不到栈顶的前一个结点,所以不方便。
单链表不适用,所以可以通过双向链表的方式。
可是笔者一身反骨,偏要用单链表的方式实现,那么我们可以通过将栈顶和栈地位置互换,然后通过头插的方式插入。因此单链表的方式实际上也可以实现。

有那么多的实现方式,我到底该选哪个呢?
链表和数组实现的性能判断:
相较于单链表,双向链表多了一个指针,空间消耗大;并且同时需要维护2个指针,比较麻烦,因此直接可以排除。
数组实现的缺点在于扩容,但扩容不会每次操作都进行,因此影响不算大。但数组的cpu高速缓存性能远高于单链表,所以在斟酌损益以后,还是数组实现更优。
初始化时,我们需要对top赋初值。那么top应该指向哪呢?

前者是top++再存入,后者是存入以后top++。两种方式都可以,笔者选择的是前一种方式
#include"Stack.h"//入栈:1 2 3 4
//出栈:4 3 2 1 (不绝对,还可以入栈几个数据,然后出栈几个数据)int main()
{st s;Stinit(&s);Stpush(&s, 1);Stpush(&s, 2);Stpush(&s, 3);Stpush(&s, 4);while (!Stempty(&s))//栈的取数据方式会导致:取一遍数据,栈需要将所有已有数据全部删除{printf("%d ", Sttop(&s));Stpop(&s);}Stdestory(&s);return 0;
}//在test.c文件中,其他功能请自行测试#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int datatype;typedef struct Stack
{datatype* a; //动态开辟int top; //栈顶int capacity; //可容纳空间
}st;void Stinit(st* pst);
void Stdestory(st* pst);
void Stpush(st* pst, datatype x);
void Stpop(st* pst);
datatype Sttop(st* pst);
bool Stempty(st* pst);
int Stsize(st* pst);//在Stack.h文件中#include"Stack.h"
void Stinit(st* pst)
{assert(pst);pst->a = NULL;pst->capacity = 0;pst->top = -1;
}
void Stdestory(st* pst)
{assert(pst);free(pst->a);pst->a = NULL;pst->capacity = 0;pst->top = -1;
}
void Stpush(st* pst, datatype x)
{assert(pst);//扩容if (pst->top + 1 == pst->capacity){int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;datatype* tmp = (datatype*)realloc(pst->a, sizeof(datatype) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}pst->a = tmp;pst->capacity = newcapacity;}pst->a[++pst->top] = x;
}
void Stpop(st* pst) //用函数进行封装,易于管理与理解
{assert(pst);pst->top--;
}
datatype Sttop(st* pst)
{assert(pst);assert(pst->top >= 0);return pst->a[pst->top];
}
bool Stempty(st* pst)
{assert(pst);return pst->top == -1;
}
int Stsize(st* pst)
{assert(pst);return ++pst->top;
}
//在Stack.h文件中栈的一些性质:
- 栈的取数据方式会导致:取一遍数据,栈需要将所有已有数据全部删除
- 入栈和出栈操作可以交替进行。因此,假设入栈顺序为 1 2 3 4;出栈可以是各种各样的情况。
三.队列的概念
![]()
由此不难看出,入队顺序假设为 1 2 3 4,那么出队顺序也是 1 2 3 4 。(就像是排队取号用餐,先取号的先去用餐)
队列常常被用来进行广度优先遍历(就比如好友推荐,一圈又一圈的关系圈,找到然后推荐我朋友的朋友。入队我,出队我,入队我的好友;出队我的好友,入队我好友的好友,最后留在队列里只剩下我好友的好友),所以非常重要!!!

四.队列的实现
考虑到队列需要在头部删除,尾部删除(尾插、头删),因此综合考虑使用单链表的方式实现队列。
头插、尾插是主要使用的,因此需要有一个phead、一个ptail记录首位位置。因此,我们就可以把phead,ptail封装起来做成一个函数。
#include"Queue.h"int main()
{Queue q;QueueInit(&q);QueuePush(&q, 1);QueuePush(&q, 2);QueuePush(&q, 3);QueuePush(&q, 4);printf("%d\n",QueueSize(&q));while (!QueueEmpty(&q)){printf("%d", QueueFront(&q));QueuePop(&q);}return 0;
}
//test.c
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int QDataType;typedef struct QueueNode {struct QueueNode* next;QDataType val;
}QNode;//void QueuePush(QNode* phead,QNode* ptail, QDataType x);
//void QueuePop(QNode* phead,QNode* ptail, QDataType x);typedef struct Queue {QNode* ptail;QNode* phead;int size;
}Queue;void QueueDestroy(Queue* q);
void QueueInit(Queue* q);
void QueuePush(Queue* q, QDataType x);
void QueuePop(Queue* q);
int QueueSize(Queue* q);
int QueueFront(Queue* q);
int QueueBack(Queue* q);
bool QueueEmpty(Queue* q);#include"Queue.h"void QueueInit(Queue* q)
{assert(q);q->phead = NULL;q->ptail = NULL;q->size = 0;
}void QueuePush(Queue* q, int x)
{QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc error");return;}newnode->next = NULL;newnode->val = x;if (q->ptail == NULL)q->phead = q->ptail = newnode;else{q->ptail->next = newnode;q->ptail = newnode;}q->size++;}void QueuePop(Queue* q)
{assert(q);assert(q->size != 0);if (q->phead->next == NULL){free(q->phead);q->phead = q->ptail = NULL;}else{QNode* next = q->phead->next;free(q->phead);q->phead = next;}q->size--;
}int QueueSize(Queue* q)
{assert(q);return q->size;
}int QueueFront(Queue* q)
{assert(q);assert(q->phead);return q->phead->val;
}int QueueBack(Queue* q)
{assert(q);assert(q->ptail);return q->ptail->val;
}void QueueDestroy(Queue* q)
{assert(q);QNode* cur = q->phead;while (cur){QNode* next = cur->next;free(cur);cur = next;}q->phead = q->ptail = NULL;q->size = 0;
}bool QueueEmpty(Queue* q)
{assert(q);return q->size == 0;
}五.循环队列的实现

循环队列是有限的空间,如果还有剩余的空间,就可以插入。假定k为整个队列的大小
如果使用数组实现循环队列,head == tail 时为空时为满,会出现假溢出问题
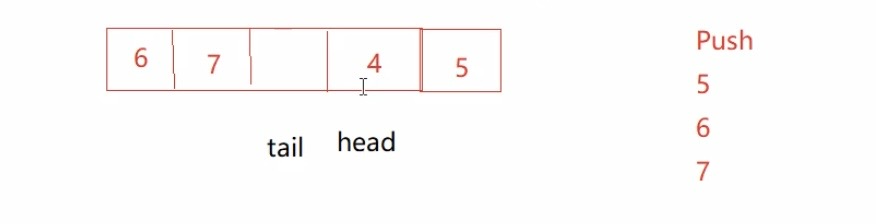
head指向队头 taii指向队尾的后一个元素(如下图1)
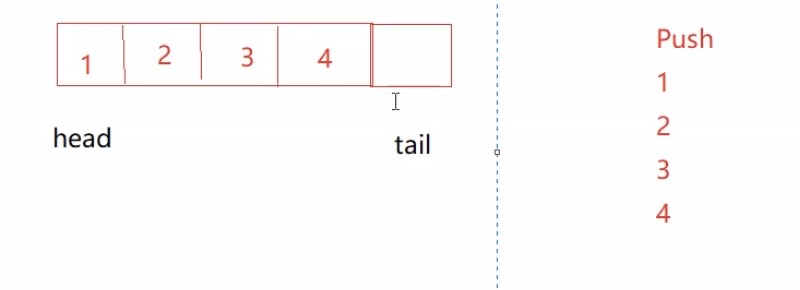
增加一个size/数组多开一个空间( (tail + 1)%(k+1) == head 为满,tail == head 为空) 就可以解决这个问题(解决下图2)
如果使用链表来实现循环链表,找队尾会比较麻烦(没有下标属性);创建链表也比较麻烦,要在Create函数中创建k+1个结点,那么要进行k+1次循环(时间复杂度提升了)
因此不太建议使用链表来实现循环队列
typedef struct {int* a;int head;int tail;int k;
} MyCircularQueue;MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));obj -> a = (int*)malloc(sizeof(int)*(k+1));obj -> head = obj -> tail = 0;obj -> k = k;return obj;
}bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->head == obj->tail;
}bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->tail+1)%(obj->k+1) == obj->head;
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {if(myCircularQueueIsFull(obj)) return false;obj->a[obj->tail++] = value;obj->tail %= obj->k+1;return true;
}bool myCircularQueueDeQueue(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)) return false;//obj->a[obj->k] = -1; 无需通过人为干预,赋值覆盖原值已经能够相当于元素从队列中被剔除obj->head == obj->k ? obj->head = 0 : obj->head ++;return true;
}int myCircularQueueFront(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)) return -1;return obj->a[obj->head];
}int myCircularQueueRear(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)) return -1;return obj->tail == 0 ? obj->a[obj->k] : obj->a[obj->tail-1];
}void myCircularQueueFree(MyCircularQueue* obj) {free(obj->a);obj->k = obj->head = obj->tail = 0;
}/*** Your MyCircularQueue struct will be instantiated and called as such:* MyCircularQueue* obj = myCircularQueueCreate(k);* bool param_1 = myCircularQueueEnQueue(obj, value);* bool param_2 = myCircularQueueDeQueue(obj);* int param_3 = myCircularQueueFront(obj);* int param_4 = myCircularQueueRear(obj);* bool param_5 = myCircularQueueIsEmpty(obj);* bool param_6 = myCircularQueueIsFull(obj);* myCircularQueueFree(obj);
*/