深度解析大模型学习率：优化策略与挑战

大模型超参数Learning Rate的深度学习

学习率（Learning Rate）是机器学习和深度学习中最核心的超参数之一，尤其在训练大规模语言模型（LLMs）时，其设置直接影响模型的收敛速度、训练稳定性及最终性能。以下从多维度详细解析学习率的定义、作用、挑战及优化策略。

---

一、学习率的基本定义与作用

1. 数学定义
   学习率（记为$\alpha$）是梯度下降优化算法中控制参数更新步长的系数。参数更新公式为：
   $${\theta }_{t+1}={\theta }_t-\alpha \cdot {\nabla }_{\theta }L({\theta }_t)$$
   其中，${\nabla }_{\theta }L({\theta }_t)$是损失函数对参数的梯度，$\alpha$决定了每次迭代中参数调整的幅度。

2. 核心作用

   • 收敛速度：较大的学习率加快收敛，但可能导致震荡或不收敛；较小的学习率收敛稳定但速度慢。
   • 解的质量：合适的学习率帮助模型跳出局部最优，接近全局最优；反之可能导致欠拟合或过拟合。
   • 训练稳定性：极端学习率可能引发梯度爆炸（过大）或梯度消失（过小）。

3. 典型影响示例

   • 过高学习率：损失函数快速下降后剧烈波动，甚至出现NaN（梯度爆炸）。
     
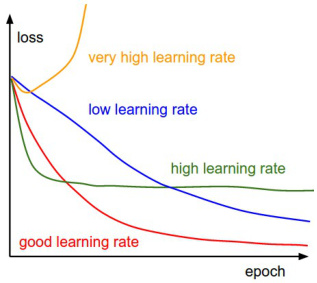
   • 过低学习率：损失下降缓慢，训练时间显著增加，可能陷入局部最优。

---

二、大模型训练中学习率的关键挑战

1. 梯度噪声与批量大小的权衡
   大模型通常采用大批量训练以提升计算效率，但批量增大后梯度噪声降低，需调整学习率以保持更新有效性。研究表明，批量大小（Batch Siz