数据结构实验9.2：动态查找表的基本操作

---

一，实验目的

1. 熟练掌握各种静态查找表方法（顺序查找、折半查找、索引顺序表等）：通过对不同静态查找表方法的实践操作，深入理解其原理、实现过程和适用场景，能够根据实际需求灵活选择合适的查找方法，提高数据查找的效率和准确性。
2. 熟练掌握二叉排序树的构造方法、插入算法、删除算法和查找算法：全面深入地了解二叉排序树的特性，精准把握其节点的插入、删除和查找逻辑，能够熟练运用这些算法构建和操作二叉排序树，为解决复杂的数据存储和检索问题提供有力支持。
3. 掌握散列表的有关技术及各种基本运算的算法：透彻理解散列函数的设计、散列表的存储结构以及冲突处理方法，熟练实现散列表的插入、查找、删除等基本运算，能够根据数据特点合理设计散列表，提高数据处理的效率。

二，实验内容

已知有一个关键字序列（40，20，10，80，98，8，50，5，70），完成基于该序列的下列二叉排序树的基本操作。

（1）从一棵空二叉树开始，每输入一个元素，就建立一个新结点并插入到当前已生成的二叉排序树中，完成二叉排序树的建立

按照给定的关键字序列顺序，依次将每个关键字作为新节点插入到初始为空的二叉排序树中。依据二叉排序树的性质，若新节点的关键字小于当前节点的关键字，则插入到当前节点的左子树；若大于当前节点的关键字，则插入到当前节点的右子树。通过这样的方式逐步构建出完整的二叉排序树。

（2）完成二叉排序树的插入和删除操作

• 插入操作：对于给定的关键字，先在二叉排序树中查找是否已存在相同关键字的节点。若不存在，则根据二叉排序树的规则确定插入位置并插入新节点；若存在，则插入失败。
• 删除操作：首先在二叉排序树中查找要删除的节点。若该节点是叶子节点，直接删除；若节点只有左子树或右子树，将其左子树或右子树直接连接到其父节点；若节点既有左子树又有右子树，则在其左子树中找到最大节点（或在右子树中找到最小节点），将该节点的值赋给要删除的节点，然后删除这个替代节点。

（3）完成二叉排序树的查找操作，返回查找是否成功

从二叉排序树的根节点开始，将待查找的关键字与当前节点的关键字进行比较。若相等，则查找成功，返回指向该节点的指针；若小于当前节点的关键字，则继续在左子树中查找；若大于当前节点的关键字，则继续在右子树中查找。若遍历完整个二叉排序树都未找到相等的关键字，则查找失败，返回 NULL。

（4）对二叉排序树进行中序遍历，输出中序遍历序列

按照中序遍历的规则，先递归遍历左子树，然后访问根节点，最后递归遍历右子树。在遍历过程中，依次输出节点的关键字，最终得到二叉排序树的中序遍历序列。中序遍历二叉排序树得到的序列是一个有序序列，这也是二叉排序树的重要特性之一。

三，实验要求

（1）设计二叉排序树的链式存储结构

定义二叉排序树的节点结构体，包含数据域（存储关键字及其他相关信息）和两个指针域（分别指向左子树和右子树）。例如：

typedef struct BiTnode{TElemType data;        //数据域，存储关键字等信息struct BiTnode *lchild, *rchild;   //指针域，分别指向左、右子树
} BiTnode, *BiTree;

（2）进行算法分析与设计

• 时间复杂度分析：插入算法在最坏情况下需要遍历从根节点到叶子节点的路径，时间复杂度为 $O(h)$，其中 $h$ 为二叉排序树的高度。查找算法同理，在最坏情况下时间复杂度也为 $O(h)$。对于删除算法，若删除节点后调整树结构的操作较为复杂，时间复杂度也可能达到 $O(h)$。在平衡的二叉排序树中，$h={\log }_{2}n$（$n$ 为节点个数），但在最坏情况下（如退化为链表的二叉排序树），$h=n$。
• 空间复杂度分析：这些算法主要的空间开销在于递归调用栈（在递归实现的情况下）以及存储二叉排序树节点本身。一般情况下，空间复杂度为 $O(h)$，用于存储递归调用过程中的状态等信息。

（3）仔细阅读并掌握参考程序中的各种算法，在参考程序中的下划线处填上适当的语句或文字

认真研读参考程序中插入、查找等算法的代码逻辑，明确每个变量和语句的作用。根据算法的执行流程和功能需求，在空缺处准确填写相应的语句或文字，确保程序的逻辑完整性和正确性。例如，检查插入算法中对特殊情况（如空树插入）的处理是否完整，查找算法中对返回值的处理是否准确等。

（4）上机调试、测试参考程序，打印测试结果，对测试结果进行分析

使用不同的测试数据对参考程序进行全面测试，包括正常数据（如给定的关键字序列）、边界数据（如查找树中最小或最大关键字、插入重复关键字等情况）以及异常数据（如空树的操作等）。记录程序的运行结果，观察插入、删除、查找操作是否正确执行，中序遍历序列是否符合预期。对测试结果进行深入分析，总结算法在不同情况下的性能表现，如插入操作的效率、查找操作的准确性等，分析可能存在的问题和改进方向。

四，算法分析

（一）插入算法设计

Status InsertBST(BiTree &T, TElemType e) {//当二叉排序树中不存在关键字等于e.key的数据元素时，//插入元素e并返回true，否则返回falseBiTree p = T; BiTree parent = NULL;		// 用p控制循环，parent指向p的父结点while (p && p->data.key!= e.key) {parent = p;if (e.key > p->data.key) p = p->rchild;else p = p->lchild;}//whileif (p) return false;  		// 键值为e.key的结点已经存在，插入失败！BiTree s = new BiTnode;			// 准备新结点s->data = e;   s->lchild = s->rchild = NULL;if (parent == NULL)  T = s;	// 插入else if (e.key > parent->data.key) parent->rchild = s;else parent->lchild = s;	// 新结点作为parent的孩子插入到BST中return true;
}//InsertBST 

分析：该算法首先从根节点开始，使用 p 指针在二叉排序树中查找关键字为 e.key 的节点。在查找过程中，parent 指针始终记录 p 的父节点。如果找到关键字相等的节点（p 不为 NULL），说明该关键字已存在，直接返回 false 表示插入失败。若未找到（p 为 NULL），则创建新节点 s，并根据 parent 是否为 NULL 判断是否为根节点插入。若 parent 不为 NULL，再根据 e.key 与 parent->data.key 的大小关系，将新节点插入到 parent 的左子树或右子树。此算法的时间复杂度在平均情况下为 $O({\log }_{2}n)$，其中 $n$ 为二叉排序树的节点个数，但在最坏情况下（如二叉排序树退化为链表），时间复杂度会达到 $O(n)$。空间复杂度主要为创建新节点的开销，为 $O(1)$。

（二）查找算法设计

BiTree SearchBST(BiTree T, KeyType key) {//在T指向根的二叉排序树中查找关键字等于key的数据//元素，若找到，返回指向该结点的指针，否则返回null BiTree p = T;while (p!= NULL) {if (key == p->data.key)  return p;if (key < p->data.key)  p = p->lchild;else  p = p->rchild; }return NULL; 
}

分析：算法从根节点 T 开始，使用 p 指针在二叉排序树中进行查找。每次将 p 指向的节点关键字与待查找的 key 进行比较。若相等，则找到了目标节点，返回该节点的指针。若 key 小于 p->data.key，则继续在 p 的左子树中查找；若 key 大于 p->data.key，则继续在 p 的右子树中查找。当 p 为 NULL 时，说明遍历完整个树都未找到目标节点，返回 NULL 表示查找失败。该算法的时间复杂度在平均情况下为 $O({\log }_{2}n)$，最坏情况下为 $O(n)$，空间复杂度为 $O(1)$，因为仅使用了少量辅助变量来控制查找过程。

五，示例代码

9-2.cpp源代码

#define TRUE 1
#define FALSE 0
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>typedef int Status;
typedef int TElemType;typedef struct BiTnode {TElemType      data;               //数据域struct BiTnode* lchild, * rchild;   //指针域
} BiTnode, * BiTree;Status InsertBST(BiTree& T, TElemType e) {//当二叉排序树中不存在关键字等于e的数据元素时，//插入元素e并返回true，否则返回falseBiTree p, parent, s;   // parent指针始终指向p的父结点p = T; parent = NULL;while (p && p->data != e) {    //定位插入点parent = p;if (e > p->data)p = p->rchild;        // 如果插入值大于当前节点值，向右子树移动elsep = p->lchild;        // 如果插入值小于当前节点值，向左子树移动}if (p) return FALSE;   //键值为e的结点已经存在s = new BiTnode;s->data = e;   s->lchild = s->rchild = NULL;if (!parent)  T = s;    //若树空，则新结点作为根结点else if (e > parent->data) parent->rchild = s;   //判断插左还是插右else parent->lchild = s;return TRUE;
}BiTree SearchBST(BiTree T, TElemType key) {//在T指向根的二叉排序树中查找关键字等于key的数据//元素，若找到，返回指向该结点的指针，否则返回null BiTree p = T;printf("  查找路径==>");while (p && p->data != key) {   // 若当前结点不是要找的结点则循环printf("%4d", p->data);if (key < p->data)  p = p->lchild;   // 如果查找值小于当前节点值，向左子树移动else  p = p->rchild;}if (p)  printf("%4d", p->data);return p;
}Status Delete(BiTree& p)
{BiTree q, s;if (!p->rchild) {     //右子树空，则只需重接它的左子树q = p;p = p->lchild;free(q);}else if (!p->lchild) {  // 左子树空， 则只需重接它的右子树q = p;p = p->rchild;free(q);}else {                // 左右子树均不空q = p;  s = p->lchild;while (s->rchild) {q = s;  s = s->rchild;}p->data = s->data;if (q != p)  q->rchild = s->lchild;else  q->lchild = s->lchild;free(s);}return TRUE;
}Status Del_BST(BiTree& T, TElemType e)     // 删除结点
{if (!T) return FALSE;else {if (T->data == e) return Delete(T);else if (T->data > e) return Del_BST(T->lchild, e);else return Del_BST(T->rchild, e);}
}void InorderBST(BiTree T) {       // 中序遍历if (T != NULL){InorderBST(T->lchild);printf("%4d", T->data);InorderBST(T->rchild);}
}void OutputBST(BiTree T)                        // 二叉排序树输出
{       // 先序递归遍历方式输出括号表示的二叉排序树if (T != NULL)                              // 终止项{printf("%d", T->data);                   // 访问根结点if (T->lchild != NULL || T->rchild != NULL){printf("(");                        // 根的孩子用圆括号对括OutputBST(T->lchild);               // 先序遍历输出左子树if (T->rchild != NULL)printf(",");                    // 根的左右孩子以“，”分隔OutputBST(T->rchild);               // 先序遍历输出右子树printf(")");                        // 根的孩子用圆括号对括}}
}int main() {                                //  主函数。BiTree  p, bt = NULL;int k;printf("===========二叉排序树的基本操作============\n");printf("(1)插入新结点......\n");while (1){printf("  输入新增结点键值(-1结束)：");scanf("%d", &k);if (k == -1) {printf("  插入结束！二叉排序树输出：");OutputBST(bt);printf("\n  中序遍历序列输出：");if (bt) {InorderBST(bt);printf("\n");}elseprintf("空\n");break;}if (!InsertBST(bt, k))printf("  该键值已经存在！请重新输入！\n");}printf("(2)删除结点......\n");while (1){printf("  请输入被删结点键值(-1结束)：");scanf("%d", &k);if (k == -1) break;if (!Del_BST(bt, k))printf("  该键值不存在，请重新输入！\n");else {printf("  删除成功！当前二叉排序树输出：");OutputBST(bt);printf("\n  中序遍历序列输出：");if (bt) {InorderBST(bt);printf("\n");}elseprintf("空\n");break;}}printf("(3)查找结点......\n");while (1){printf("  输入待查找结点的键值(-1结束)：");scanf("%d", &k);if (k == -1) break;p = SearchBST(bt, k);if (p)printf("  查找成功！结点的键值是：%d\n", p->data);elseprintf("  查找失败！\n");}return 0;
}

六，操作步骤

1，双击Visual Studio程序快捷图标，启动程序。

2，之前创建过项目的话，直接打开即可，这里选择【创建新项目】。

3，单击选择【空项目】——单击【下一步】按钮。

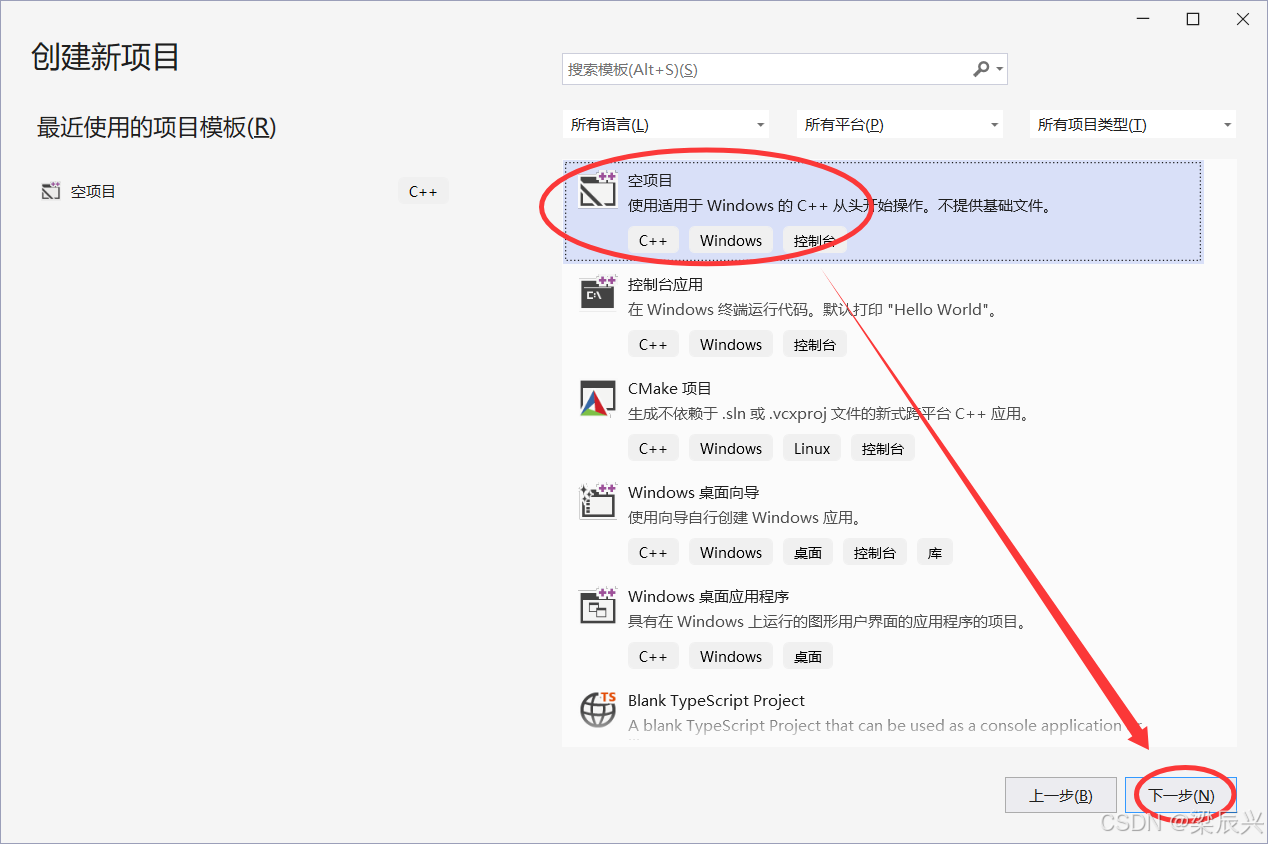
4，编辑好项目的名称和存放路径，然后单击【创建】按钮。

5，创建C++程序文件，右击【源文件】——选择【添加】——【新建项】。

6，输入项目名称9-2.cpp，单击【添加】按钮。

7，编写代码，单击运行按钮，运行程序。

七，运行结果

1，实验要求的测试结果。

2，编写代码测试测试的结果。