当前位置：首页 > news >正文

单因子实验方差分析

news 来源：原创 2025/5/11 13:10:10

本文是实验设计与分析（第6版，Montgomery著傅珏生译)第3章单因子实验方差分析python解决方案。本文尽量避免重复书中的理论，着于提供python解决方案，并与原书的运算结果进行对比。您可以从下载实验设计与分析（第6版，Montgomery著傅珏生译)电子版。本文假定您已具备python基础，如果您还没有python的基础，可以从

下载相关资料进行学习。

3.1一个例子

在集成电路的许多生产步骤中，晶片被一层材料（如二氧化硅或某种金属）完全覆盖。通过对掩模的蚀刻有选择性地除去不需要的材料，从而创建电路模板、电互连以及必须扩散的或者金属沉积的区域。等离子蚀刻工序在这个操作中被广泛使用，特别是在几何对象比较小的情况下的应用。图3.1展示了一种典型的单晶片蚀刻设备的重要特征。射频（RF）发生器提供能源，使得电极之间的间隙产生等离子。等离子体的化学种类是由所使用的特定气体决定的。碳氟化合物，

比如CF4（四氟甲烷）或C2F6（六氟乙烷），通常被用在等离子蚀刻上。但是根据应用情况的不同，也常使用其他的气体或混合气体.

工程师要研究这套设备的RF功率设置与蚀刻率间的关系。实验目的是建立蚀刻率与RF功率之间关系的模型，以确定达到所需的目标蚀刻率的功率设置。她选定了气体（C2F。）和间限（0.80cm），想检验RF功率的4个水平：160W，180W，200W和220W.她决定在RF功率的每个水平上检验5个晶片。

这是一个因子水平a=4和重复n=5的单因子实验。这20个试验都是按照随机次序进行的。一种生成随机次序的更高效方法是将20个试验输入电子表格（Excel），用Rand（）函数产生一列随机数，以此排序。

假设从这个过程中获得的试验次序是

为防止未知讨厌变量的影响，随机化试验次序是必要的。因为实验中讨厌变量的变化也许会超出控制范围，从而损害实验结果。为了说明这一点，假定我们按原始的非随机化次序做20个晶片试验（也就是，前5个功率用160W，接下来的5个功率用180W，依次类推）。如果蚀刻设备有热身效应，则运行越长，观测的蚀刻率读数就越低，热身效应将潜在地损害数据，从而破坏实验的有效性。

假定工程师按照我们确定的随机次序进行试验.得到的蚀刻率的观测值如表3.1所示

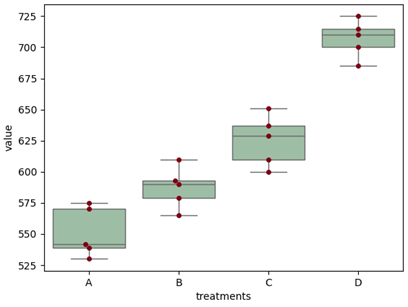
用图示方法来检查实验数据的想法也很好.图3.2（盒图）展示了RF功率的每个水平的蚀刻率，图3.2b是蚀刻率关于RF功率的散点留.两类图都表明蚀刻率随着功率设置的增加而增加，但没有明显证据表明蚀刻率相对于均值的变异性依赖于功率设置.基于这个简单的图形分析，我们猜想：（1）F功率设置影响蚀刻率；（2）功率设置提高时，蚀刻率增加。

假定想更客观地分析这些数据。特别地，假定希望检验在RF功率的所有α=4水平下蚀刻率均值间的差异。于是，我们想要检验所有的4个均值是否都相等，粗看起来，这个问题可以用所有6个可能的配对比较的t检验来解决。但是，这并不是解决这个问题的最好方法。首先，做6个t检验效率很低，事倍功半。第二，这些配对比较的执行增大了第一类误差。假定4个均值都相等，如果我们选择a=0.05，则在每一单个比较上作出正确决策的概率是0.95.但是，所有6个比较都是正确决策的概率就远远小于0.95，所以，第一类错误被增大了。

方差分析是检验若干个均值相等的比较好的方法。不过，方差分析的用途比解决上述问题要更为广泛得多。它可能是在统计推断领域中最有用的方法。

# 将以下数据保存为anovaoneway.txt

A B C D

575 565 600 725

542 593 651 700

530 590 610 715

539 579 637 685

570 610 629 710

#以下为p.50/56/57 表3.1 图3.2（b）pyhthon代码，与"anovaoneway.txt"放在同一目录下

import pandas as pd

# load data file

df = pd.read_csv("anovaoneway.txt", sep="\t")

>>> df

A B C D

0 575 565 600 725

1 542 593 651 700

2 530 590 610 715

3 539 579 637 685

4 570 610 629 710

# reshape the d dataframe suitable for statsmodels package

df_melt = pd.melt(df.reset_index(), id_vars=['index'], value_vars=['A', 'B', 'C', 'D'])

# replace column names

df_melt.columns = ['index', 'treatments', 'value']

# generate a boxplot to see the data distribution by treatments. Using boxplot, we can

# easily detect the differences between different treatments

>>> df['A'].mean()

551.2

>>> df['B'].mean()

587.4

>>> df['C'].mean()

625.4

>>> df['D'].mean()

707.0

>>> df.mean()

A    551.2

B    587.4

C    625.4

D    707.0

dtype: float64

import matplotlib.pyplot as plt

import seaborn as sns

ax = sns.boxplot(x='treatments', y='value', data=df_melt, color='#99c2a2')

ax = sns.swarmplot(x="treatments", y="value", data=df_melt, color='#7d0013')

plt.show()

3.2 方差分析（略，本部分为理论内容，见原书）

3.3固定效应模型的分析

3.3.1总平方和的分解（略，本部分为理论内容，见原书）

3.3.2统计分析

例3，1晶片蚀刻实验

为说明方差分析方法，我们回到3.1节讨论过的例子。开发工程师要确定RF功率设置是否影响蚀刻率，她进行了RF功率有4个水平和5次重复的完全随机化实验。为方便起见，此处重复表3.1的数据如下

我们用方差分析检验原假设H0:μ1=μ2=μ3=μ4与备择假设H1:部分均值不等。用（3.8）式、（3.9）式和（3.10）式计算所需的平方和如下：

通常，这些计算是通过使用具有分析从已设计的实验中获得的数据的能力的软件包在计算机上进行的。

方差分析概括在表3.4中。RF功率或处理间的均方值（22290.18）是处理内部或误差均方值（333.70）的好几倍。这表明处理均值都相等是不大可能的。形式上，计算F的比值F0=22290.18/333.70=66.80，并与分布F3，16合适的上尾百分点比较。假定实验者选择a=0.05，从附表VI我们发现F0.05.3，16=3.24，因为F0=66.80>3.24，所以我们拒绝H0，并得出处里均值不相同的结论。也就是说，RF功率的设置对平均蚀刻率有显著影响。我们还可以计算检验统计量的P值。图3，3给出了检验统计量F0的参考分布（F3，16）。显然，本例中P值非常小。因为F0.01，3.16=5.29且F0>5.29，所以可以得出结论：P值的一个上界为0.01，即P<0.01（精确P值为P=2.88×10-9）。