Python训练打卡Day17
无监督算法中的聚类
知识点
- 聚类的指标
- 聚类常见算法:kmeans聚类、dbscan聚类、层次聚类
- 三种算法对应的流程
实际在论文中聚类的策略不一定是针对所有特征,可以针对其中几个可以解释的特征进行聚类,得到聚类后的类别,这样后续进行解释也更加符合逻辑。
聚类的流程
- 标准化数据
- 选择合适的算法,根据评估指标调参( )
- 将聚类后的特征添加到原数据中
- 原则t-sne或者pca进行2D或3D可视化
KMeans 和层次聚类的参数是K值,选完k指标就确定DBSCAN 的参数是 eps 和min_samples,选完他们出现k和评估指标
以及层次聚类的 linkage准则等都需要仔细调优。
除了经典的评估指标,还需要关注聚类出来每个簇对应的样本个数,避免太少没有意义。
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import seaborn as sns# 标准化数据(聚类前通常需要标准化)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# X_scaled#聚类评估指标
1.轮廓系数(Silhouette Score)
定义:轮廓系数衡量每个样本与其所属簇的紧密程度以及与最近其他簇的分离程度。
取值范围:轮廓系数越接近1,表示样本与其所属簇内其他样本很近,与其他簇很远,聚类效果越好。轮廓系数越接近-1,表示样本与其所属簇内样本较远,与其他簇较近,聚类效果越差(可能被错误分类)。轮廓系数接近 0,表示样本在簇边界附近,聚类效果无明显好坏。
选择轮廓系数最高的 `k` 值作为最佳簇数量
2. CH 指数 (Calinski-Harabasz Index)
定义:CH 指数是簇间分散度与簇内分散度之比,用于评估簇的分离度和紧凑度。
取值范围:CH 指数越大,表示簇间分离度越高,簇内紧凑度越高,聚类效果越好。没有固定的上限,值越大越好。选择 CH 指数最高的 `k` 值作为最佳簇数量。
3. DB 指数 (Davies-Bouldin Index)
定义:DB 指数衡量簇间距离与簇内分散度的比值,用于评估簇的分离度和紧凑度
取值范围:DB 指数越小,表示簇间分离度越高,簇内紧凑度越高,聚类效果越好。没有固定的上限,值越小越好。选择 DB 指数最低的 `k` 值作为最佳簇数量。
轮廓系数:可以比喻为一个人在聚会中,和同组的人是否亲近,而与其他组的人是否疏远。如果这个人在自己组里很合群,且离其他组的人很远,那么他的轮廓系数就高,说明分组合理。
CH指数:可以用班级之间的比较。比如,每个班级内部的学生成绩比较接近(紧凑),而不同班级之间的平均成绩差异较大(分离),这样CH指数就高,说明分班效果好。
DB指数:可以想象成不同岛屿之间的距离和
K-means算法
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 k 值下的指标
k_range = range(2, 11) # 测试 k 从 2 到 10
inertia_values = []
silhouette_scores = []
ch_scores = []
db_scores = []for k in k_range:kmeans = KMeans(n_clusters=k, random_state=42)kmeans_labels = kmeans.fit_predict(X_scaled)inertia_values.append(kmeans.inertia_) # 惯性(肘部法则)silhouette = silhouette_score(X_scaled, kmeans_labels) # 轮廓系数silhouette_scores.append(silhouette)ch = calinski_harabasz_score(X_scaled, kmeans_labels) # CH 指数ch_scores.append(ch)db = davies_bouldin_score(X_scaled, kmeans_labels) # DB 指数db_scores.append(db)print(f"k={k}, 惯性: {kmeans.inertia_:.2f}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")# 绘制评估指标图
plt.figure(figsize=(15, 10))# 肘部法则图(Inertia)
plt.subplot(2, 2, 1)
plt.plot(k_range, inertia_values, marker='o')
plt.title('肘部法则确定最优聚类数 k(惯性,越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('惯性')
plt.grid(True)# 轮廓系数图
plt.subplot(2, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o', color='orange')
plt.title('轮廓系数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('轮廓系数')
plt.grid(True)# CH 指数图
plt.subplot(2, 2, 3)
plt.plot(k_range, ch_scores, marker='o', color='green')
plt.title('Calinski-Harabasz 指数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('CH 指数')
plt.grid(True)# DB 指数图
plt.subplot(2, 2, 4)
plt.plot(k_range, db_scores, marker='o', color='red')
plt.title('Davies-Bouldin 指数确定最优聚类数 k(越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()
1. 肘部法则图: 找下降速率变慢的拐点,这里都差不多
2. 轮廓系数图:找局部最高点,这里选6不能选7
3. CH指数图: 找局部最高点,这里选7之前的都还行
4. DB指数图:找局部最低点,这里选6 7 9 10都行
综上,选择6比较合适。
# 提示用户选择 k 值
selected_k = 6# 使用选择的 k 值进行 KMeans 聚类
kmeans = KMeans(n_clusters=selected_k, random_state=42)
kmeans_labels = kmeans.fit_predict(X_scaled)
X['KMeans_Cluster'] = kmeans_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# KMeans 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=kmeans_labels, palette='viridis')
plt.title(f'KMeans Clustering with k={selected_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 KMeans 聚类标签的前几行
print(f"KMeans Cluster labels (k={selected_k}) added to X:")
print(X[['KMeans_Cluster']].value_counts())
DBCSAN聚类算法
import numpy as np
import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 eps 和 min_samples 下的指标
# eps这个参数表示邻域的半径,min_samples表示一个点被认为是核心点所需的最小样本数。
# min_samples这个参数表示一个核心点所需的最小样本数。eps_range = np.arange(0.3, 0.8, 0.1) # 测试 eps 从 0.3 到 0.7
min_samples_range = range(3, 8) # 测试 min_samples 从 3 到 7
results = []for eps in eps_range:for min_samples in min_samples_range:dbscan = DBSCAN(eps=eps, min_samples=min_samples)dbscan_labels = dbscan.fit_predict(X_scaled)# 计算簇的数量(排除噪声点 -1)n_clusters = len(np.unique(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)# 计算噪声点数量n_noise = list(dbscan_labels).count(-1)# 只有当簇数量大于 1 且有有效簇时才计算评估指标if n_clusters > 1:# 排除噪声点后计算评估指标mask = dbscan_labels != -1if mask.sum() > 0: # 确保有非噪声点silhouette = silhouette_score(X_scaled[mask], dbscan_labels[mask])ch = calinski_harabasz_score(X_scaled[mask], dbscan_labels[mask])db = davies_bouldin_score(X_scaled[mask], dbscan_labels[mask])results.append({'eps': eps,'min_samples': min_samples,'n_clusters': n_clusters,'n_noise': n_noise,'silhouette': silhouette,'ch_score': ch,'db_score': db})print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, "f"轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")else:print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, 无法计算评估指标")# 将结果转为 DataFrame 以便可视化和选择参数
results_df = pd.DataFrame(results)results_df# 绘制评估指标图,增加点论文中的工作量
plt.figure(figsize=(15, 10))
# 轮廓系数图
plt.subplot(2, 2, 1)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples] # plt.plot(subset['eps'], subset['silhouette'], marker='o', label=f'min_samples={min_samples}')
plt.title('轮廓系数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('轮廓系数')
plt.legend()
plt.grid(True)# CH 指数图
plt.subplot(2, 2, 2)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['ch_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Calinski-Harabasz 指数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('CH 指数')
plt.legend()
plt.grid(True)# DB 指数图
plt.subplot(2, 2, 3)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['db_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Davies-Bouldin 指数确定最优参数(越小越好)')
plt.xlabel('eps')
plt.ylabel('DB 指数')
plt.legend()
plt.grid(True)# 簇数量图
plt.subplot(2, 2, 4)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['n_clusters'], marker='o', label=f'min_samples={min_samples}')
plt.title('簇数量变化')
plt.xlabel('eps')
plt.ylabel('簇数量')
plt.legend()
plt.grid(True)plt.tight_layout()
plt.show()
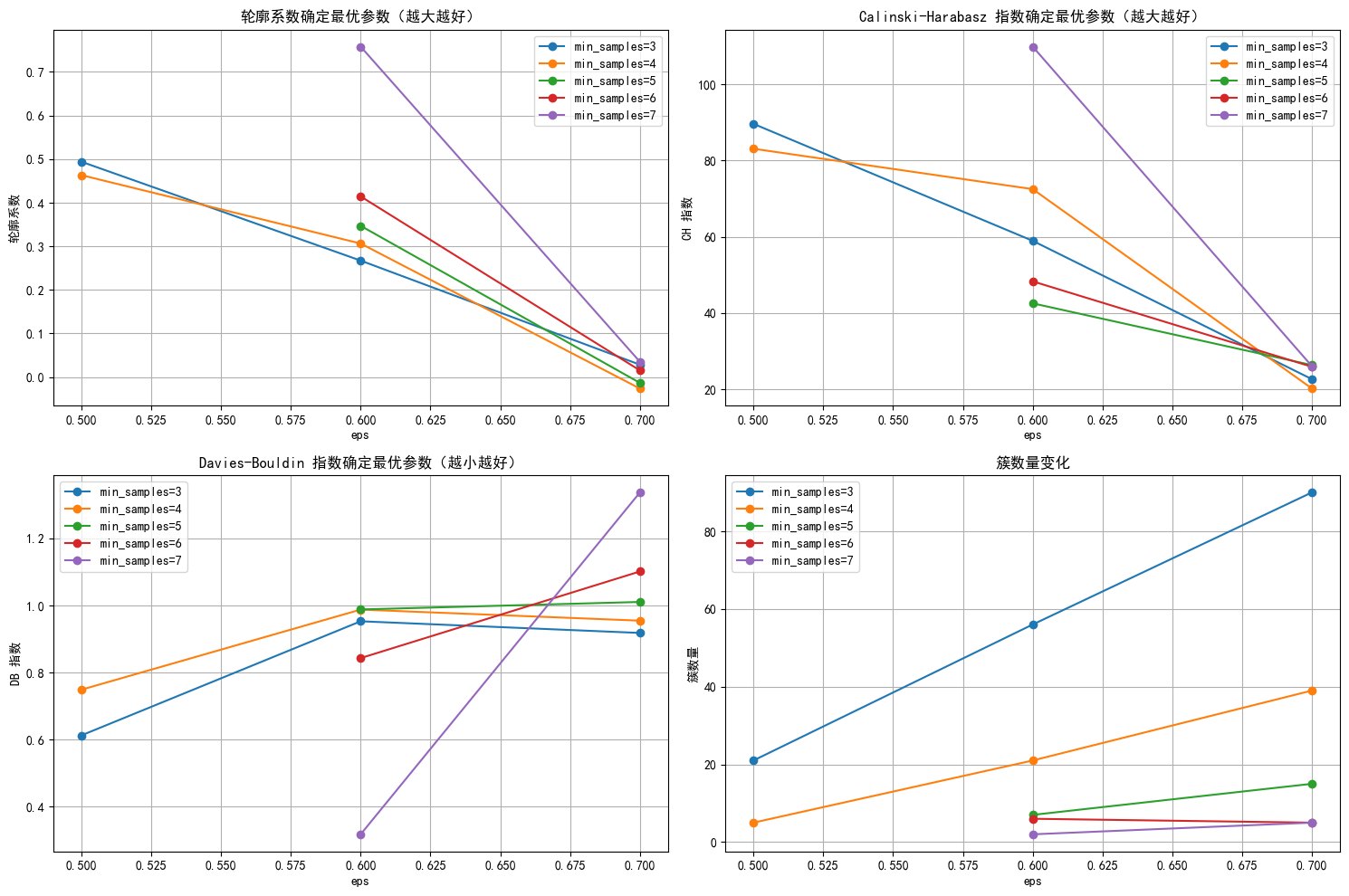
# 选择 eps 和 min_samples 值(根据图表选择最佳参数)
selected_eps = 0.6 # 根据图表调整
selected_min_samples = 6 # 根据图表调整# 使用选择的参数进行 DBSCAN 聚类
dbscan = DBSCAN(eps=selected_eps, min_samples=selected_min_samples)
dbscan_labels = dbscan.fit_predict(X_scaled)
X['DBSCAN_Cluster'] = dbscan_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# DBSCAN 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=dbscan_labels, palette='viridis')
plt.title(f'DBSCAN Clustering with eps={selected_eps}, min_samples={selected_min_samples} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 DBSCAN 聚类标签的分布
print(f"DBSCAN Cluster labels (eps={selected_eps}, min_samples={selected_min_samples}) added to X:")
print(X[['DBSCAN_Cluster']].value_counts())
根据代码运行结果可以判断算法合不合适。
层次聚类
import numpy as np
import pandas as pd
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 评估不同 n_clusters 下的指标
n_clusters_range = range(2, 11) # 测试簇数量从 2 到 10
silhouette_scores = []
ch_scores = []
db_scores = []for n_clusters in n_clusters_range:agglo = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward') # 使用 Ward 准则合并簇agglo_labels = agglo.fit_predict(X_scaled)# 计算评估指标silhouette = silhouette_score(X_scaled, agglo_labels)ch = calinski_harabasz_score(X_scaled, agglo_labels)db = davies_bouldin_score(X_scaled, agglo_labels)silhouette_scores.append(silhouette)ch_scores.append(ch)db_scores.append(db)print(f"n_clusters={n_clusters}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")# 绘制评估指标图
plt.figure(figsize=(15, 5))# 轮廓系数图
plt.subplot(1, 3, 1)
plt.plot(n_clusters_range, silhouette_scores, marker='o')
plt.title('轮廓系数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('轮廓系数')
plt.grid(True)# CH 指数图
plt.subplot(1, 3, 2)
plt.plot(n_clusters_range, ch_scores, marker='o')
plt.title('Calinski-Harabasz 指数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('CH 指数')
plt.grid(True)# DB 指数图
plt.subplot(1, 3, 3)
plt.plot(n_clusters_range, db_scores, marker='o')
plt.title('Davies-Bouldin 指数确定最优簇数(越小越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()
# 提示用户选择 n_clusters 值(这里可以根据图表选择最佳簇数)
selected_n_clusters = 10 # 示例值,根据图表调整# 使用选择的簇数进行 Agglomerative Clustering 聚类
agglo = AgglomerativeClustering(n_clusters=selected_n_clusters, linkage='ward')
agglo_labels = agglo.fit_predict(X_scaled)
X['Agglo_Cluster'] = agglo_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# Agglomerative Clustering 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=agglo_labels, palette='viridis')
plt.title(f'Agglomerative Clustering with n_clusters={selected_n_clusters} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 Agglomerative Clustering 聚类标签的分布
print(f"Agglomerative Cluster labels (n_clusters={selected_n_clusters}) added to X:")
print(X[['Agglo_Cluster']].value_counts())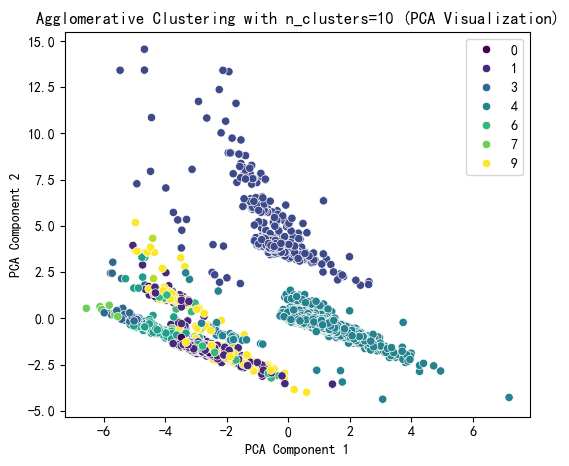
# 层次聚类的树状图可视化
from scipy.cluster import hierarchy
import matplotlib.pyplot as plt# 假设 X_scaled 是标准化后的数据
# 计算层次聚类的链接矩阵
Z = hierarchy.linkage(X_scaled, method='ward') # 'ward' 是常用的合并准则# 绘制树状图
plt.figure(figsize=(10, 6))
hierarchy.dendrogram(Z, truncate_mode='level', p=3) # p 控制显示的层次深度
# hierarchy.dendrogram(Z, truncate_mode='level') # 不用p这个参数,可以显示全部的深度
plt.title('Dendrogram for Agglomerative Clustering')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.show()
1. 横坐标代表每个簇对应样本的数据,这些样本数目加一起是整个数据集的样本数目。这是从上到下进行截断,p=3显示最后3层,不用p这个参数会显示全部。
2. 纵轴代表距离 ,反映了在聚类过程中,不同样本或簇合并时的距离度量值。距离越大,意味着两个样本或簇之间的差异越大;距离越小,则差异越小。
总结:
1. 聚类算法的原理
- 核心思想:把相似的东西分到同一组,不相似的隔开,不需要提前知道分组规则(无监督学习)。
- 生活比喻:
- 图书馆整理书籍:没有标签分类,管理员根据书名、主题自动把相似的书放在同一书架。
- 超市整理货架:把饮料、零食、日用品分开摆放,顾客一眼能找到同类商品。
- 关键问题:
- 什么是“相似”?→ 用距离(如欧氏距离)或密度衡量。
- 分多少组?→ 有些算法需指定组数(如K-means),有些自动判断(如DBSCAN)。
2. K-means算法
- 核心思想:“物以类聚,人以群分”,先随便画几个圈,不断调整圈的位置,直到圈内人最亲密。
- 通俗比喻:
- 披萨店分区:老板想给不同区域的客人送不同口味的披萨。
- 随机选几个中心点(比如东区、西区、南区)。
- 每个客人选择离自己最近的中心点,形成临时分组。
- 根据每个组的客人位置,重新计算中心点(比如东区客人往北移了,中心点也北移)。
- 重复调整,直到中心点不再变化。
- 披萨店分区:老板想给不同区域的客人送不同口味的披萨。
- 优缺点:
- ✅ 简单高效,适合均匀分布的球形数据。
- ❌ 要提前指定分组数(K值),对异常值敏感(比如有个客人住在荒郊野外,影响中心点)。
3. DBSCAN算法
- 核心思想:“抱团取暖,远离孤岛”,通过密度找核心人群,边缘和孤立的点直接忽略。
- 通俗比喻:
- 岛屿探险:
- 核心点:人群密集的岛屿(周围有足够多的邻居)。
- 边界点:住在岛屿边缘的人(依赖核心点存在)。
- 噪声点:海上孤零零的漂流者(没人搭理)。
- 规则:从一个核心点出发,把周围可达的邻居(包括其他核心点)拉进同一群岛。
- 岛屿探险:
- 优缺点:
- ✅ 能发现任意形状的簇(比如长条形的河流居民区),自动过滤噪声。
- ❌ 对密度参数敏感(比如“多少人才算密集?”需要手动调参)。
4. 层次聚类
- 核心思想:“合并小团体,形成大组织”,像搭积木一样逐层构建分组关系。
- 通俗比喻:
- 自底向上(聚合式):
- 每个人自成一组。
- 找距离最近的两个组合并(比如张三和李四)。
- 重复合并,直到所有人在一个大组。
结果形成“树状图”(类似家族族谱)。
- 自顶向下(分裂式):
- 所有人先在一个大组。
- 不断分裂成更小的组,直到每人单独一组。
- 自底向上(聚合式):
- 优缺点:
- ✅ 不需要指定分组数,可视化直观(树状图)。
- ❌ 计算量大(数据多时很慢),一旦合并/分裂不可逆。
@浙大疏锦行
