第2章 神经网络的数学基础
本章我们将梳理一下神经网络所需的数学基础知识,其中大多数内容没有超出高中所学范围,因此读起来不会吃力。
2-1神经网络所需的函数
本节我们来看一下神经网络世界中频繁出现的函数。虽然它们都是基本的函数,但是对于神经网络是不可缺少的。
一次函数
在数学函数中最基本、最重要的就是一次函数。它在神经网络的世界里也同样重要。这个函数可以用下式表示。
y=ax+b(a、b为常数,a≠0)(1)
a称为斜率,b称为截距。
当两个变量x、y满足式(1)的关系时,称变量y和变量x是一次函数关系。
一次函数的图像如下图的直线所示。

例1一次函数y=2x+1的图像如图所示,截距为1,斜率为2。

以上是一个自变量的情形。这个一次函数关系也同样适用于多个自变量的情形。例如,有两个变量x1、x2,当它们满足下式的关系时,称y和x1、x2是一次函数关系。
y=ax1+bx2+c(a、b、c为常数,a≠0,b≠0)
我们将会在后面讲到,在神经网络中,神经单元的加权输入可以表示为一次函数关系。例如,神经单元有三个来自下层的输入,其加权输入z的式子如下所示(1-3节)。
![]()
如果把作为参数的权重w1、w2、w3与偏置b看作常数,那么加权输入z和x1、x2、x3是一次函数关系。另外,在神经单元的输入x1、x2、x3作为数据值确定了的情况下,加权输入z和权重w1、w2、w3以及偏置b是一次函数关系。用误差反向传播法推导计算式时,这些一次函数关系使得计算可以简单地进行。
问题1作出一次函数y=-2x-1的图像。
| 解如右图所示,截距是-1,斜率是-2。 |  |
二次函数
在数学函数中,二次函数与一次函数同样重要。本书中的代价函数使用了二次函数。二次函数由下式表示。
![]()
二次函数的图像是把物体抛出去时物体所经过的轨迹,也就是抛物线(下图)。这个图像中重要的一点是,a为正数时图像向下凸,从而存在最小值。这个性质是后面讲到的最小二乘法的基础。

例2二次函数![]() 的图像如下图所示。从图像中可以看到,当x=1时,函数取得最小值2。
的图像如下图所示。从图像中可以看到,当x=1时,函数取得最小值2。

以上考察了一个自变量的情形。这里考察的性质在推广到多个自变量的情形时也是不变的。例如,有两个自变量x1、x2时,称下面的函数为关于x1、x2的二次函数。
![]()
这里,a、b、c、p、q、r为常数,a≠0,c≠0。
对于有两个以上的自变量的情形,就难以在纸面上画出图像了。例如,只能像右图那样画出式(3)的图像。

实际的神经网络需要处理更多变量的二次函数。不过,记住这里考察的二次函数的图像后,在理解多变量的情形时应该不难。
注:式(3)所示的图像并不仅限于上图所示的抛物面。
问题2试作出二次函数![]() 的图像。
的图像。
解图像如下图所示

单位阶跃函数
神经网络的原型模型是用单位阶跃函数作为激活函数的(1-2节),它的图像如下所示。

我们用式子来表示单位阶跃函数。

从这个式子我们可以知道,单位阶跃函数在原点处不连续,也就是在原点不可导。由于这个不可导的性质,单位阶跃函数不能成为主要的激活函数。
| 问题3在单位阶跃函数u(x)中,求下面的值。 ①u(-1) ②u(1) ③u(0) 解答案依次为0、1、1。 |
指数函数与Sigmoid函数
具有以下形状的函数称为指数函数。
y=ax(a为正的常数,a≠1)
常数a称为指数函数的底数。纳皮尔数e是一个特别重要的底数,其近似值如下。
e=2.71828...
这个指数函数包含在以下的Sigmoid函数σ(x)的分母中。Sigmoid函数是神经网络中具有代表性的激活函数(1-3节)。
![]()
注:exp是exponential function(指数函数)的简略记法,exp(x)表示指数函数ex。
这个函数的图像如右图所示。可以看出,这个函数是光滑的,也就是处处可导。函数的取值在0和1之间,因此函数值可以用概率来解释。

Sigmoid函数的图像
| 问题4在Sigmoid函数σ(x)中,求以下函数值的近似值。 ①σ(-1) ②σ(0) ③σ(1) 解取e=2.7作为近似值,答案依次为0.27、0.5、0.73。 |
正态分布的概率密度函数
用计算机实际确定神经网络时,必须设定权重和偏置的初始值。求初始值时,正态分布(normaldistribution)是一个有用的工具。使用服从这个分布的随机数,容易取得好的结果。
正态分布是服从以下概率密度函数f(x)的概率分布。

其中常数µ称为期望值(平均值),σ称为标准差。它的图像如下图所示,由于形状像教堂的钟,所以称为钟形曲线。

| 问题5试作出期望值µ为0、标准差σ为1的正态分布的概率密度函数的图像。 解如下图所示,这个正态分布称为标准正态分布。 | |
|
| µ=0,σ=1的正态分布概率密度函数的图像。 |
按照正态分布产生的随机数称为正态分布随机数。在神经网络的计算中,经常用到正态分布随机数作为初始值。
2-2有助于理解神经网络的数列和递推关系式
熟悉了数列和递推关系式之后,就很容易理解误差反向传播法(第4章、第5章)的内容了。因此,下面我们通过简单的例子来回顾一下。
熟悉递推关系式,对于用计算机进行实际计算有很大的帮助。这是因为计算机不擅长导数计算,但擅长处理递推关系式。
数列的含义
数列是数的序列。以下是被称为偶数列的数列。
例12,4,6,8,10,…
数列中的每一个数称为项。排在第一位的项称为首项,排在第二位的项称为第2项,排在第3位的项称为第3项,以此类推,排在第n位的项称为第n项。在上面的例1中,首项为2,第2项为4。
在神经网络的世界中出现的数列是有限项的数列。这样的数列称为有穷数列。在有穷数列中,数列的最后一项称为末项。
例2考察以下有穷数列的例子:
1,3,5,7,9这个数列的首项为1,末项为9,项数为5。
数列的通项公式
数列中排在第n位的数通常用an表示,这里a是数列的名字(数列名a是随意取的,通常用一个拉丁字母或希腊字母来表示)。当想要表示整个数列时,我们使用集合的符号{an}来表示。
将数列的第n项用一个关于n的式子表示出来,这个式子就称为该数列的通项公式。例如,例1的数列的第n项能够用如下关于n的式子写出来,这就是它的通项公式。
![]()
问题1试求以下数列{bn}的通项公式。
1,3,5,7,9,11,…
解通项公式![]() 。
。
在神经网络中,神经单元的加权输入及其输出可以看成数列(1-3节),因为可以像“第几层的第几个神经单元的数值是多少”这样按顺序来确定值。因此,我们用类似数列的符号来表示值,如下例所示。
例3![]() 表示第l层的第j个神经单元的输出值。
表示第l层的第j个神经单元的输出值。
数列与递推关系式
通项公式就是表示数列的项的式子。除此之外数列还存在另一种重要的表示法,就是用相邻项的关系式来表示,这种表示法称为数列的递归定义。
一般地,如果已知首项a1以及相邻两项an、an+1的关系式,就可以确定这个数列,这个关系式称为递推关系式。
例4已知首项a1=1以及关系式an+1=an+2,可以确定以下数列,这个关系式就是数列的递推关系式。
a1=1,a2=a1+1=a1+2=1+2=3,a3=a2+1=a2+2=3+2=5,a4=a3+1=a3+2=5+2=7
递推关系式可以形象地表示为多米诺骨牌。数列由首项以及前后项的关系(也就是递推关系式)确定。此外,图中的数列表示问题1的数列。
例5已知首项C1=3以及递推关系式Cn+1=2Cn,求这个数列{Cn}的前4项。

这样,这个数列就确定了。

数列由首项以及递推关系式cn+1=2cn确定
问题2请递归地定义以下数列{an}。
2,4,6,8,10,…(这是例1的数列)
![]()
联立递推关系式
我们来看看下面的例子。
例6求由以下两个递推关系式定义的数列的前3项,其中a1=b1=1。

可以像下面这样依次计算数列的值an、bn。

像这样,将多个数列的递推关系式联合起来组成一组,称为联立递推关系式。在神经网络的世界中,所有神经单元的输入和输出在数学上都可以认为是用联立递推式联系起来的。例如,我们来看看1-4节的例题中考察过的神经网络的一部分,如下图所示。

我们在第1章考察过的神经网络示例的一部分。此外,有关变量名的内容将在3-1节详述。在箭头前端标记的是权重,神经单元的圆圈中标记的是神经单元的输出变量。于是,如果以a(z)为激活函数,b1(3)、b2(3)为第3层各个神经单元的偏置,根据1-3节,以下关系式成立。

根据这些关系式,第3层的输出a1(3)和a2(3)由第2层的输出a1(2)、a2(2)、a3(2)决定。也就是说,第2层的输出与第3层的输出由联立递推关系式联系起来。第4章和第5章将要考察的误差反向传播法就是将这种递推关系式的观点应用在神经网络中。

2-3神经网络中经常用到的∑符号
Σ是一个需要下功夫来熟悉的符号。如果不理解Σ,在阅读神经网络相关的文献时就比较麻烦。这是因为将加权输入用Σ符号来表示会简洁得多。下面我们就来复习一下这个Σ符号。
注:本书不使用∑符号来进行讲解,因为∑符号使人难以看到数学式的本质。因此,本书中的写法会变得冗长,不便之处还请读者见谅。
∑符号的含义
Σ符号可以简洁地表示数列的总和。除了表示总和以外,并没有别的含义,然而这样过于简洁的表示经常使神经网络的初学者感到苦恼。
注:∑为希腊字母,读作Sigma,对应拉丁字母S,即Sum(总和)的首字母。
对于数列{an},Σ符号的定义式如下所示。

以上用Σ符号表示的和之中,字母k并不具有实质的含义。实际上,在上式的右边没有出现字母k,k在这里仅用于表明关于它求和。因此,这个字母并非必须是k,在数学上通常用i、j、k、l、m、n。

∑符号的性质
Σ符号具有线性性质。这是与微积分共通的性质,可以在式子变形中使用。

证明根据Σ符号的定义,有

下面我们通过例子来验证式(Ⅱ)。


2-4有助于理解神经网络的向量基础
向量的定义为具有大小和方向的量。这里我们主要关注神经网络中用到的内容,弄清向量的性质。
有向线段与向量
有两个点A、B,我们考虑从A指向B的线段,这条具有方向的线段AB叫作有向线段。我们称A为起点,B为终点。

有向线段AB具有以下属性:起点A的位置、指向B的方向,以及AB的长度,也就是大小。在这3个属性中,把方向与大小抽象出来,这样的量叫作向量,通常用箭头表示,总结如下:
向量是具有方向与大小的量,用箭头表示。
有向线段AB所代表的向量用AB表示,也可以用带箭头的单个字母
a或者不带箭头的黑斜体字母a表示。本书主要使用最后一种表示方法。

表示向量的几种方法
向量的坐标表示
把向量的箭头放在坐标平面上,就可以用坐标的形式表示向量。把箭头的起点放在原点,用箭头终点的坐标表示向量,这叫作向量的坐标表示。用坐标表示的向量a如下所示(平面的情况)。
![]()

例1a=(3,2)表示的向量。

例2b=(-2,-1)表示的向量。

例3在三维空间的情况下也是同样的例如,a=(1,2,2)表示右图所示的向量。

向量的大小
从直观上来讲,表示向量的箭头的长度称为这个向量的大小。向量a的大小用|a|表示。
注:符号||是由数的绝对值符号一般化而来的。实际上,数可以看成一维向量。

例4根据右图,如下求得a=(3,4)的大小|a|。

![]()
例5在三维空间的情况下也是同样的例如,如下求得右图所示的向量a=(1,2,2)的大小|a|。

![]()
注:例4、例5都使用了勾股定理。

向量的内积
我们在考虑具有方向的向量的乘积时,包含了“方向与方向的乘积”这样不明确的概念。因此,我们需要一个新的定义——内积。两个向量a、b的内积a·b的定义如下所示。

注:当a、b有一个为0或两者都为0时,内积定义为0。
例6考虑边长为1的正方形ABCD,AB=a,AD=b,AC=c,于是有

|a|=|b|=1,|c|=2
此外,a与a的夹角为0°,a与b的夹角为90°,a与c的夹角为45°,因此有

问题2在上述例6中,求bc。

在三维空间的情况下也是同样的。
例7在边长为3的立方体ABCD-EFGH中,有
 |  |

柯西-施瓦茨不等式
根据内积的定义式(2),我们可以推导出下式,该式在应用上十分重要。

证明根据余弦函数的性质,对任意的θ,有-1≤cosθ≤1,两边同时乘以|a||b|,有
-|a||b|≤|a||b|cosθ≤|a||b|
利用定义式(2),我们可以得到式(3)。
让我们通过图形来考察式(3)。两个向量a、b的大小固定时,有下图(1)、(2)、(3)的3种关系。

根据柯西-施瓦茨不等式(3),可以得出以下事实。
①当两个向量方向相反时,内积取得最小值。
②当两个向量不平行时,内积取平行时的中间值。
③当两个向量方向相同时,内积取得最大值。
性质①就是后述的梯度下降法(2-10节以及第4章、第5章)的基本原理。
另外,可以认为内积表示两个向量在多大程度上指向相同方向。如果将方向相似判定为“相似”,则两个向量相似时内积变大。后面我们考察卷积神经网络时,这个观点就变得十分重要(附录C)。

通过内积可以知道两个向量的相对的相似度。
内积的坐标表示
下面我们使用坐标表示的方式来表示定义式(2)。在平面的情况下,下式成立。

例8当a=(2,3),b=(5,1)时,a.b=2.5+3.1=13,a.a=2.2+3.3=13,b.b=5.5+1.1=26
在三维空间的情况下,内积的坐标表示如下所示,只是在平面情况下的式(4)中添加了z分量。

注:这里我们省略了式(4)、(5)的证明。此外,也有很多文献使用式(4)、(5)作为内积的定义。
例9当a=(2,3,2),b=(5,1,-1)时,a.b=2.5+3.1+2.(-1)=11,a.a=2.2+3.3+2.2=17

向量的一般化
到目前为止,我们考察了平面(也就是二维空间)以及三维空间中的向量。向量的方便之处在于,二维以及三维空间中的性质可以照搬到任意维空间中。神经网络虽然要处理数万维的空间,但是二维以及三维空间的向量性质可以直接利用。出于该原因,向量被充分应用在后述的梯度下降法中(2-10节以及第4章、第5章)。
为了为后面做好准备,我们将目前考察过的二维以及三维空间中的向量公式推广到任意的n维空间。
| ·向量的坐标表示:a=(a1,a2,…,an) ·内积的坐标表示:对于两个向量a=(a1,a2,…,an),b=(b1,b2,…,bn),其内积ab如下式所示。 a·b=a1b1+a2b2+…+anbn ·柯西-施瓦茨不等式:-|a||b|≤a·b≤|a||b| |
例10神经单元有多个输入x1,x2,…,xn时,将它们整理为如下的加权输入。
![]()
其中,w1,w2,…,wn为权重,b为偏置。
使用w=(w1,w2,…,wn),x=(x1,x2,…,xn)这两个向量,我们可以将加权输入表示为内积形式,如下所示。

z=w·x+b
从例10可以看出,在神经网络的世界中,向量的观点是十分有益的。

2-5有助于理解神经网络的矩阵基础
神经网络的文献中会用到矩阵(matrix)。矩阵可以使数学式的表示变简洁。下面我们来梳理一下阅读文献时所需要的矩阵知识。
注:本书从第3章以后的讲解不需要矩阵的知识作为前提。
●什么是矩阵
矩阵是数的阵列,如下所示。

横排称为行,竖排称为列。在上例中,矩阵由3行3列构成,称为3行3列的矩阵。
特别地,如上例所示,行数与列数相同的矩阵称为方阵。此外,如下所示的矩阵X、Y分别称为列向量、行向量,也可以简单地称为向量。

我们将矩阵A推广到更一般的情形,如下所示。

这是m行n列的矩阵。位于第i行第j列的值(称为元素)用aij表示。
有一种有名的矩阵称为单位矩阵,它是对角线上的元素aii为1、其他元素为0的方阵,通常用E表示。例如,2行2列、3行3列的单位矩阵E(称为2阶单位矩阵、3阶单位矩阵)分别如下表示。

注:E为德语中表示1的单词Ein的首字母。
●矩阵相等
两个矩阵A、B相等的含义是它们对应的元素相等,记为A=B。

●矩阵的和、差、常数倍
两个矩阵A、B的和A+B、差A-B定义为相同位置的元素的和、差所产生的矩阵。此外,矩阵的常数倍定义为各个元素的常数倍所产生的矩阵。我们通过以下例子来理解。

●矩阵的乘积
矩阵的乘积在神经网络的应用中特别重要。对于两个矩阵A、B,将A的第i行看作行向量,B的第j列看作列向量,将它们的内积作为第i行第j列元素,由此而产生的矩阵就是矩阵A、B的乘积AB。

请通过下面的例子弄清矩阵乘积的含义。

从这个例子中可以看出,矩阵的乘法不满足交换律。也就是说,除了例外情况,以下关系式成立。
AB≠BA
而单位矩阵E与任意矩阵A的乘积都满足以下交换律。
AE=EA=A
单位矩阵是具有与1相同性质的矩阵。
●Hadamard乘积
对于相同形状的矩阵A、B,将相同位置的元素相乘,由此产生的矩阵称为矩阵A、B的Hadamard乘积,用A⊙B表示。
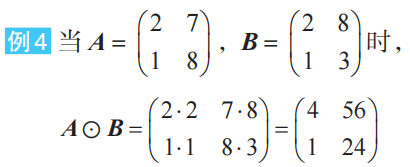
●转置矩阵
将矩阵A的第i行第j列的元素与第j行第i列的元素交换,由此产生的矩阵称为矩阵A的转置矩阵(transposed matrix),用tA、At等表示。下面我们使用tA。

注:阅读神经网络的文献时需要注意,转置矩阵有各种各样的表示方法。

2-6神经网络的导数基础
之前我们提到过,神经网络会自己进行学习,这在数学上的含义是指,对权重和偏置进行最优化(2-12节),使得输出符合学习数据。而对于最优化而言,求导是不可缺少的一种方法。
注:本章所考察的函数都是充分光滑的函数。
导数的定义
函数y=f(x)的导函数f'(x)的定义如下所示。

注:希腊字母Δ读作delta,对应拉丁字母D。此外,带有'(prime)符号的函数或变量表示导函数。
“lim(Δx的式子)”是指当Δx无限接近0时“(Δx的式子)”接近的值。
Δx→0
例1当f(x)=3x时,

例2当f(x)=x2时,

已知函数f(x),求导函数f'(x),称为对函数f(x)求导。当式(1)的值存在时,称函数可导。
导函数的含义如下图所示。作出函数f(x)的图像,f'(x)表示图像切线的斜率。因此,具有光滑图像的函数是可导的。

导函数的含义。f'(x)表示图像切线的斜率。实际上,如果Q无限接近P(也就是∆x→0),那么直线PQ无限接近切线l。
神经网络中用到的函数的导数公式
我们很少使用定义式(1)来求导函数,而是使用导数公式。下面我们就来看一下在神经网络的计算中使用的函数的导数公式(x为变量、c为常数)。

注:这里省略了证明。e为纳皮尔数(2-1节)。
导数符号
在式(1)中,函数y=f(x)的导函数用f'(x)表示,但也存在不同的表示方法,例如可以用如下的分数形式来表示。

这个表示方法是十分方便的,这是因为复杂的函数可以像分数一样计算导数。关于这一点,我们会在后文中说明。

导数的性质
利用下式,可导函数的世界得到了极大的扩展。

注:组合起来也可以简单地表示为{f(x)–g(x)}′=f′(x)–g′(x)。
式(3)称为导数的线性性。用文字来表述可能更容易记忆,如下所示。
和的导数为导数的和,常数倍的导数为导数的常数倍。
导数的线性性是后述的误差反向传播法背后的主角。


分数函数的导数和Sigmoid函数的导数
当函数是分数形式时,求导时可以使用下面的分数函数的求导公式。
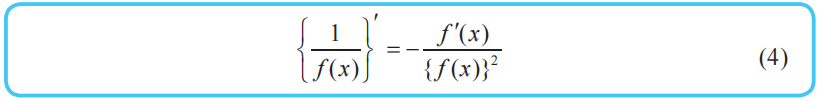
注:这里省略了证明。函数f(x)不取0值。
Sigmoid函数σ(x)是神经网络中最有名的激活函数之一,其定义如下所示(2-1节)。

在后述的梯度下降法中,需要对这个函数求导。求导时使用下式会十分方便。

利用该式,即使不进行求导,也可以由σ(x)的函数值得到Sigmoid函数的导函数的值。


上式可以像下面这样变形。

将σ(x)提取出来,就得到了式(5)。
最小值的条件
由于导函数f'(x)表示切线斜率,我们可以得到以下原理,该原理在后述的最优化(2-12节)中会用到。

导函数f'(a)表示切线斜率,所以根据下图可以清楚地看出f'(a)=0。

应用时请记住以下事实。
注:已知命题p、q,由p可以推出q,则q称为p的必要条件。
从下面的函数y=f(x)的图像可以清楚地看出这一点。

在通过后述的梯度下降法求最小值时,这个性质有时会成为很大的障碍。

解首先我们求出导函数。
![]()
然后,我们可以做出以下表格(称为增减表)。
| x | … | -1 | … | 0 | … | 2 | … |
| f'(x) | - | 0 | + | 0 | - | 0 | + |
| f(x) | ↘ | 27 | ↗ | 32 | ↘ | 0 | ↗ |
(极小) (极大 ) (最小)
注:增大、减小用↗、↘表示,区间用…表示。
从表中可以看出,f(x)在点x=2处取得最小值0。
如果已知增减表,就可以画出函数图像的大体形状。这里我们使用例题中的增减表,画出函数
的图像,如右图所示。
|
|

2-7神经网络的偏导数基础
神经网络的计算往往会涉及成千上万个变量,这是因为构成神经网络的神经单元的权重和偏置都被作为变量处理。下面我们就来考察一下神经网络的计算中所需的多变量函数的导数。
注:本节所考察的函数是充分光滑的函数。
多变量函数
例1![]()
多变量函数难以直观化。例如,即使是像例1那样简单的函数,其图像也是非常复杂的,如下图所示。

描述神经网络的函数的变量有成千上万个,因此难以从直观上理解这些函数。不过,只要理解了单变量的情况,我们就可以将多变量的情况作为其扩展来理解,这样就不会那么困难了。
单变量函数用f(x)表示,仿照单变量函数,多变量函数可以如下表示。
例2f(x,y):有两个自变量x、y的函数。
例3f(x1,x2,…,xn):有n个自变量x1,x2,…,xn的函数。
偏导数
求导的方法也同样适用于多变量函数的情况。但是,由于有多个变量,所以必须指明对哪一个变量进行求导。在这个意义上,关于某个特定变量的导数就称为偏导数(partial derivative)。
例如,让我们来考虑有两个变量x、y的函数z=f(x,y)。只看变量x,将y看作常数来求导,以此求得的导数称为“关于x的偏导数”,用下面的符号来表示。

关于y的偏导数也是同样的。

下面,我们通过例4和问题1、问题2来看一下神经网络中用到的偏导数的代表性例子。



多变量函数的最小值条件
光滑的单变量函数y=f(x)在点x处取得最小值的必要条件是导函数在该点取值0(2-6节),这个事实对于多变量函数同样适用。例如对于有两个变量的函数,可以如下表示。

上述(1)很容易扩展到一般的具有n个变量的情形。
此外,从下图可以清楚地看出上述(1)是成立的。因为从x方向以及y方向来看,函数z=f(x,y)取得最小值的点就像葡萄酒杯的底部。

就像我们之前所确认的那样(2-6节),上述(1)所示的条件是必要条件。即使满足上述(1),也不能保证函数f(x,y)在该点处取得最小值。
例5求函数z=x2+y2取得最小值时x、y的值。首先,我们来求关于x、y的偏导数。

根据上述(1),函数取得最小值的必要条件是x=0,y=0。此时函数值z为0。由于z=x2+y2≥0,所以我们知道这个函数值0就是最小值。通过前面的例1的函数图像,我们也可以确认这个事实。

2-8误差反向传播法必需的链式法则
下面我们来考察有助于复杂函数求导的链式法则。这个法则对于理解后述的误差反向传播法很有必要。
注:本节考察的函数是充分光滑的函数。
神经网络和复合函数
已知函数y=f(u),当u表示为u=g(x)时,y作为x的函数可以表示为形如y=f(g(x))的嵌套结构(u和x表示多变量)。这时,嵌套结构的函数f(g(x))称为f(u)和g(x)的复合函数。
例1函数z=(2-y)2是函数u=2-y和函数z=u2的复合函数。

例2对于多个输入x1,x2,…,xn,将a(x)作为激活函数,求神经单元的输出y的过程如下所示(1-3节)。
![]()
w1,w2,…,wn为各输入对应的权重,b为神经单元的偏置。这个输出函数是如下的x1,x2,…,xn的一次函数f和激活函数a的复合函数。

 单变量函数的链式法则
单变量函数的链式法则
已知单变量函数y=f(u),当u表示为单变量函数u=g(x)时,复合函数f(g(x))的导函数可以如下简单地求出来。
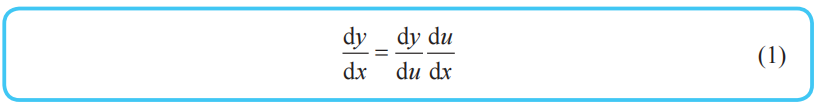
这个公式称为单变量函数的复合函数求导公式,也称为链式法则。本书使用“链式法则”这个名称。

观察式(1)的右边,如果将dx、dy、du都看作一个单独的字母,那么式(1)的左边可以看作将右边进行简单的约分的结果,这个看法总是成立的。通过将导数用dx、dy等表示,我们可以这样记忆链式法则:“复合函数的导数可以像分数一样使用约分。”
注:这个约分的法则不适用于dx、dy的平方等情形。
例3当y为u的函数,u为v的函数,v为x的函数时,


多变量函数的链式法则
在多变量函数的情况下,链式法则的思想也同样适用。只要像处理分数一样对导数的式子进行变形即可。然而事情并没有这么简单,因为必须对相关的全部变量应用链式法则。
我们来考察两个变量的情形。
变量z为u、v的函数,如果u、v分别为x、y的函数,则z为x、y的函数,此时下式(多变量函数的链式法则)成立。


变量z为u、v的函数,u、v分别为x、y的函数,z关于x求导时,先对u、v求导,然后与z的相应导数相乘,最后将乘积加起来。
例4与上面式(2)一样,下式也成立。
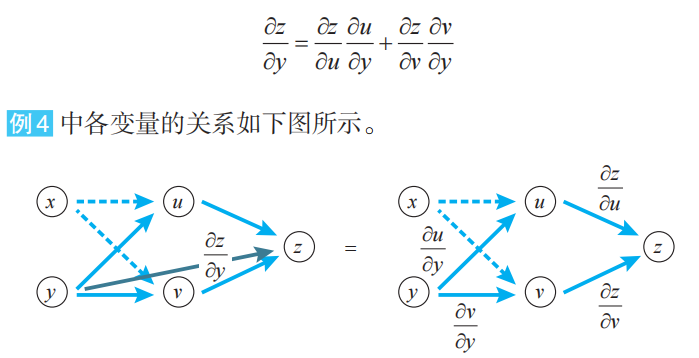

上式在三个以上的变量的情况下也同样成立。

2-9梯度下降法的基础:多变量函数的近似公式
梯度下降法是确定神经网络的一种代表性的方法。在应用梯度下降法时,需要用到多变量函数的近似公式。
注:本节所考察的函数是充分光滑的函数。
单变量函数的近似公式
首先我们来考察单变量函数y=f(x)。如果x作微小的变化,那么函数值y将会怎样变化呢?答案就在导函数的定义式中(2-6节)。

在这个定义式中,∆x为“无限小的值”,不过若将它替换为“微小的值”,也不会造成很大的误差。因而,下式近似成立。

将上式变形,可以得到以下单变量函数的近似公式。


这就是例1的解答。
下面的图像是将y=ex与y=1+x画在一张图上。在x=0附近两个函数的图像重叠在一起,由此可以确认例1的解答是正确的。

多变量函数的近似公式
下面我们将单变量函数的近似公式(1)扩展到两个变量的函数。如果x、y作微小的变化,那么函数z=f(x,y)的值将会怎样变化呢?答案是以下的近似公式。Δx、Δy为微小的数。


上式表示当x、y依次变化Δx、Δy时函数z=f(x,y)的变化,于是式(2)可以像下面这样简洁地表示。

通过这样的表示方式,就很容易将近似公式(2)进行推广。例如,变量z为三个变量w、x、y的函数时,近似公式如下所示。
近似公式的向量表示
三个变量的函数的近似公式(4)可以表示为如下两个向量的内积▽z.Δx的形式。

注:▽通常读作nabla(2-10节)。
我们可以很容易地想象,对于一般的n变量函数,近似公式也可以像这样表示为内积的形式。这个事实与下一节要考察的梯度下降法的原理有关。

2-10梯度下降法的含义与公式
应用数学最重要的任务之一就是寻找函数取最小值的点。本节我们来考察一下著名的寻找最小值的点的方法——梯度下降法。在第4章和第5章中我们将会看到,梯度下降法是神经网络的数学武器。
本节主要通过两个变量的函数来展开讨论。在神经网络的计算中,往往需要处理成千上万个变量,但其数学原理和两个变量的情形是相同的。
注:同样,本节考察的函数是充分光滑的函数。
梯度下降法的思路
已知函数z=f(x,y),怎样求使函数取得最小值的x、y呢?最有名的方法就是利用“使函数z=f(x,y)取得最小值的x、y满足以下关系”这个事实(2-7节)。

这是因为,在函数取最小值的点处,就像葡萄酒杯的底部那样,与函数相切的平面变得水平。

然而,在实际问题中,联立方程式(1)通常不容易求解,那么该如何解决呢?梯度下降法是一种具有代表性的替代方法。该方法不直接求解式(1)的方程,而是通过慢慢地移动图像上的点进行摸索,从而找出函数的最小值。
我们先来看看梯度下降法的思路。这里我们将图像看作斜坡,在斜坡上的点P处放一个乒乓球,然后轻轻地松开手,球会沿着最陡的坡面开始滚动,待球稍微前进一点后,把球止住,然后从止住的位置再次松手,乒乓球会从这个点再次沿着最陡的坡面开始滚动。

这个操作反复进行若干次后,乒乓球沿着最短的路径到达了图像的底部,也就是函数的最小值点。梯度下降法就模拟了这个球的移动过程。

在数值分析领域,梯度下降法也称为最速下降法。这个名称表示沿着图像上的最短路径下降。
近似公式和内积的关系
让我们依照前面考察过的思路来将梯度下降法正式化。
函数z=f(x,y)中,当x改变Δx,y改变Δy时,我们来考察函数f(x,y)的值的变化Δz。
Δz=f(x+Δx,y+Δy)-f(x,y)根据近似公式(2-9节),以下关系式成立。


我们在上一节也提到过,式(2)的右边可以表示为如下两个向量的内积(2-4节)形式。

请大家注意这个内积的关系,这就是梯度下降法的出发点。

式(2)左边的∆z可以用式(3)的两个向量的内积形式来表示。
向量内积的回顾
我们来考察两个固定大小的非零向量a、b。当b的方向与a相反时,内积a·b取最小值(2-4节)。

换句话说,当向量b满足以下条件式时,可以使得内积a·b取最小值。
b=-ka(k为正的常数)(4)
内积的这个性质(4)就是梯度下降法的数学基础。
二变量函数的梯度下降法的基本式
当x改变∆x,y改变∆y时,函数f(x,y)的变化∆z为式(2),可以表示为式(3)的两个向量的内积。根据式(4),当两个向量方向相反时,内积取最小值。也就是说,当式(3)的两个向量的方向恰好相反时,式(2)的∆z达到最小(即减小得最快)。

(x,y)向点(x+∆x,y+∆y)移动时,当满足以下关系式时,函数z=f(x,y)减小得最快。这个关系式就是二变量函数的梯度下降法的基本式。

注:希腊字母η读作ita,对应拉丁字母i。这里也可以像式(4)那样使用字母k,不过大多数文献中采用η。
利用关系式(5),如果
从点(x,y)向点(x+∆x,y+∆y)移动 (6)
就可以从图像上点(x,y)的位置最快速地下坡。
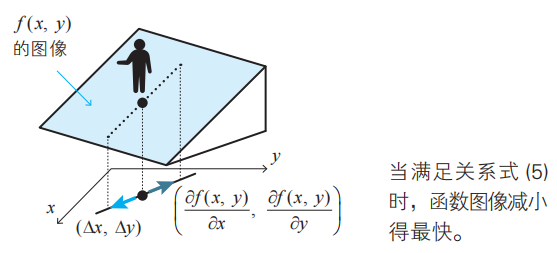
式(5)右边的向量 称为函数f(x,y)在点(x,y)处的梯度(gradient)。这个名称来自于它给出了最陡的坡度方向。
称为函数f(x,y)在点(x,y)处的梯度(gradient)。这个名称来自于它给出了最陡的坡度方向。


梯度下降法及其用法
为了弄清梯度下降法的思路,前面我们考察了乒乓球的移动方式。由于在不同的位置陡坡的方向也各不相同,通过反复进行“一边慢慢地移动位置一边寻找陡坡”的操作,最终可以到达函数图像的底部,也就是函数的最小值点。
下山的情形也是一样的。最陡的下坡方向在每个位置各不相同。因此,要想通过最短路径下山,就必须一边慢慢地下坡一边在每个位置寻找最陡的坡度。
在函数的情况下也完全一样。要寻找函数的最小值,可以利用式(5)找出减小得最快的方向,沿着这个方向依照上述(6)稍微移动。在移动后到达的点处,再次利用式(5)算出方向,再依照上述(6)稍微移动。通过反复进行这样的计算,就可以找到最小值点。这种寻找函数f(x,y)的最小值点的方法称为二变量函数的梯度下降法。

下一节我们将用Excel来体验梯度下降法,以便更具体地理解上面讲解的内容。
将梯度下降法推广到三个变量以上的情况
二变量函数的梯度下降法的基本式(5)可以很容易地推广到三个变量以上的情形。当函数f由n个自变量x1,x2,…,xn构成时,梯度下降法的基本式(5)可以像下面这样进行推广。

这里,以下向量称为函数f在点(x1,x2,…,xn)处的梯度。

与二变量函数的情况一样,利用这个关系式(7),如果
从点(x1,x2,…,xn)向点(x1+Δx1,x2+Δx2,…,xn+Δxn)移动 (8)
就能够沿着函数减小得最快的方向移动。因此,反复依照上述(8)来移动,就能够在n维空间中算出坡度最陡的方向,从而找到最小值点。这就是n变量情况下的梯度下降法。
此外,由于式(7)、(8)是n维的,难以在纸上画出其图像。大家可以利用二变量情况下的式(5)、(6)来直观地理解。
哈密顿算子▽
在实际的神经网络中,主要处理由成千上万个变量构成的函数的最小值。在这种情况下,像式(7)那样的表示往往就显得十分冗长。因此我们来考虑更简洁的表示方法。
在数学的世界中,有一个被称为向量分析的领域,其中有一个经常用到的符号▽。▽称为哈密顿算子,其定义如下所示。

利用这个符号,式(7)可以如下表示。

例1对于二变量函数f(x,y),梯度下降法的基本式(5)如下所示。
(Δx,Δy)=-η▽f(x,y)
例2对于三变量函数f(x,y,z),梯度下降法的基本式(7)如下所示。
(Δx,Δy,Δz)=-η▽f(x,y,z)
其中,左边的向量(Δx1,Δx2,…,Δxn)称为位移向量,记为Δx。Δx=(Δx1,Δx2,…,Δxn)利用这个位移向量,梯度下降法的基本式(7)可以更简洁地表示。

η的含义以及梯度下降法的要点
到目前为止,η只是简单地表示正的微小常数。而在实际使用计算机进行计算时,如何恰当地确定这个η是一个大问题。
从式(5)的推导过程可知,η可以看作人移动时的“步长”,根据η的值,可以确定下一步移动到哪个点。如果步长较大,那么可能会到达最小值点,也可能会直接跨过了最小值点(左图)。而如果步长较小,则可能会滞留在极小值点(右图)。

在神经网络的世界中,η称为学习率。遗憾的是,它的确定方法没有明确的标准,只能通过反复试验来寻找恰当的值。
2-11用Excel体验梯度下降法
梯度下降法是神经网络计算的基础,下面我们就通过Excel来弄清它的含义。在观察逻辑过程时,Excel是一个优秀的工具,通过工作表我们可以直观地看出梯度下降法是什么样的。例如,我们用Excel来求解以下问题。
例题对于函数z=x2+y2,请用梯度下降法求出使函数取得最小值的x、y值。
注:我们在2-7节的例5中考察过,正确答案为(x,y)=(0,0)。另外,2-节中画了这个函数的图像,大家可以参考一下。
解首先求出梯度。

接下来,我们逐步进行计算。
①初始设定
随便给出初始位置(xi,yi)(i=0)与学习率η。

②计算位移向量
对于当前位置(xi,yi),算出梯度式(1),然后根据梯度下降法的基本式(2-10节式(5)),求位移向量Δx=(△xi,Δyi)。根据式(1),可得

③更新位置
根据梯度下降法,由下式求出从当前位置(xi,yi)移动到的点(xi+1,yi+1)。


④反复执行②~③的操作
下图是反复执行②~③的操作30次后得出的坐标(x30,y30)的值。这与2-7节的例5的正解(x,y)=(0,0)一致。


2-12最优化问题和回归分析
在为了分析数据而建立数学模型时,通常模型是由参数确定的。在数学世界中,最优化问题就是如何确定这些参数。
从数学上来说,确定神经网络的参数是一个最优化问题,具体就是对神经网络的参数(即权重和偏置)进行拟合,使得神经网络的输出与实际数据相吻合。
为了理解最优化问题,最浅显的例子就是回归分析。下面我们就利用简单的回归分析问题来考察最优化问题的结构。
什么是回归分析
由多个变量组成的数据中,着眼于其中一个特定的变量,用其余的变量来解释这个特定的变量,这样的方法称为回归分析。回归分析的种类有很多。为了理解它的思想,我们来考察一下最简单的一元线性回归分析。
一元线性回归分析是以两个变量组成的数据为考察对象的。下图给出了两个变量x、y的数据以及它们的散点图。
一元线性回归分析是用一条直线近似地表示右图所示的散点图上的点列,通过该直线的方程来考察两个变量之间的关系。这条近似地表示点列的直线称为回归直线。

这条回归直线用一次关系式表示如下:
y=px+q(p、q为常数) (1)
这个式子称为回归方程。
x、y是为了将构成数据的各个值代入而设定的变量,右边的x称为自变量,左边的y称为因变量。常数p、q是这个回归分析模型的参数,由给出的数据来决定。
注:p称为回归系数,q称为截距。
通过具体例子来理解回归分析的逻辑
下面让我们通过具体的例子来看看回归方程(1)是如何确定的。

解设所求的回归方程如下所示。
y=px+q(p、q为常数)(2)
将第k个学生的身高记为xk,体重记为yk,可以求得第k个学生的回归分析预测的值(称为预测值),如下所示。
pxk+q(3)
我们将这些预测值加以汇总,如下表所示。
| 编号 | 身高x | 体重y | 预测值px+q |
| 1 | 153.3 | 45.5 | 153.3p+q |
| 2 | 164.9 | 56.0 | 164.9p+q |
| 3 | 168.1 | 55.0 | 168.1p+q |
| 4 | 151.5 | 52.8 | 151.5p+q |
| 5 | 157.8 | 55.6 | 157.8p+q |
| 6 | 156.7 | 50.8 | 156.7p+q |
| 7 | 161.1 | 56.4 | 161.1p+q |
y的实测值和预测值。在考虑数学上的最优化问题时,理解实测值和预测值的差异是十分重要的
如下算出实际的体重yk与预测值的误差ek。

这些ek的值既可以为正也可以为负。接下来我们来考虑下面的值Ck,这个值称为平方误差。

注:系数1/2是为了方便进行之后的处理,这个值对结论没有影响。
遍历全体数据,将它们的平方误差加起来,假设得到的值为CT。CT=C1+C2+…+C7
根据之前的表以及式(5),用p、q的式子表示误差总和CT,如下所示。

我们的目标是确定常数p、q的值。回归分析认为,p、q是使误差总和式(6)最小的解。知道这个解的思路后,后面就简单了。我们利用以下的最小值条件即可(2-7节)

我们来实际计算一下式(6)。根据偏导数的链式法则(2-8节),可得

整理后得到下式。
1113.4p+7q=372.1,177312p+1113.4q=59274
解这个联立方程,可得p=0.41,q=-12.06从而求得目标回归方程(2),如下所示。
y=0.41x–12.06
注:这时CT=27.86。

以上就是一元线性回归分析中使用的回归直线的确定方法。这里的重点是最优化问题的求解思路。这里所考察的最优化方法在后面的神经网络的计算中也可以直接使用。
代价函数
在最优化方面,误差总和CT可以称为“误差函数”“损失函数”“代价函数”等。本书采用代价函数(cost function)这个名称。
注:之所以不使用误差函数(error function)、损失函数(lost function)的叫法,是因为它们的首字母容易与神经网络中用到的熵(entropy)、层(layer)的首字母混淆。
此外,除了这里所考察的平方误差的总和CT之外,根据不同的思路,代价函数还存在其他多种形式。利用平方误差的总和CT进行最优化的方法称为最小二乘法。本书中我们只考虑将平方误差的总和CT作为代价函数。
模型参数的个数
我们再来看看之前的例题。模型有2个参数p、q,而已知的条件(数据的规模)有7个。也就是说,模型的参数的个数(2个)小于条件的个数(7个)。反过来说,回归方程是根据大量的条件所得到的折中结果。这里所说的“折中”是指,理想中应该取值0的代价函数式(6)只能取最小值。因此,模型与数据的误差CT不为0也无须担心。不过,只要误差接近0,就可以说这是合乎数据的模型。
此外,模型的参数个数大于数据规模时又如何呢?当然,这时参数就不确定了。因此,要确定模型,就必须准备好规模大于参数个数的数据。





