vae笔记

油管博主推荐 Deepia｜ 一个动画视频讲明白VAE_哔哩哔哩_bilibili 

在概率论与机器学习中，表达式 p(x∣z)p(x∣z) 和 p(z∣x)p(z∣x) 是两个非常重要的条件概率，它们分别表示：
🔹 1. p(x∣z)p(x∣z)：给定 z 的情况下 x 的分布含义：已知隐变量或类别 z，观测到数据 x 的概率。又称为似然函数（Likelihood）。常用于：生成模型中，比如 VAE（变分自编码器）、GMM（高斯混合模型）等。如果 z 表示类别标签，p(x|z) 就是该类别的数据分布。✅ 举例：假设你有一个猫和狗的图像分类任务：z=0z=0 表示“猫”，z=1z=1 表示“狗”， 那么 p(x∣z=0)p(x∣z=0) 就是“给定这是一个猫的照片，出现图像 x 的概率”。🔹 2. p(z∣x)p(z∣x)：给定 x 的情况下 z 的分布含义：已知观测数据 x，推测其对应的隐变量或类别 z 的概率。又称为后验概率（Posterior）。常用于：分类问题中：给定输入图像 x，预测它是猫还是狗的概率。推断问题中：从观测数据中推断出潜在结构或类别。✅ 举例：继续上面的例子：给你一张图片 x，想知道它更可能是猫（z=0）还是狗（z=1），那么你要计算的就是 p(z=0∣x)p(z=0∣x) 和 p(z=1∣x)p(z=1∣x)。🔄 它们之间的关系：贝叶斯公式这两个条件概率之间可以通过贝叶斯定理相互转换：
p(z∣x)=p(x∣z)p(z)p(x)
p(z∣x)=p(x)p(x∣z)p(z)​其中：p(x∣z)p(x∣z)：似然（Likelihood）p(z)p(z)：先验（Prior）p(x)p(x)：证据（Evidence，常数）

在概率论与机器学习中，符号 p(x)p(x) 和 p(z)p(z) 是非常常见也非常基础的概率分布表达式。它们分别表示：
🟢 1. p(x)p(x)：数据的边缘分布（Marginal Distribution of x）
✅ 含义：p(x)p(x) 表示的是观测变量 xx 的整体分布情况。它不依赖于任何其他变量，是“无条件”的。可以理解为：在没有其他信息的情况下，某个观测值 xx 出现的概率。🧠 直观理解：比如你在做图像识别任务，xx 是一张图片，那么 p(x)p(x) 就描述了所有可能的图像在整个图像空间中的出现频率或密度。
🔍 数学上如何计算它？如果存在一个隐变量 zz，根据全概率公式有：
p(x)=∑zp(x∣z)p(z)（离散情况）
p(x)=z∑​p(x∣z)p(z)（离散情况）或者：
p(x)=∫p(x∣z)p(z)dz（连续情况）
p(x)=∫p(x∣z)p(z)dz（连续情况）
🟢 2. p(z)p(z)：隐变量的先验分布（Prior Distribution of z）
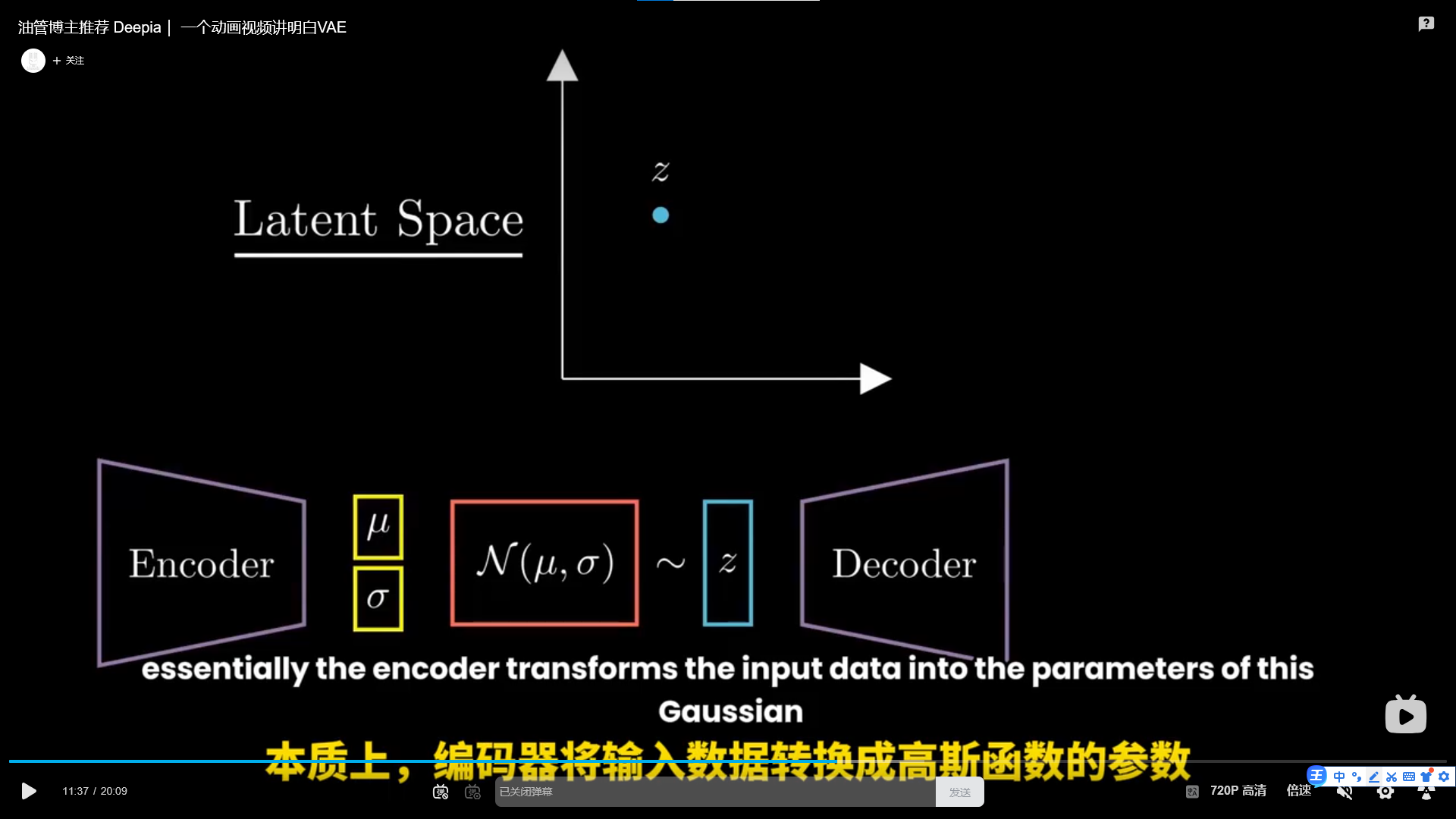
✅ 含义：p(z)p(z) 表示的是隐变量 zz 的先验分布。在没有看到任何观测数据 xx 的情况下，我们对 zz 的信念或假设。常用于生成模型、贝叶斯推断等场景。🧠 直观理解：比如在 VAE（变分自编码器）中，zz 是图像的潜在表示（latent code），通常我们假设 zz 服从一个简单的分布，如标准正态分布：
p(z)=N(0,I)
p(z)=N(0,I)这样我们可以从这个分布中采样出不同的 zz，再通过解码器生成不同的 xx。
🔄 总结对比表：
符号	名称	含义说明
p(x)p(x)	数据的边缘分布	所有观测数据的整体分布，可以由 $ p(x
p(z)p(z)	隐变量的先验分布	在没有看到数据之前，对隐变量 zz 的假设（通常是简单分布，如高斯分布）
📌 联系图（生成模型视角）：深色版本p(z) → p(x|z) → p(x)先采样一个隐变量 z∼p(z)z∼p(z)然后根据 zz 生成观测数据 x∼p(x∣z)x∼p(x∣z)所有的 xx 构成了最终的数据分布 p(x)p(x)