用可视化学习双指针法
1.移除元素


int removeElement(int* nums, int numsSize, int val) {int dst = 0; // 慢指针,用于收集非目标值元素// 遍历整个数组for (int src = 0; src < numsSize; src++) {// 如果当前元素不等于要删除的值if (nums[src] != val) {// 保留该元素(复制到dst位置)并移动dstnums[dst] = nums[src];dst++;}// 如果当前元素等于要删除的值,只移动src,不做其他操作}// 返回新数组的长度,即dst的值return dst;
}
我们用可视化的方法来看这道题:
目标:把 [😈, 😊, 😊, 😈] 中所有 😈 移除,留下 [😊, 😊],返回新长度 2。
初始状态:
数组: [😈, 😊, 😊, 😈] (其中😈代表值3,😊代表值2)dst src第一轮:检查src=0时
检查: nums[src](😈) == val(😈)吗?✅ 是要删除的! 跳过它!src++ 向后移动一位
数组: [😈, 😊, 😊, 😈]dst src
第二轮:检查src=1时
检查: nums[src](😊) == val(😈)吗?❌ 不是! 这是要保留的!dst复制+移动,src继续++
数组: [😊, 😊, 😊, 😈]dst src
第三轮:检查src=2时
检查: nums[src](😊) == val(😈)吗?❌ 不是! 又是要保留的元素!
dst复制+移动,src++数组: [😊, 😊, 😊, 😈]dst src第四轮:检查src=3时
检查: nums[src](😈) == val(😈)吗?✅ 是要删除的! 跳过它!
src++(超出范围)数组: [😊, 😊, 😊, 😈]dst src(出界)
最终结果:
更新后数组: [😊, 😊, 😊, 😈]👆dst=2返回值: dst = 2
用mermaid做出的流程图:
2.删除重复元素

先上完整代码,再来可视化
int removeDuplicates(int* nums, int numsSize) {if (numsSize == 0) return 0;int dst = 0; // 慢指针,指向当前无重复区域的末尾// 从索引1开始遍历数组for (int src = 1; src < numsSize; src++) {// 如果发现一个新元素(与慢指针指向的元素不同)if (nums[src] != nums[dst]) {// 将慢指针前移,并复制这个新元素dst++;nums[dst] = nums[src];}// 如果元素重复,只移动快指针,不做其他操作}// 返回无重复区域的长度 = dst + 1return dst + 1;
}
目标:把 [1, 1, 2, 3, 3, 4] 变成 [1, 2, 3, 4],返回新长度 4。
初始状态:
数组: [1, 1, 2, 3, 3, 4]dst src
第一轮:检查src=1(值1)
比较: nums[dst]=1 VS nums[src]=1🤔 一样! 不需要保留
src++
数组: [1, 1, 2, 3, 3, 4]dst src
第二轮:检查src=2(值2)
比较: nums[dst]=1 VS nums[src]=2😲 不一样! 发现新数字
dst移动+复制新数字
数组: [1, 2, 2, 3, 3, 4]dst src
src++
数组: [1, 2, 2, 3, 3, 4]dst src第三轮:检查src=3(值3)
比较: nums[dst]=2 VS nums[src]=3😲 不一样! 又一个新数字
dst移动+复制新数字
数组: [1, 2, 3, 3, 3, 4]dst src
src++
数组: [1, 2, 3, 3, 3, 4]dst src第四轮:检查src=4(值3)
比较: nums[dst]=3 VS nums[src]=3🤔 一样! 跳过这个重复的
src++
数组: [1, 2, 3, 3, 3, 4]dst src
第四轮:检查src=5(值4)
比较: nums[dst]=3 VS nums[src]=4😲 不一样! 最后一个新数字
dst移动+复制新数字
数组: [1, 2, 3, 4, 3, 4]dst srcsrc++
数组: [1, 2, 3, 4, 3, 4]dstsrc(出界)最终结果:
更新后数组: [1, 2, 3, 4, 3, 4]👆dst=3返回值: dst+1 = 4
mermaid生成的流程图: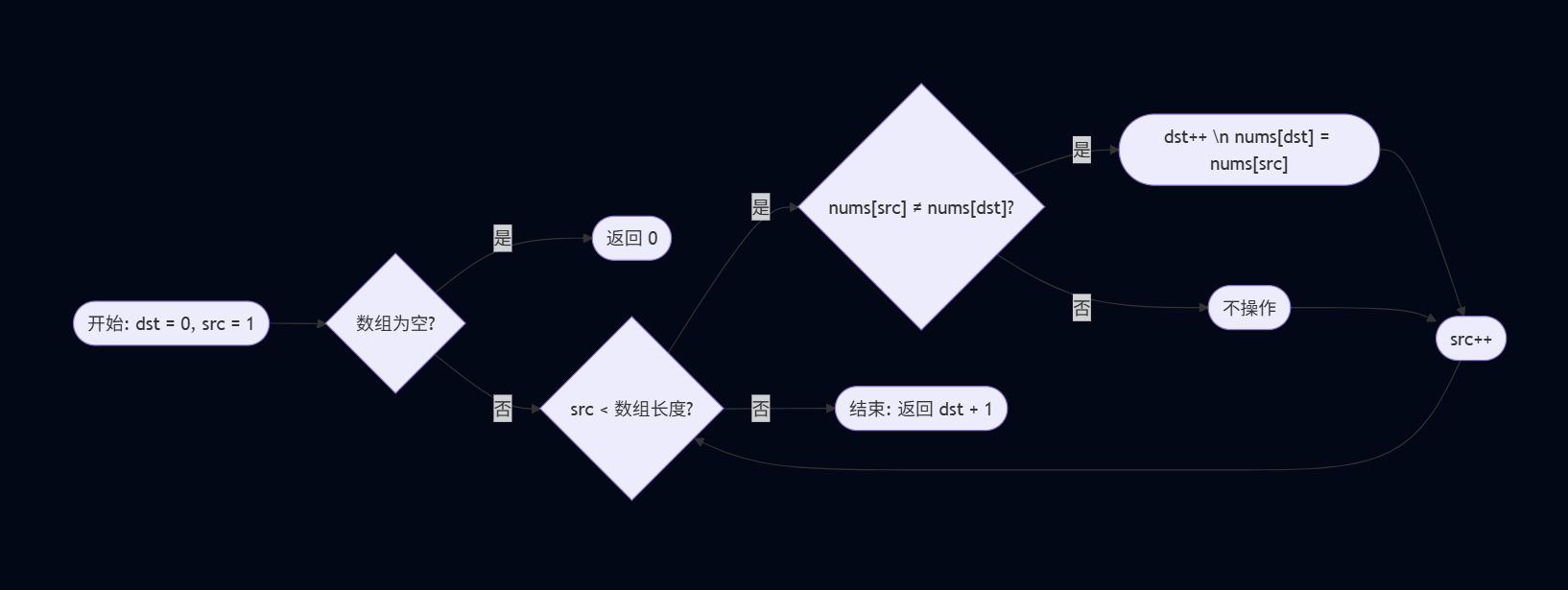
3.合并两个有序数组
依旧是先来代码,再进行可视化
void merge(int* nums1, int m, int* nums2, int n) {int l1 = m - 1; // 指向nums1最后一个有效元素int l2 = n - 1; // 指向nums2最后一个元素int l3 = m + n - 1; // 指向合并后数组的末尾位置// 从后往前合并,每次选取较大的元素放到nums1的末尾while (l1 >= 0 && l2 >= 0) {// 将较大的元素放到l3指向的位置if (nums1[l1] > nums2[l2]) {nums1[l3--] = nums1[l1--];} else {nums1[l3--] = nums2[l2--];}}// 如果nums2还有剩余元素,将它们复制到nums1// 注意: 如果nums1还有剩余元素,它们已经在正确位置上,不需要移动while (l2 >= 0) {nums1[l3--] = nums2[l2--];}
}
目标:将 [1, 2, 3, 0, 0, 0] (nums1) 和 [2, 5, 6] (nums2) 合并成 [1, 2, 2, 3, 5, 6]
初始状态:
nums1: [1, 2, 3, 0, 0, 0]l1 l3
nums2: [2, 5, 6]l2
第一轮:比较l1和l2
谁更大? nums1[l1]=3 VS nums2[l2]=6❌ ✅
nums2元素更大! 6 → 放到l3指向的位置 && l2,l3同时向前移动一位nums1: [1, 2, 3, 0, 0, 6]l1 l3
nums2: [2, 5, 0]l2
第二轮:比较l1和l2
谁更大? nums1[l1]=3 VS nums2[l2]=5❌ ✅
nums2元素更大! 5 → 放到l3指向的位置 && l2,l3同时向前移动一位
nums1: [1, 2, 3, 0, 5, 6]l1 l3
nums2: [2, 0, 0]l2第三轮:比较l1和l2
谁更大? nums1[l1]=3 VS nums2[l2]=2✅ ❌
nums1元素更大! 3 → 放到l3指向的位置 && l1,l3同时向前移动一位
nums1: [1, 2, 3, 3, 5, 6]l1 l3
nums2: [2, 0, 0]l2
第四轮:比较l1和l2
谁更大? nums1[l1]=2 VS nums2[l2]=2🤝 平手! 按规则用nums2的
nums2的2 → 放到l3指向的位置 && l2,l3同时向前移动一位
nums1: [1, 2, 2, 3, 5, 6]l1l3
nums2: [0, 0, 0]l2(出界)
最终检查:l2已经<0,说明nums2元素已全部放入,而nums1剩余元素已经在正确位置,不需要移动。
mermaid生成的流程图:
4.总结
4.1 三种方法对比
| 特性 | 合并有序数组 | 删除重复元素 | 移除元素 |
|---|---|---|---|
| 指针方向 | 从后往前 | 从前往后 | 从前往后 |
| 指针数量 | 3个 | 2个 | 2个 |
| 慢指针功能 | 定位放置位置 | 标记不重复元素边界 | 收集需保留的元素 |
| 快指针功能 | 比较选择元素 | 探索新元素 | 筛选有效元素 |
| 元素处理 | 每次选较大的 | 只保留不重复的 | 只保留非目标值 |
| 返回值 | 无需返回 | dst+1 | dst |
4.2 时间复杂度分析
| 算法 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 合并有序数组 | O(m+n) | O(1) |
| 删除重复元素 | O(n) | O(1) |
| 移除元素 | O(n) | O(1) |
4.3双指针法的核心思想
-
空间效率:所有算法都是原地操作,不需要额外空间
-
指针分工:
-
慢指针:通常负责构建结果或标记边界
-
快指针:负责探索或提供数据
-
-
处理策略:
-
元素保留:满足特定条件时复制并移动慢指针
-
元素丢弃:不满足条件时只移动快指针
-


