当前位置：首页 > news >正文

c++题目_P1027 [NOIP 2001 提高组] Car 的旅行路线

news 来源：原创 2025/5/2 8:13:12

P1027 [NOIP 2001 提高组] Car 的旅行路线 - 洛谷

# P1027 [NOIP 2001 提高组] Car 的旅行路线

## 题目描述

又到暑假了，住在城市 A 的 Car 想和朋友一起去城市旅游。
她知道每个城市都有 $4$ 个飞机场，分别位于一个矩形的 $4$ 个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第 $i$ 个城市中高速铁路的单位里程价格为 $T_i$，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为 $t$。

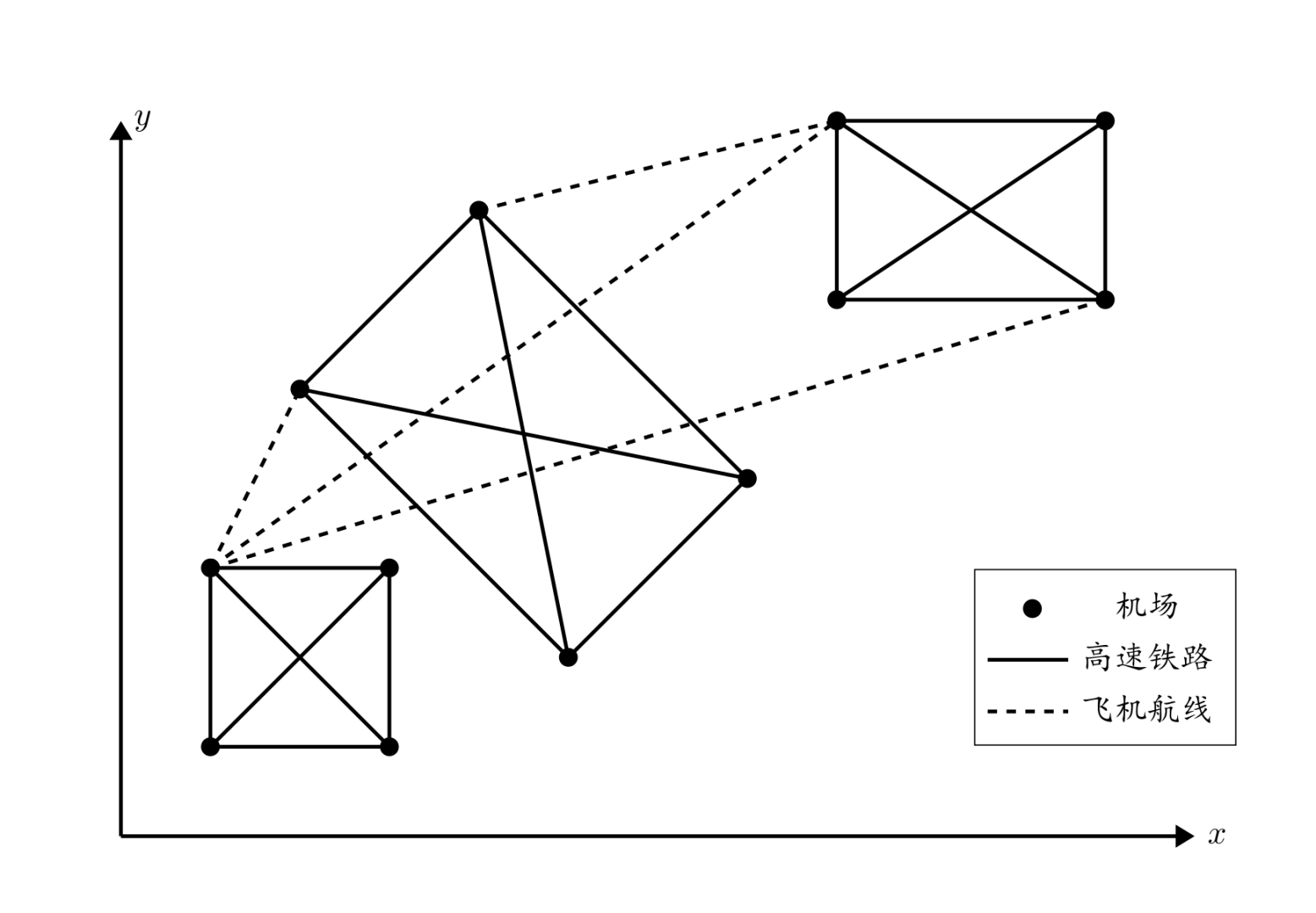
![](https://cdn.luogu.com.cn/upload/image_hosting/odqxn9sz.png)

**注意**：图中并没有标出所有的铁路与航线。

那么 Car 应如何安排到城市 B 的路线才能尽可能的节省花费呢？她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市 A 到 B 的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

## 输入格式

第一行为一个正整数 $n$，表示有 $n$ 组测试数据。

每组的第一行有 $4$ 个正整数 $S,t,A,B$。

$S$ 表示城市的个数，$t$ 表示飞机单位里程的价格，$A$，$B$ 分别为城市A，B 的序号。

接下来有 $S$ 行，其中第 $i$ 行均有 $7$ 个正整数$x_{i1},y_{i1},x_{i2},y_{i2},x_{i3},y_{i3},T_i$，这当中的 $(x_{i1},y_{i1}), (x_{i2},y_{i2}), (x_{i3},y_{i3})$，分别是第 $i$ 个城市中任意 $3$ 个机场的坐标，$T_i$ 为第 $i$ 个城市高速铁路单位里程的价格。

## 输出格式

共有 $n$ 行，每行 $1$ 个数据对应测试数据。
保留一位小数。

## 输入输出样例 #1

### 输入 #1

```
1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3
```

### 输出 #1

```
47.5
```

## 说明/提示

【数据范围】
对于 $100\%$ 的数据，$1\le n \le 10$，$1\le S \le 100$，$1\le A,B \le S$。

**【题目来源】**

NOIP 2001 提高组第四题

#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <iomanip>
#include <climits>using namespace std;// 定义点的结构体，包含x和y坐标
struct Point {double x, y;Point(double x = 0, double y = 0) : x(x), y(y) {}
};// 计算两点之间的欧几里得距离
double distance(const Point& p1, const Point& p2) {double dx = p1.x - p2.x;double dy = p1.y - p2.y;return sqrt(dx * dx + dy * dy);
}// 根据给定的三个点，找到矩形的第四个顶点
Point findFourthPoint(const Point& p1, const Point& p2, const Point& p3) {// 计算三个点之间的平方距离，避免浮点精度问题double d12 = (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);double d13 = (p1.x - p3.x) * (p1.x - p3.x) + (p1.y - p3.y) * (p1.y - p3.y);double d23 = (p2.x - p3.x) * (p2.x - p3.x) + (p2.y - p3.y) * (p2.y - p3.y);// 确定直角点，然后计算第四个点if (d12 > d13 && d12 > d23) {// p1和p2是对角线，p3是顶点，第四个点是p1 + p2 - p3return Point(p1.x + p2.x - p3.x, p1.y + p2.y - p3.y);} else if (d13 > d12 && d13 > d23) {// p1和p3是对角线，p2是顶点，第四个点是p1 + p3 - p2return Point(p1.x + p3.x - p2.x, p1.y + p3.y - p2.y);} else {// p2和p3是对角线，p1是顶点，第四个点是p2 + p3 - p1return Point(p2.x + p3.x - p1.x, p2.y + p3.y - p1.y);}
}// Dijkstra算法求最短路径
double dijkstra(const vector<vector<pair<int, double>>>& graph, int start, int end) {int n = graph.size();vector<double> dist(n, INT_MAX); // 初始化所有距离为无穷大dist[start] = 0; // 起点到自身的距离为0// 使用优先队列（最小堆）来优化查找当前距离最小的节点priority_queue<pair<double, int>, vector<pair<double, int>>, greater<pair<double, int>>> pq;pq.push({0, start});while (!pq.empty()) {double current_dist = pq.top().first;int u = pq.top().second;pq.pop();// 如果当前距离大于已知距离，跳过if (current_dist > dist[u]) continue;// 遍历当前节点的所有邻居for (const auto& edge : graph[u]) {int v = edge.first;double cost = edge.second;// 如果通过当前节点u到达v的距离更短，则更新距离if (dist[v] > dist[u] + cost) {dist[v] = dist[u] + cost;pq.push({dist[v], v});}}}return dist[end]; // 返回到达终点的最短距离
}int main() {int n;cin >> n; // 读取测试数据组数while (n--) {int S, t, A, B;cin >> S >> t >> A >> B; // 读取城市数、飞机单位价格、起始城市、目标城市A--; // 转换为0-based索引B--;vector<vector<Point>> airports(S); // 每个城市的四个机场坐标vector<double> T(S); // 每个城市的铁路单位价格// 读取每个城市的三个机场坐标和铁路单位价格，并计算第四个机场坐标for (int i = 0; i < S; i++) {double x1, y1, x2, y2, x3, y3;cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3 >> T[i];Point p1(x1, y1), p2(x2, y2), p3(x3, y3);Point p4 = findFourthPoint(p1, p2, p3);airports[i] = {p1, p2, p3, p4};}// 构建图，每个机场的编号为 city * 4 + airport_idxint num_nodes = S * 4;vector<vector<pair<int, double>>> graph(num_nodes);// 添加同一城市内的铁路边for (int city = 0; city < S; city++) {for (int i = 0; i < 4; i++) {for (int j = i + 1; j < 4; j++) {double dist = distance(airports[city][i], airports[city][j]);double cost = T[city] * dist;int u = city * 4 + i;int v = city * 4 + j;graph[u].push_back({v, cost});graph[v].push_back({u, cost});}}}// 添加不同城市之间的航线边for (int city1 = 0; city1 < S; city1++) {for (int city2 = city1 + 1; city2 < S; city2++) {for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {double dist = distance(airports[city1][i], airports[city2][j]);double cost = t * dist;int u = city1 * 4 + i;int v = city2 * 4 + j;graph[u].push_back({v, cost});graph[v].push_back({u, cost});}}}}// 计算从起始城市A的四个机场到目标城市B的四个机场的最短路径double min_cost = INT_MAX;for (int i = 0; i < 4; i++) {for (int j = 0; j < 4; j++) {int start = A * 4 + i;int end = B * 4 + j;double cost = dijkstra(graph, start, end);if (cost < min_cost) {min_cost = cost;}}}// 输出最小花费，保留一位小数cout << fixed << setprecision(1) << min_cost << endl;}return 0;
}