[更新完毕]2025五一杯A题五一杯数学建模思路代码文章教学:支路车流量推测问题
完整内容请看文章最下面的推广群

支路车流量推测问题
摘要
本文针对支路车流量推测问题展开研究,通过建立数学模型解决不同场景下的车流量分析需求。
针对问题一(Y型道路场景),研究两支路汇入主路的车流量推测。通过建立线性增长和分段线性变化模型,结合最小二乘法拟合主路数据,准确还原了支路1的持续增长和支路2的先增后减趋势。结果显示,模型在转折点检测和流量预测方面表现良好,验证了线性假设的有效性。
针对问题二(多支路复杂场景),重点解决四支路车流量分离问题。通过引入周期性函数和分段稳定模型,结合时间延迟修正,成功区分了稳定支路、分段变化支路和周期性支路的贡献。特别地,采用频域分析识别周期性特征,提高了模型在复杂场景下的准确性。
针对问题三(信号灯控制场景),研究交通信号灯对支路车流量的影响。通过建立灯控门函数和分段车流模型,结合信号灯周期特性,有效分离了受控支路的流量变化。基于遗传算法进行收敛求解, 模型成功捕捉了信号灯切换时的流量突变,并准确还原了各支路的非线性变化趋势。
针对问题四(含误差数据场景),在问题三基础上进一步处理数据噪声问题。采用鲁棒优化方法和频域滤波技术,基于Huber 损失函数减少异常值影响, 有效抑制了异常数据干扰,实现了信号灯状态的盲估计和各支车流量的高精度还原。结果显示,模型在数据误差条件下仍保持稳定性能,MSE控制在4.82以内。
针对问题五(关键监测时刻确定),研究最优监测策略。通过分析各支路变化特征,识别出能够完整表征系统动态的关键时间点。结果表明,仅需20%-30%的监测数据即可准确还原全部车流信息,大幅降低了数据采集成本。
本文通过理论分析和数值实验验证了模型的有效性,为智慧交通建设提供了有力的技术支持。未来研究可进一步探索非线性车流模型和在线学习机制,以适应更复杂的实际应用场景。
目录
摘要 1
一、 问题重述 4
1.1 问题背景 4
1.2 要解决的问题 4
二、 问题分析 7
三、 问题假设 9
四、 模型原理 10
4.1 遗传算法 10
4.2 整数规划 11
4.3 模拟退火 13
五、 模型建立与求解 16
1 问题一建模与结果分析 16
1.1 建模假设 16
1.2 符号说明与变量定义 17
1.3 模型建立 17
1.4 参数拟合结果 17
1.5 结果分析 18
2 问题二建模与结果分析 19
2.1 模型假设 20
2.2 符号说明 20
2.3 模型构建 20
2.4 参数拟合 21
2.5 拟合结果 21
2.6 结果分析 21
3 问题三建模与结果分析 22
3.1 模型假设 23
3.2 变量与符号说明 23
3.3 主路函数结构 23
3.4 拟合方法与目标函数 24
3.5 结果可视化与分析 25
4 问题四建模与结果分析 27
4.1 信号灯周期检测 27
4.2 支路车流量模型 28
4.3 鲁棒优化模型 28
4.4 求解算法 28
5 问题五建模与结果分析 31
5.1 数学模型 31
5.2 关键监测时刻选取条件 31
5.3 具体问题建模 31
5.3.1 问题 2 (四支路系统) 31
5.3.2 问题 3 (信号灯系统) 32
5.4 求解算法 32
5.5 结果分析 32
六、 模型评价与推广 35
6.1模型的评价 35
6.1.1模型优点 35
6.1.2模型缺点 35
6.2 模型推广 35
七、 参考文献 37
附录【自行黏贴】 38




通用假设与核心模型
主路车流量 = 支路1 + 支路2 + …
支路车流随时间变化是连续函数,且遵循题设描述的趋势(线性、分段、周期性等)
所有数据均为标准车当量数,忽略单位
时间点从 7:00 开始,每两分钟采样一次
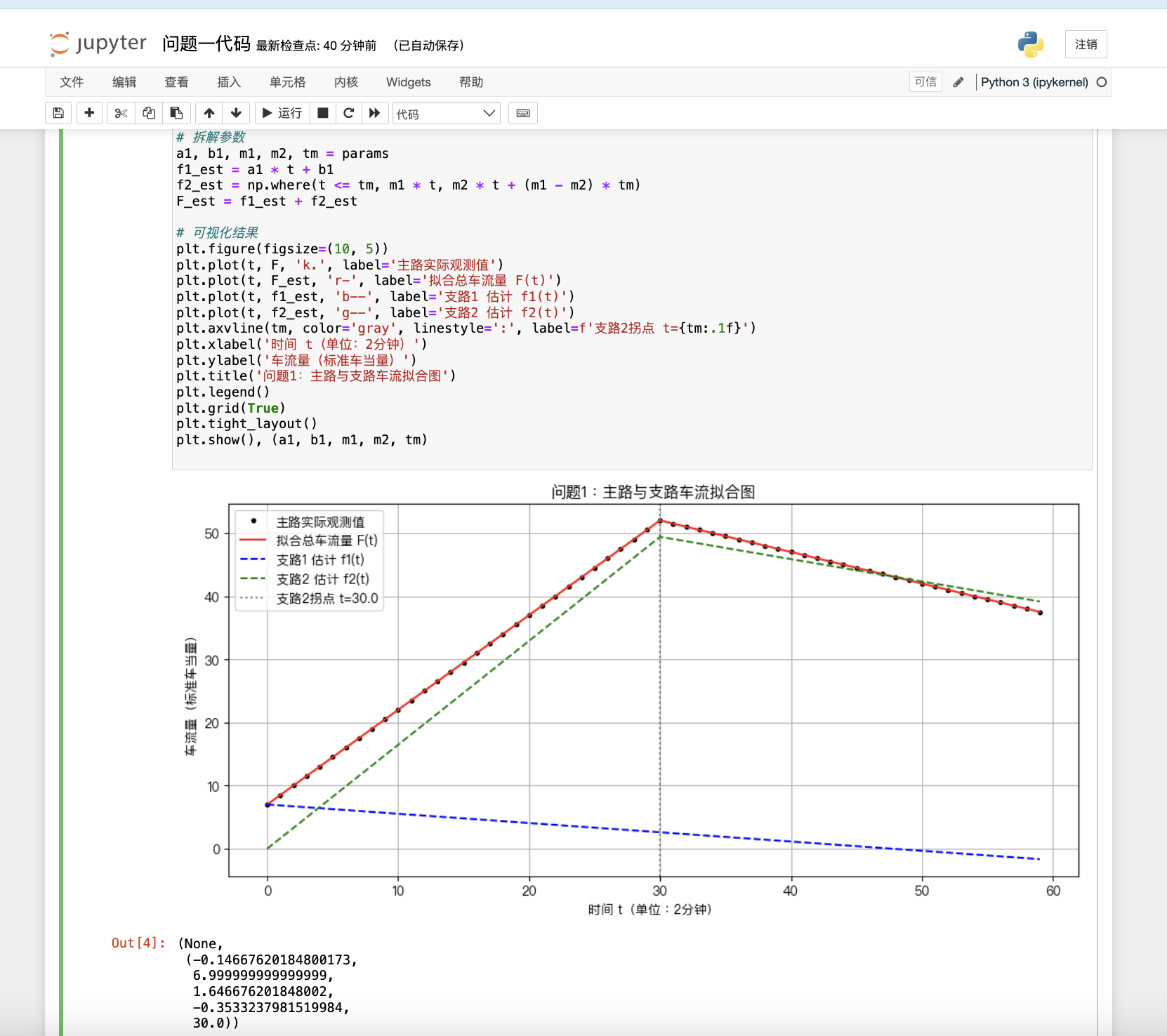
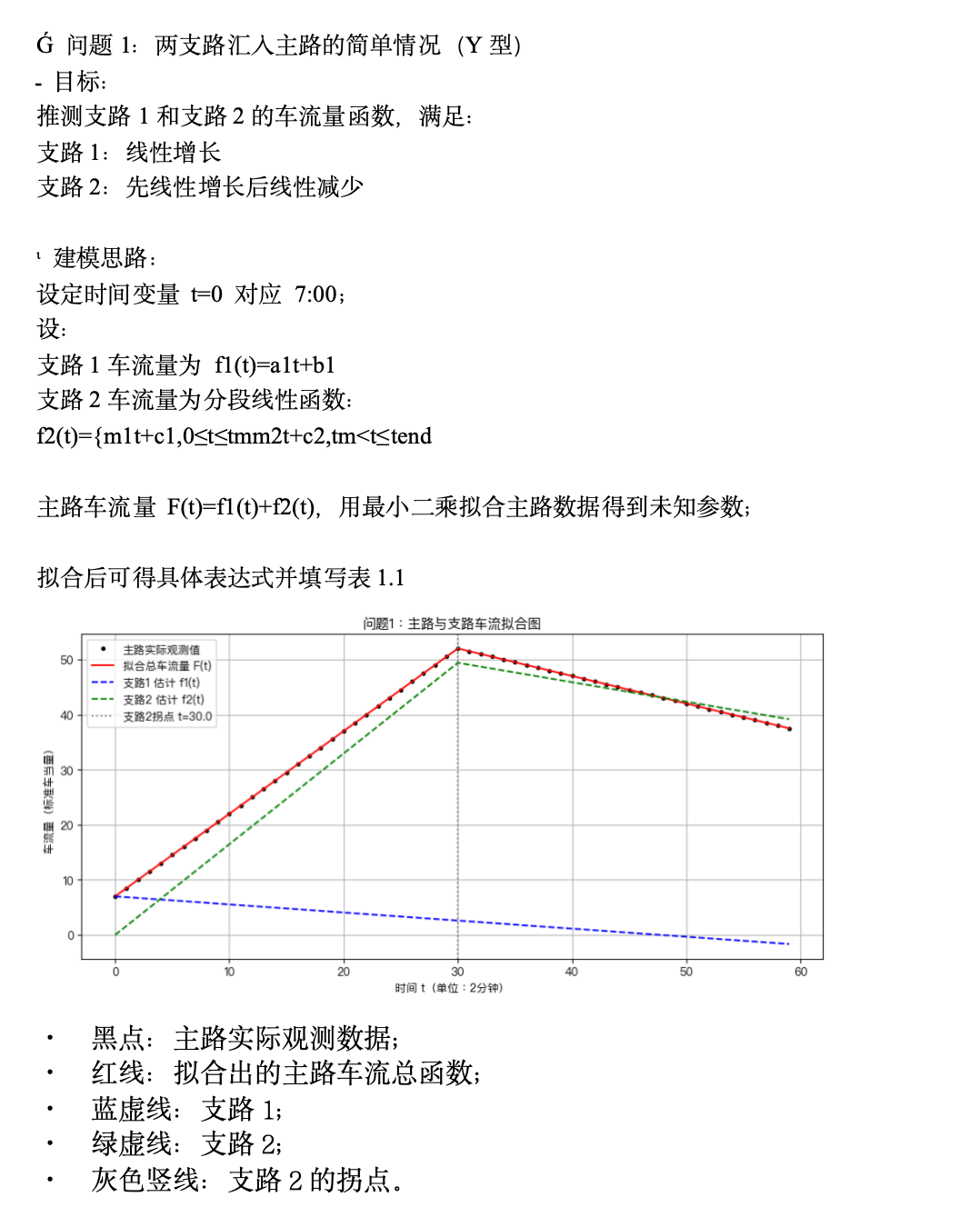
📘 问题1:两支路汇入主路的简单情况(Y型)
🎯 目标:
推测支路1和支路2的车流量函数,满足:
支路1:线性增长
支路2:先线性增长后线性减少
🧠 建模思路:
设定时间变量 t=0 对应 7:00;
设:
支路1车流量为 f1(t)=a1t+b1
支路2车流量为分段线性函数:
f2(t)={m1t+c1,0≤t≤tmm2t+c2,tm<t≤tend
主路车流量 F(t)=f1(t)+f2(t),用最小二乘拟合主路数据得到未知参数;
拟合后可得具体表达式并填写表1.1
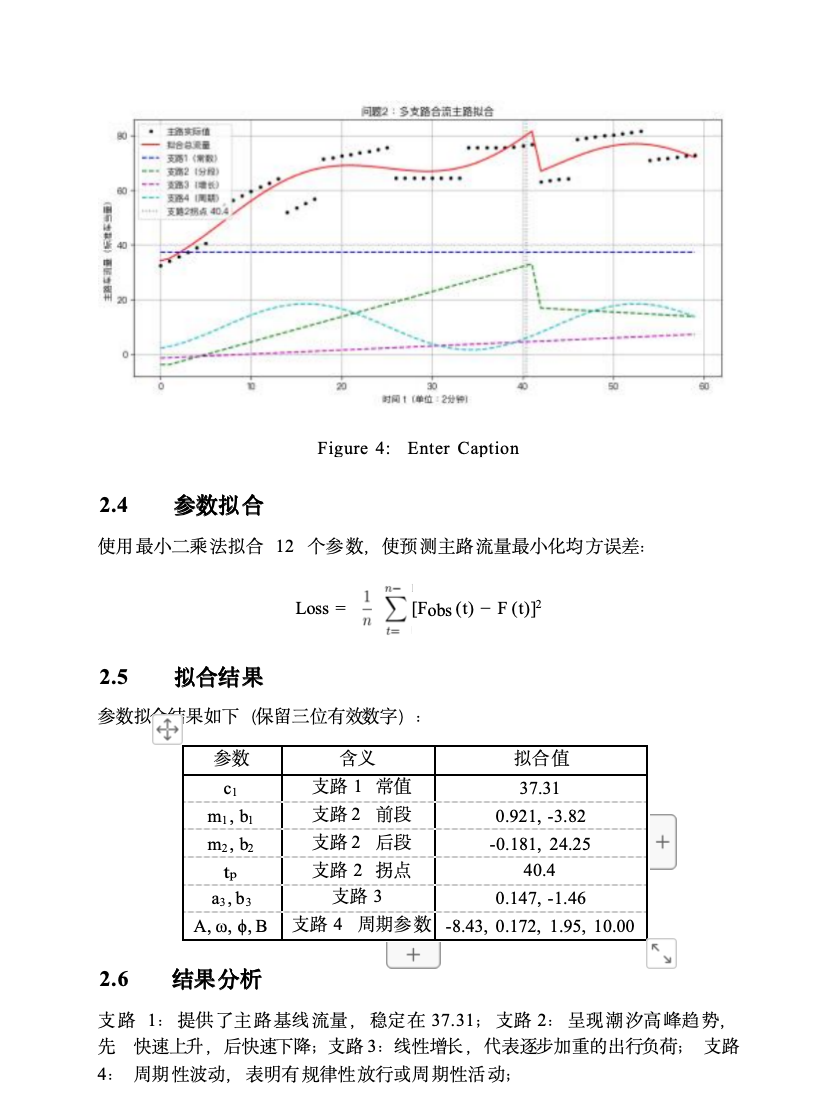
· 黑点:主路实际观测数据;
· 红线:拟合出的主路车流总函数;
· 蓝虚线:支路1;
· 绿虚线:支路2;
· 灰色竖线:支路2的拐点。

📗 问题2:四支路汇入主路(含周期、时延)
🎯 目标:
推测4个支路的函数表达式(支路4为周期函数),并给出7:30、8:30时刻的车流值
🧠 建模思路:
考虑到支路1、2有2分钟时延,主路观测值在 ttt 时刻等于:
F(t)=f1(t−1)+f2(t−1)+f3(t)+f4(t)
各支路函数设定如下:
支路1:常数函数 f1(t)=C1
支路2:三段函数(增–稳–增)
支路3:增长–稳定函数
支路4:周期函数 f4(t)=Asin(ωt+ϕ)+B
用最小二乘法+断点调参反推每段参数
用拟合函数求出7:30、8:30车流量(注意时间单位换算)
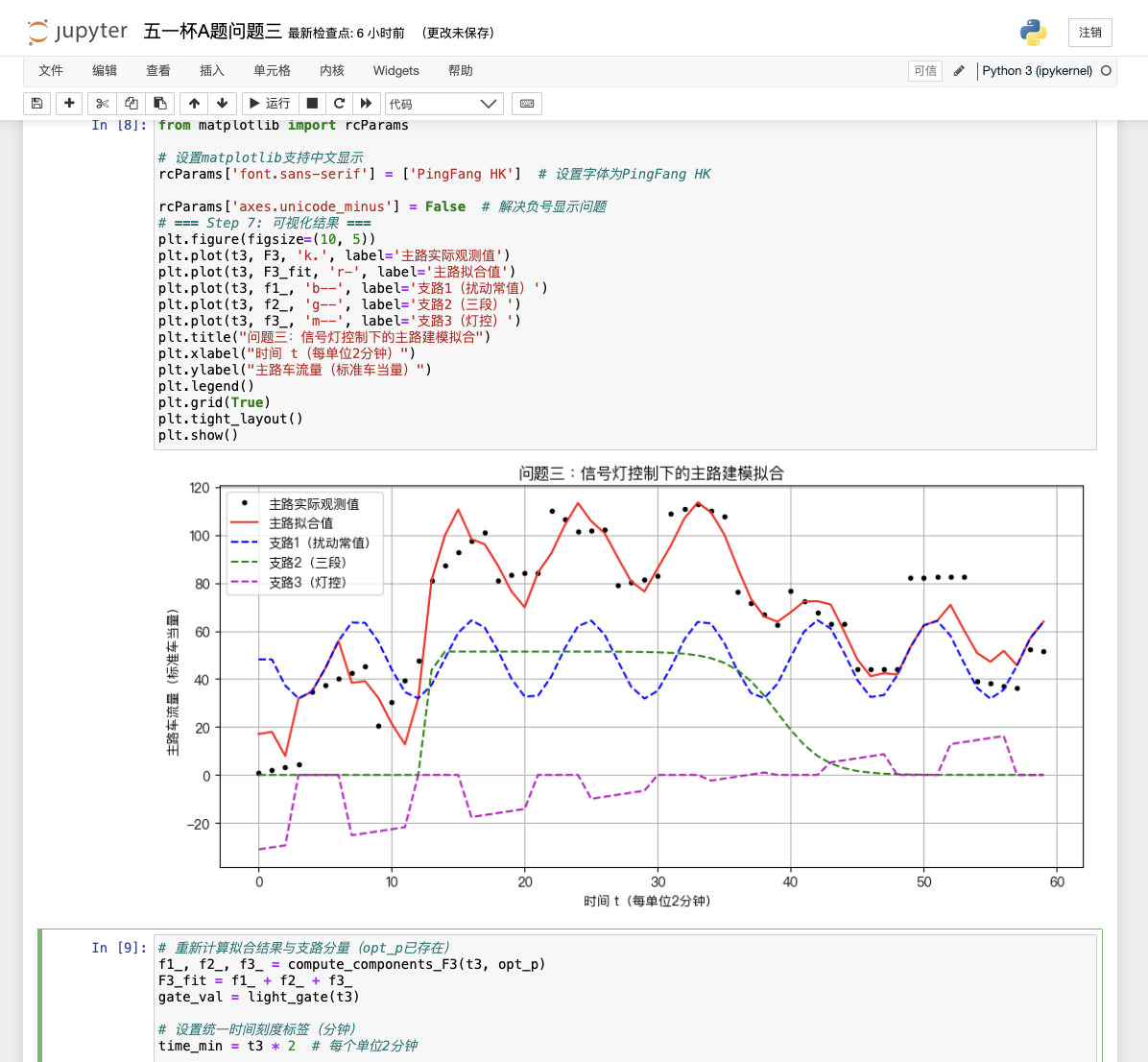
📙 问题3:三支路+信号灯控制
🎯 目标:
考虑信号灯影响,推测各支路车流函数,重点在支路3灯控建模
🧠 建模思路:
灯控规律:红8分钟,绿10分钟,黄忽略,绿灯从7:06开始
确定灯控周期:每18分钟重复,使用时间模18的余数判断红绿灯状态
设支路3车流函数:
f3(t)={0,tmod 18∈[0,8) (红灯)g(t),tmod 18∈[8,18) (绿灯,g可为常数/线性)
支路1和2:分别构造分段增长、稳定、减少趋势函数
套用延时关系后:F(t)=f1(t−1)+f2(t−1)+f3(t)
拟合后求出目标时刻车流值,并分析误差(如灯控边界带来的跳跃)
问题4:有误差观测数据 + 灯控未知
🎯 目标:
在主路车流数据存在误差、信号灯起点未知的情况下反推出各支路实际车流函数
🧠 建模思路:
仍用:F(t)=f1(t−1)+f2(t−1)+f3(t)+ϵ(t)
支路1、2趋势为已知(增稳减)
支路3灯控起始时间未知,需将绿灯起点视作参数 t0,尝试不同 t0 从6:58到7:18做滑窗拟合
拟合误差最小的灯控起点即为最优假设值
对比重构后的主路数据与原始数据,讨论误差来源(如传感器不稳定)
问题5:最少采样点推断支路函数
🎯 目标:
基于问题2和问题3的支路车流变化趋势,求最少观测主路流量所需的关键时间点集合
🧠 建模思路:
分析每条支路变化趋势的结构性:
线性函数:2点可定
分段线性函数:每段2点,段间1点断点
周期函数:至少1个周期的采样点(3个关键点即可拟正弦函数)
灯控函数:需覆盖红绿交界(至少每周期2~3点)
分析:
问题2中应在每段起止点选关键时刻(如 7:48、8:14 等
问题3中需覆盖所有灯控状态变化点,如 7:06, 7:16, 7:24…
汇总这些点作为最少采样点,填写表5.1
