当前位置：首页 > news >正文

AVL树左旋右旋的实现

news 来源：原创 2025/4/30 6:13:06

AVL树的实现

1.节点的实现

2.AVL树的基本结构

3.基本原理

4.旋转的分类

5.代码实现

LL型

RR型

AVL树的实现

1.节点的实现

在实现左旋和右旋之前，我们先写一个AVL树的节点，由于加入了平衡因子的概念，所以我们在节点中要存入父节点和平衡因子。

template<class K, class V>
struct AVLTreeNode
{// 需要parent指针，后续更新平衡因子可以看到pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}//AVL树的节点
};

2.AVL树的基本结构

AVL树我们存入一个_root就可以找到所有的子树，所以私有变量给-root根节点。下面给出AVL的基本结构。

template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:private:private:Node* _root = nullptr;
};

3.基本原理

我们知道，AVL树和二叉搜索树的最根本区别是AVL树必须保持高度平衡搜索效率稳定，二叉搜索树在极端条件搜索效率退化到LOG N，我们这里就要知道AVL树是怎么控制平衡的，答案就是旋转，那我们就得知道什么时候旋转，所以我们引入了平衡因子的概念，它的大小等于右子树的高度减去左子树的高度，平衡状态下，它的值为-1,1或0，当出现2时说明这颗树该更新了，那么我们插入一个节点的时候，如果它的平衡因子没有2或-2我们就不用更新，一旦出现了2或-2，从出现2或-2的位置开始更新。

4.旋转的分类

了解了基本原理之后，我们来对旋转进行基本的分类，我把它分为LL型，LR型，RR型,RL型，这里我们解释一下，LL型就是左子树的左边高，对它进行右旋，LR型是左子树的右边高，先左旋左孩子，再右旋，RR型是右子树的右边高，对它进行左旋，RL型是右子树的左边高，先右旋右孩子，再左旋。本质就是把它的高度压低。

这个是RL型，先右旋15，再左旋10.

这个是LR型，先左旋5，再右旋10

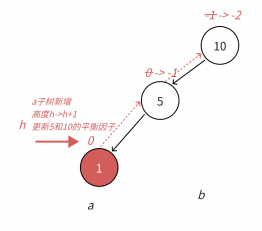这个是LL型，右旋10.

这个是RR型，左旋10.

5.代码实现

理论已经就位了，那么我们该怎么实现呢？

首先我们要解决的是怎么识别它们的类型，先从简单的LL型和RR型说起，借助上面的图片我们可以知道：

1.当一个节点的平衡因子在插入后更新为2或-2，然后判断它的左子树左边高，我们对它进行判定为LL型，对平衡因子为2的节点进行右旋。

2.当一个节点更新为2或-2后，它的右子树的右边高我们对它进行判断为RR型。

3，当左节点的右子树高，判断为LR型。

3.当右节点的左子树高，判定为RL型。

下面是代码判断，由于左子树失衡，所以_BF为-2，又因为是左子树的左节点高，所以CUR=-1。条件满足，进行右旋。

LL型

	if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}

这里具体实现时需要注意几个点，由于我们不知道这个调整的节点是根节点还是叶子节点，所以我们需要根据它的父亲对它进行判断，如果父亲是空，调整的节点就是根节点，不然就是叶子节点，需要改父亲。还有就是我们不知道需要调整的节点的左子树的右子树是否为空，需要对它进行判断。最后就是更改节点的指向时，记得也更改它的父亲节点。

	void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}subL->_bf = parent->_bf = 0;}

RR型

if(parent->bf==2&&parent->right->bf==1)
{//进行左旋
}

同样的需要注意和右旋类似的事情。

	void RotateL(Node* parent){/*Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}parent->_bf = subR->_bf = 0;*/auto ppnode = parent->_parent;//保存调整节点的父节点。auto subr = parent->_right;auto subrl = subr->_left;if (subrl != nullptr){parent->_right = subrl;subrl->_parent = parent;subr->_left = parent;parent->_parent = subr;if (ppnode == nullptr){subr->_parent = nullptr;_root = subr;}else if (ppnode != nullptr){subr->_parent = ppnode;}}else if (subrl == nullptr){parent->_right = subrl;subr->_left = parent;parent->_parent = subr;if (ppnode == nullptr){subr->_parent = nullptr;_root = subr;}else if (ppnode != nullptr){subr->_parent = ppnode;}}parent->_bf = subr->_bf = 0;}

至于RL型和LR型，我们一篇博客再见，如有错误请多指正，博主十分感激！！！