【漫话机器学习系列】224.双曲正切激活函数(Hyperbolic Tangent Activation Function)
双曲正切激活函数(tanh)详解:更优于 Sigmoid 的选择?
在构建神经网络时,激活函数是非常关键的一环。本文将带大家深入了解一种常见但常被忽视的激活函数:双曲正切函数(Hyperbolic Tangent Function,简称 tanh)。通过图解和数学表达,我们来剖析它的性质及在实际中的应用。
一、什么是双曲正切函数(tanh)?
双曲正切函数(tanh) 是一种 S 形的激活函数,其数学表达形式为:
它是通过双曲正弦(sinh)与双曲余弦(cosh)的比值得到的函数,图像如下所示:
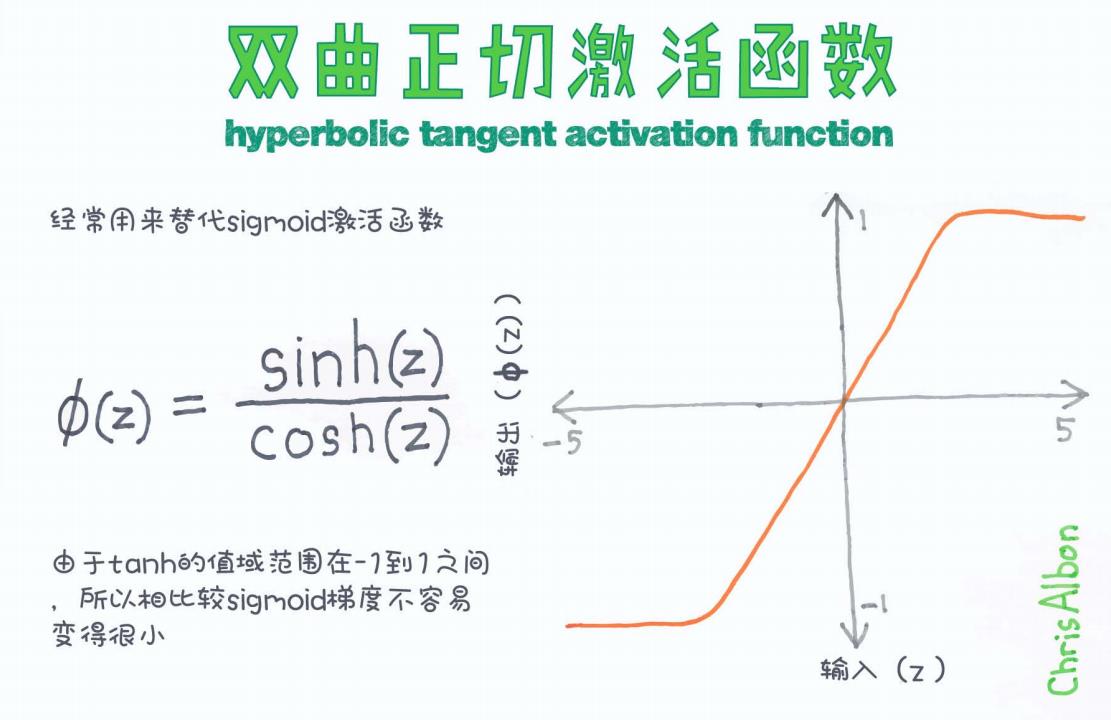
二、tanh 与 sigmoid 有什么区别?
虽然 tanh 和 sigmoid 都是 S 型函数,但它们的输出范围不同:
| 函数 | 输出范围 | 是否中心化 | 常见问题 |
|---|---|---|---|
| sigmoid | (0, 1) | 否 | 梯度消失问题严重 |
| tanh | (-1, 1) | 是 | 梯度问题缓解 |
为什么 tanh 更推荐?
从图中我们可以看出,tanh 函数的输出是以 0 为中心的对称区间 [-1, 1],相比 sigmoid 更接近“0 中心化”。这意味着,在使用 tanh 激活函数时,神经元的输出会更容易让下一层网络保持平衡的输入分布,从而加快收敛速度。
而 sigmoid 的输出全为正(0 到 1),可能导致后续层输出出现偏移,从而增加训练难度。
三、tanh 的图像分析
从图像中可以观察到:
-
当输入 z → −∞ 时,输出趋近于 -1;
-
当输入 z → +∞ 时,输出趋近于 +1;
-
在 z = 0 时,输出正好为 0;
-
整体是光滑、连续且可导的函数,适合用于反向传播计算。
四、tanh 的导数
tanh 函数的导数形式非常简单:
这是它相较于 sigmoid 的另一大优势,便于梯度的传播计算。
五、在深度学习中的应用场景
虽然 ReLU 类函数现在是主流,但 tanh 依然有其重要应用:
-
用于处理有负值输入的数据;
-
适用于较浅层网络,或需要输出在 [-1, 1] 区间的模型;
-
在 LSTM 等循环神经网络中依然广泛使用(如门控机制中就大量采用 tanh)。
六、总结
| 特性 | tanh |
|---|---|
| 输出范围 | (-1, 1) |
| 是否0中心化 | 是 |
| 是否可导 | 是 |
| 梯度问题 | 相较 sigmoid 更缓和 |
| 应用领域 | 循环神经网络(LSTM)、二分类模型等 |
小结:
tanh 是一个简单却非常强大的激活函数,虽然近年来被 ReLU 抢去了风头,但它仍在很多模型中扮演着关键角色。选择激活函数时,没有“放之四海皆准”的标准,重要的是根据你的问题和数据类型合理选择。
