【状态空间方程】对于状态空间方程矩阵D≠0时的状态反馈与滑模控制
又到新的一年啦，2025新年快乐~。前几个月都没更新，主要还是因为不能把项目上的私密工作写进去，所以暂时没啥可写的。最近在山里实习，突然想起年前遗留了个问题一直没解决，没想到这两天在deepseek的加持下很快解决了，只能说AI还是猛，能提供很好的建议。
0. 问题描述
作为一个控制人，最常见的模型表达式莫过于状态空间方程和二阶的非线性方程了：
对于绝大多数情况下，上述状态空间方程中的前馈矩阵D一般为0，即输入一般不直接影响输出，但是最近遇到个问题，其辨识出来的模型中矩阵D不为0，然后让你去控制它，这种情况我还真第一次遇到，当我尝试使用最简单的滑模控制来设计控制器时却遇到了问题，并且随后发现了更大的奥秘…
问题总结：对于前馈矩阵D≠0的情况，如何设计状态反馈或滑模控制器？
1. 状态反馈控制
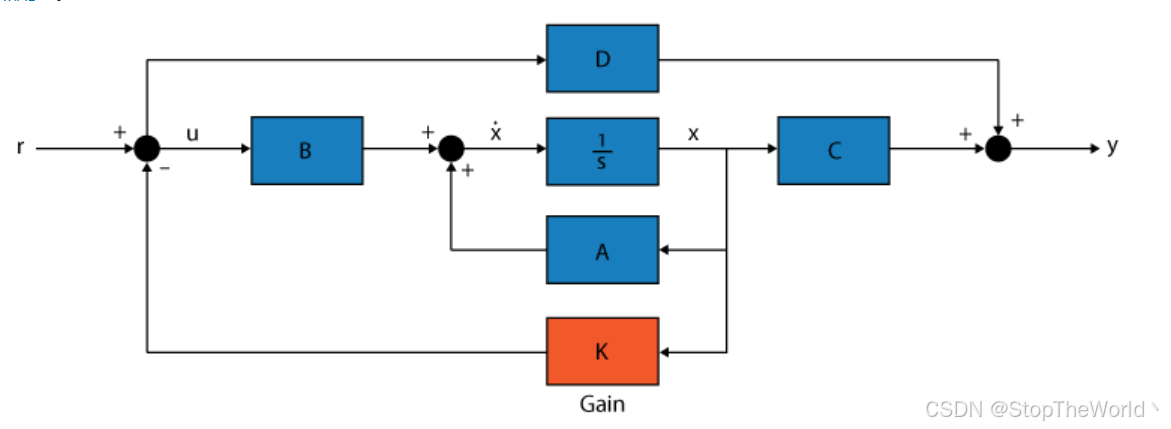
状态反馈控制通过反馈状态变量来设计控制器，即使 D≠0，状态反馈控制律仍可以设计为
u
=
−
K
x
u=-Kx
u=−Kx 的形式。matlab提供了place函数，可直接进行极点配置得到反馈增益矩阵K。
若状态变量不可测时，可使用输出反馈控制，输出反馈控制律为
u
=
−
K
y
u=-Ky
u=−Ky，其中
y
=
C
x
+
D
u
y=Cx+Du
y=Cx+Du。
注：place函数适用于多输入多输出系统，而acker函数仅用于单输入系统。
仿真验证
以倒立摆系统为例，人为的让矩阵D不为0，验证状态反馈控制，以下为系统输出变量y的变化曲线，可以看出，即使对于D≠0的情况，状态反馈控制仍然具有良好的控制效果。
2. 滑模控制
为了考虑D≠0的影响，最开始是想设计滑模面 s = S x + K y s=Sx+Ky s=Sx+Ky 的形式，并采用等效控制和切换控制的方式 u = u e q + u s w u=u_{eq}+u_{sw} u=ueq+usw 设计控制律，不过后续发现无论如何调整设计矩阵S和K的参数，均不能完成控制。期间学到了在对y求导时，控制输入u的导数du可以适当忽略，原因如下：
- 控制输入的动态特性：在实际系统中，执行器的动态特性通常比系统的动态特性快得多，即执行器的响应时间远小于系统的时间常数。因此， u ˙ \dot{u} u˙ 的影响可以忽略不计。
- 滑模控制的鲁棒性：滑模控制的核心思想是通过高频切换控制律（如符号函数 sign(s(x))）来驱动系统状态到达滑模面并保持在滑模面上。这种高频切换本身就具有很强的鲁棒性，能够克服系统中的不确定性和扰动。即使 u ˙ \dot{u} u˙ 存在，其影响也会被滑模控制的鲁棒性所抑制。
- 简化设计过程：忽略 u ˙ \dot{u} u˙ 可以大大简化控制律的设计过程。如果考虑 u ˙ \dot{u} u˙，控制律的设计会变得非常复杂，尤其是在多输入多输出（MIMO）系统中。通过忽略 u ˙ \dot{u} u˙，可以将问题简化为一个静态反馈控制问题，从而更容易设计控制器。
- 实际系统的验证：在实际系统中，忽略 u ˙ \dot{u} u˙ 的假设通常可以通过仿真和实验验证。如果仿真和实验结果表明系统的性能满足要求，那么这一假设就是合理的。
特殊情况下的处理：如果 u ˙ \dot{u} u˙ 的影响确实不可忽略（例如，执行器的动态特性较慢），可以通过以下方法处理：① 引入动态扩张：将 u 视为一个新的状态变量，设计扩张状态空间方程。② 高阶滑模控制：设计高阶滑模控制器，直接考虑 u ˙ \dot{u} u˙ 的影响。
解决方案：由于联合设计参数
S
S
S 和
K
K
K 没有成功，因此这里将滑模面设计为仅与状态变量有关的形式
s
=
S
x
s=Sx
s=Sx ，并采用极点配置法计算参数
S
S
S。对于单输入系统，采用Ackermann公式设计参数
S
S
S：
S
=
[
0
,
0
,
.
.
.
,
1
]
⏟
n
维
[
B
,
A
B
,
A
2
B
,
.
.
.
,
A
n
−
1
B
]
−
1
(
A
−
λ
1
∗
e
y
e
(
n
)
)
∗
(
A
−
λ
2
∗
e
y
e
(
n
)
)
.
.
.
∗
(
A
−
λ
n
−
1
∗
e
y
e
(
n
)
)
S=\underset{n\text{维}}{\underbrace{\left[ 0,0,...,1 \right] }}\left[ B,AB,A^2B,...,A^{n-1}B \right] ^{-1}\left( A-\lambda _1*eye\left( n \right) \right) *\left( A-\lambda _2*eye\left( n \right) \right) ...*\left( A-\lambda _{n-1}*eye\left( n \right) \right)
S=n维
[0,0,...,1][B,AB,A2B,...,An−1B]−1(A−λ1∗eye(n))∗(A−λ2∗eye(n))...∗(A−λn−1∗eye(n))其中
λ
1
,
λ
2
,
.
.
.
λ
n
−
1
\lambda _1,\lambda _2,...\lambda _{n-1}
λ1,λ2,...λn−1是滑模面的期望极点，之所以最后下标是n-1而不是n，是因为滑模面 s(x) = 0 是一个超平面，其维度比原系统的状态空间维度低一维（即 n-1 维）。
仿真验证
同样的，以倒立摆系统为例，验证滑模控制，观测系统的输出变量y，可以看出，即使对于D≠0的情况，滑模控制依然具有较好的控制效果，但明显不如状态反馈平滑，且伴随轻微抖振情况。
3. C≠单位阵时的线性变换
上述解决了矩阵D≠0的情况，此外当D=0时还存在一种情况，即C不等于单位矩阵，此时需要采用线性变换进行处理，即 { A ′ = T − 1 A T B ′ = T − 1 B C ′ = C T \begin{cases} A^{\prime}=T^{-1}AT\\ B^{\prime}=T^{-1}B\\ C^{\prime}=CT\\ \end{cases} ⎩ ⎨ ⎧A′=T−1ATB′=T−1BC′=CT其中， C ′ C^{\prime} C′ 为变换后的单位阵，并可解出满足条件的任一变换矩阵 T T T，随后得到变换后的 A 、 B A、B A、B 矩阵。
4. 总结
基于以上结论，总结如下：
- 虽然可通过状态变换消去D，但是会引入新的状态变量，所以视情况处理D的影响。
- 对于D≠0时的状态反馈控制以及滑模控制，大多数情况下可以不考虑D的影响，仍然采用状态变量反馈控制即可，少数情况下需要考虑输出D的影响；
- 对于控制输入u的导数影响可以适当忽略，实在不能忽略的话可设计高阶滑模控制器或扩张状态空间方程来考虑u；
- 善用AI工具，用批判的眼光看待它给出的答案（deepseek还是好用）。