Kaggle竞赛——商店销售时序预测（Store Sales）

总述

竞赛的任务是基于以往的时序数据来预测未来15天销售额，需要从给定的数据集中分析并提取有价值的特征。可视化分析发现每日油价与每日平均销售额的相关系数为 -0.6269，呈负相关，因此可将每日油价数据合并到训练集中。通过趋势分析发现平均销售额整体呈线性上升趋势，根据趋势特征选择线性回归模型来拟合趋势。节假日分析表明节假日和非节假日的销售额之间分层明显，节假日的销售额整体大于非节假日的销售额，因此将判断是否为节假日的特征列并入训练集以区分节假日和非节假日。由于订单量数据仅包含在训练集中，因此仅进行数据分析，不做特征处理。数据处理完成后利用线性回归拟合 DeterministicProcess 生成的线性特征数据（趋势特征、季节性特征（短期）和傅里叶特征（长期）），并利用 CATBoost 模型拟合真实值与线性模型预测值之间的残差值。最终提交的预测结果得分（RMSLE）为0.72345。源码已上传至Gitee（数据集较大未上传），点击直达。

1. 竞赛介绍

此竞赛是关于商店销售的时间序列预测，数据来自一家名为 Corporación Favorita 的厄瓜多尔公司，它是一家大型杂货零售商。此外，该公司还在南美洲的其他国家开展业务。本次比赛的主要任务是预测不同商店中不同产品系列的销售额。 数据集包含 54 家商店和 33 个产品系列，时间范围从 2013-01-01 到 2017-08-31 。数据集中包含的数据文件及字段描述如下：

---

test/train

• store_nbr: 商店标识
• family：销售的产品类型
• Sales: 各商店在给定日期的产品系列的总销售额
• onpromotion：各商店指定产品系列的商品促销量

stores：商店信息

• cluster：类似商店的组合

oil：每日油价

holidays_events：节假日信息

• date：日期
• type：类型
• locale：事件范围
• locale_name：事件范围的地点，如果是国家性的就对应厄瓜多尔，如果是某个地方的节日就对应某个地方
• description：节假日描述
• transferred：节日是否被转移，如果被转移，则需要找 type 列种值为 Transfer 的相应行来确定转移后的日期

transactions：商店订单数

---

测试数据中的日期是训练数据中最后一个日期之后的 15 天，即 2017-08-16 到 2017-08-31，数据集中不同文件的时间范围如下图所示。

2. 油价与销售额关系分析

数据导入：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')path = 'D:/Desktop/kaggle数据集/store-sales/'
# 将‘date’列转为日期（datetime）对象
oil = pd.read_csv(path+'oil.csv', parse_dates=['date'])
train = pd.read_csv(path+'train.csv', parse_dates=['date'])
test = pd.read_csv(path+'test.csv', parse_dates=['date'])
# samp_subm = pd.read_csv(path+'sample_submission.csv')
holiday = pd.read_csv(path+'holidays_events.csv', parse_dates=['date'])
store =  pd.read_csv(path+'stores.csv')
trans = pd.read_csv(path+'transactions.csv', parse_dates=['date'])

绘制油价变化图：

plot_params = dict(color="0.75", style=".-", markeredgecolor="0.25", markerfacecolor="0.25", legend=False)
ax = oil.set_index('date').plot(figsize = (10, 4))
ax.set_xlabel('Date')
ax.set_ylabel("Crude Oil");

绘制天/周/月的平均销售额变化图：

train_eda = train.copy() 
train_eda=train_eda.set_index('date') # resample('D'): 对索引按日进行重采样，索引需为时间序列类型
daily_sales=train_eda.resample('D').sales.mean().to_frame() 
weekly_sales=train_eda.resample('W').sales.mean().to_frame()  
monthly_sales=train_eda.resample('M').sales.mean().to_frame()  df=[daily_sales,weekly_sales,monthly_sales]
titles=['Daily Avg. Sales','Weekly Avg. Sales','Monthly Avg. Sales']for i,j in zip(df,titles):sns.relplot(x=i.index, y=i.sales,kind='line', aspect=3, hue=i.index.year)plt.xlabel('Date')plt.ylabel('Avg. Sales')plt.title(j)plt.show()

由每天的平均销售额变化图可知每年年初的销售额较低（接近0），这样看油价与销售额之间关系貌似不大，下面绘制相关性散点图来观察。

oil = oil.set_index('date')
# left_index=True,right_index=True：将索引设置为合并的键
# how='left': 左连接，即保留左边DataFrame（avg_sales）的所有行
train_oil=pd.merge(left=train_eda, right=oil, left_index=True, right_index=True, how='left')
# 列名重命名
train_oil.rename({'dcoilwtico':'oil_price'},axis=1,inplace=True)
#-----------------------------------------------------------------------------------------------------#
# fillna(method='ffill'): 使用前一个值填充缺失值
# fillna(method='bfill')：使用后一个值填充缺失值
#-----------------------------------------------------------------------------------------------------#
train_oil['oil_price']=train_oil['oil_price'].fillna(method='ffill').fillna(method='bfill')avg_sales = train_oil.groupby(['date','oil_price'])['sales'].mean().reset_index()
#-----------------------------------------------------------------------------------------------------#
# 计算两列特征的相关系数
# 相关系数矩阵是一个对称矩阵，对角线上的值为1，非对角线上的值表示不同变量间的相关系数
#-----------------------------------------------------------------------------------------------------#
print('每日平均销售额与每日油价的相关系数: ',np.round(avg_sales[['sales','oil_price']].corr().iloc[0,1],4),'\n')
plt.figure(figsize=(10,5))
sns.regplot(data=avg_sales, x='oil_price', y='sales', line_kws={'color':'red', 'linewidth':3})
plt.xlabel('Oil Price')
plt.ylabel('Avg. Sales')
plt.title('Avg. Sales vs. Oil Price')
plt.show()

输出：

每日平均销售额与每日油价的相关系数:  -0.6269

由图可知，每天的销售额与每日油价负相关，因为较低的油价意味着较低的生产成本，从而提高客户的购买力。此外，2015 年全年的销售额走势与油价走势接近。由于与销售额存在相关性，因此油价可作为并入训练集作为训练变量。

3. 各类商品销售情况

temp=train_eda.groupby('family')['sales'].mean().sort_values(ascending=False).to_frame()
plt.figure(figsize=(16,10))
sns.barplot(data=temp,x=temp.sales,y=temp.index,ci=None,order=list(temp.index), palette='rocket')
plt.xlabel('Avg. Sales')
plt.ylabel('Family Product')
plt.title('Avg. Sales by Family Product')
plt.show()print('销售额最高的5种商品: ',list(temp.index[:5]))
print('销售额最低的5种商品: ',list(temp.index[-5:]))

销售额最高的5种商品:  ['GROCERY I', 'BEVERAGES', 'PRODUCE', 'CLEANING', 'DAIRY']
销售额最低的5种商品:  ['MAGAZINES', 'HARDWARE', 'HOME APPLIANCES', 'BABY CARE', 'BOOKS']

由结果可知，销量最高的 5 种商品类型分别为杂货（grocery）、饮料（beverages）、农产品（produce）、清洁（cleaning）和乳制品（dairy）。

4. 不同时间尺度的销售额

以每日（周）/每月/每年为单位分析平均销售额的分布。

train_eda = train.copy() 
# 返回一周中的第几天，范围是 0（周一）到 6（周日）
train_eda['day']   = train_eda['date'].dt.dayofweek
# 返回日期的月份
train_eda['month'] = train_eda['date'].dt.month
# 返回日期的年份
train_eda['year']  = train_eda['date'].dt.yeardata_grouped_day = train_eda.groupby(['day'])['sales'].mean()
data_grouped_month = train_eda.groupby(['month'])['sales'].mean()
data_grouped_year = train_eda.groupby(['year'])['sales'].mean()plt.subplots(nrows=1, ncols=3, figsize=(20,5))
plt.subplot(131)
plt.title('sales - day')
# data_grouped_day.plot(kind='bar')
sns.barplot(data=data_grouped_day, palette=sns.color_palette())plt.subplot(132)
plt.title('sales - month')
sns.barplot(data=data_grouped_month, palette=sns.color_palette())plt.subplot(133)
plt.title('sales - year')
sns.barplot(data=data_grouped_year, palette=sns.color_palette());

由表可知：

• 单日中，周六和周日的销售额最高，周四最低。
• 月份中，12 月的销售额最高。
• 年份中，销售额呈现逐年上升的趋势，后面会单独研究趋势。

5. 滞后特征分析

avg_sales = train.groupby('date').agg({'sales': 'mean'}).reset_index()
avg_sales['Time'] = np.arange(len(avg_sales.index))# 创建滞后特征
avg_sales['Lag_1'] = avg_sales['sales'].shift(1)
avg_sales = avg_sales.reindex(columns = ['date','sales', 'Lag_1','Time'])
# 绘制原始值与滞后值之间的关系
fig, ax = plt.subplots()
sns.regplot(x='Lag_1', y='sales', data=avg_sales, ci=None, line_kws={'color':'red','linewidth':3})
# 表示 x 轴和 y 轴的单位长度相同
ax.set_aspect('equal')
plt.title('Lag Plot of Hardcover Sales');

由图可知，当天的销售额与前一天的销售额 Lag_1 正相关相关，即某一天的高销售额通常也意味着第二天的高销售额。

---

下面绘制不同滞后特征的关系图及PACF（偏自相关函数）图，PACF图用于表明在控制了其他所有滞后影响的情况下，当前值与特定过去值之间的直接关系有多强，横轴表示滞后阶数，纵轴表示偏自相关系数，范围从-1到1，绝对值越大表示相关性越强。
特征：

• 截尾：在某个滞后期后，偏自相关系数迅速降为零。这表明该时间序列可能具有自回归（AR）特性。
• 拖尾：偏自相关系数逐渐衰减。这表明该时间序列可能具有移动平均（MA）特性。

# plot_lags()函数此处省略，函数定义见gitee代码文件
_ = plot_lags(avg_sales.sales, lags=12, nrows=2)
_ = plot_pacf(avg_sales.sales, lags=12)

滞后图表明销售额与其滞后的关系在某种程度上是线性的，而PACF图表明可以使用滞后 1、3、5、6、7、8 和 9 来捕获依赖关系。PACF图在滞后1处有一个峰值，然后迅速下降至几乎为零，表明这是一个AR(1)模型。

6. 趋势分析

建模前，需要对数据的趋势（固定窗口内的平均值）进行分析，根据趋势的类型（线性或者非线性）选用合适的模型进行建模。趋势以日为单位，因此在后面数据处理部分需要将原数据转为一日一行。

avg_sales = train.groupby('date').agg({'sales': 'mean'})
#------------------------------------------------------------------------------------------------------------#
# 绘制移动平均图
# rolling(...) 是 Pandas 中用于计算滚动统计量的函数
# window：窗口大小
# center：将计算的平均值放在窗口的中心位置
# min_periods：设置窗口内至少需要的有效数据点数量，该参数通常设置为窗口大小的一半，以确保在计算平均值时有足够的数据
# mean：计算滚动窗口内的平均值
#------------------------------------------------------------------------------------------------------------#
moving_average = avg_sales.rolling(window=365,       center=True,      min_periods=183,  
).mean()              ax = avg_sales.plot(style=".",figsize=(10, 4), title="Tunnel Traffic - 365-Day Moving Average")
moving_average.plot(ax=ax, linewidth=3,  label='Moving Average'
);
ax.legend(["Sales", "Moving Average"], loc="upper left");

由图可知，销售额整体呈线性上升趋势。

---

利用线性回归来拟合趋势：

from statsmodels.tsa.deterministic import DeterministicProcess
#------------------------------------------------------------------------------------------------------------#
# 生成时间序列特征，通过该特征，模型能够捕捉到趋势的变化，
# 可以弥补一些算法无法学习趋势（如 XGBoost 和随机森林）的缺点
#------------------------------------------------------------------------------------------------------------#
dp = DeterministicProcess(index=avg_sales.index,  # 使用 avg_sales 的索引作为特征生成的基础constant=True,         # 添加常数项（截距）order=1,               # 生成一个线性趋势项，如果 order=2，则会再添加一个二次趋势项drop=True,            # 如果生成的特征之间存在多重共线性，则会自动删除某些特征
)
# 特征生成
X = dp.in_sample()# 利用线性模型拟合趋势特征
from sklearn.linear_model import LinearRegression
y = avg_sales["sales"]  
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
y_pred = pd.Series(model.predict(X), index=X.index)ax = avg_sales.plot(style=".", title="sales - Linear Trend", figsize=(10, 4))
y_pred.plot(ax=ax, linewidth=3);
ax.legend(["Sales", "Linear Trend"], loc="upper left");

利用DeterministicProcess生成未来180（天）个时间点的特征，预测其趋势：

X = dp.out_of_sample(steps=180)# 获取最后一个日期
last_date = avg_sales.index[-1]  
# pd.Timedelta(days=1)：时间增量，表示 1 天
# freq='D'：日期频率，表示按天生成日期
future_dates = pd.date_range(start=last_date + pd.Timedelta(days=1), periods=180, freq='D')
# 设置新索引
X.index = future_datesy_fore = pd.Series(model.predict(X), index=X.index)
ax = avg_sales.plot(title="Sales- Linear Trend Forecast", style=".-", figsize=(14, 6))
y_pred.plot(ax=ax, linewidth=3, label="Trend")
y_fore.plot(ax=ax, linewidth=3, label="Trend Forecast", color="C3")
ax.legend();

7. 季节性分析

当一个时间序列的观测值有规律的周期性变化时，时间序列就会表现出季节性。季节性的变化通常是遵循时间的——以一天、一周或一年为单位重复。这里介绍两种关于季节性的特征。 第一种是指示器（indicators），适合季节性周期中观测值较少的情况，例如基于每天观测值的周季节性。 第二种是傅里叶特征（Fourier features），适合季节性周期中观测值较多的情况，例如基于每天观测值的月/年季节性。下面以周和年的视角查看销售额的季节性变化：

"""
绘制季节性波动图
Params：X：        数据集y：        目标变量（销售额）period：   时间间隔freq：     时间频率ax：       图形对象
Returnsax：       图形对象
"""
def seasonal_plot(X, y, period, freq, ax=None):if ax is None:_, ax = plt.subplots()palette = sns.color_palette("husl", n_colors=X[period].nunique())ax = sns.lineplot(x=freq,y=y,hue=period,data=X,ci=False,ax=ax,palette=palette,legend=False,)ax.set_title(f"Seasonal Plot ({freq} of {period})")# 遍历绘制的每条线和对应的唯一 period 名称# 这里会出现周数相同的情况（因为跨了好几个年份），相同的周数取均值for line, name in zip(ax.lines, X[period].unique()):# 获取当前线的 y 数据的最后一个值y_ = line.get_ydata()[-1]# 在图上为每条线添加注释ax.annotate(name,xy=(1, y_),xytext=(6, 0),                   # 注释文本的偏移量color=line.get_color(),          # 注释文本的颜色与线条颜色一致xycoords=ax.get_yaxis_transform(),# 使用 y 轴的比例进行坐标转换textcoords="offset points",      # 注释文本的位置将相对于指定的坐标点进行偏移size=14,va="center",)return ax
"""
绘制周期图
Params：X：        数据集y：        目标变量（销售额）period：   时间间隔freq：     时间频率ax：       图形对象
Returnsax：       图形对象
"""
def plot_periodogram(ts, detrend='linear', ax=None):from scipy.signal import periodogram
#     fs = pd.Timedelta("1Y") / pd.Timedelta("1D")fs = 365 freqencies, spectrum = periodogram(ts,fs=fs,detrend=detrend,window="boxcar",scaling='spectrum',)if ax is None:_, ax = plt.subplots()ax.step(freqencies, spectrum, color="purple")ax.set_xscale("log")ax.set_xticks([1, 2, 4, 6, 12, 26, 52, 104])ax.set_xticklabels([  "Annual (1)",           # 1：每年重复一次的周期"Semiannual (2)","Quarterly (4)","Bimonthly (6)",        # 6：每年重复六次的周期"Monthly (12)","Biweekly (26)","Weekly (52)","Semiweekly (104)",],rotation=30,)ax.ticklabel_format(axis="y", style="sci", scilimits=(0, 0))ax.set_ylabel("Variance")ax.set_title("Periodogram")return ax

X = avg_sales.copy().reset_index()
X['date'] = pd.to_datetime(X['date'])
# DatetimeIndex 对象没有 week 属性，因此需转为 PeriodIndex
X = X.set_index('date').to_period("D")# 返回一周中的第几天，范围是 0（周一）到 6（周日）
X['day'] = X.index.dayofweek 
# 返回日期的周数
X['week'] = X.index.week # 返回一年中的第几天
X['dayofyear'] = X.index.dayofyear
# 返回年数
X['year'] = X.index.year
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(11, 8))# 从周和年的视角查看销售额的季节性变化
seasonal_plot(X, y="sales", period="week", freq="day", ax=ax0)
seasonal_plot(X, y="sales", period="year", freq="dayofyear", ax=ax1);
# 调整子图上下间距
plt.subplots_adjust(hspace=0.3)

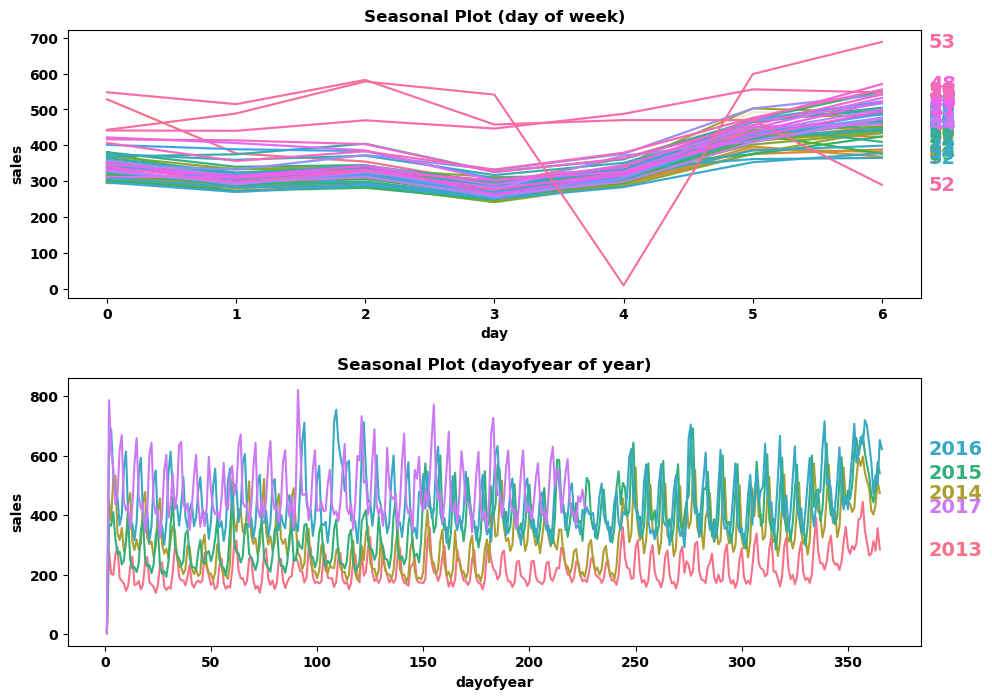
由图知，，周四的销售额最低，周一到周四的销售额逐渐递减，周四到周天的销售额逐渐递增；不同年份全年的销售额较为稳定。

---

绘制周期图（纵坐标为方差）：

#------------------------------------------------------------------------------------------------------------#
# 绘制周期图
#------------------------------------------------------------------------------------------------------------#
fig, ax = plt.subplots(1,1,figsize=(10, 5))
ax = plot_periodogram(avg_sales.sales, ax = ax);

周（Weekly）的季节性最强（作为指示器），峰值表示在该频率下时间序列的方差较大，意味着在每周的特定时间点，数据的变化幅度较大（周四销售额最低，且周一到周四递减，周四到周天递增）。此外，年度和双周也有一些季节性，有数据集的注释可知，公共部门的工资每两周支付一次，即每月的 15 日和最后一天，这解释了双周的季节性。基于周期图，我们使用指示器来建模周季节性，使用傅里叶特征来建模年季节性。

8. 节假日分析

分析节假日的销售额是否比工作日的高。

holidays_events = holiday.copy()
holidays_events['date'] = pd.to_datetime(holidays_events['date'])
# 去除已被转移的假期和被宣布为工作日的假期
holidays_events= holidays_events.loc[(holidays_events.transferred==False) & (holidays_events.type != 'Work Day')]
# 移除重复日期的节日
holidays_events=holidays_events.drop_duplicates(subset='date')  # National 和 Regional 类型节日的销售额
fig, axes = plt.subplots(2, 1, figsize=(12,10))
NRHolidays=holidays_events.loc[holidays_events['locale']!='Local',:]
#------------------------------------------------------------------------------------------------------------#
# 以'data'列为基准列，合并两个 DataFrame 数据
# how='left': 左连接，即保留左边DataFrame（avg_sales）的所有行
#------------------------------------------------------------------------------------------------------------#
# avg_sales.index = avg_sales.index.to_timestamp()
NRHolidays_avg_sales=avg_sales.reset_index().merge(NRHolidays, on='date', how='left')
x_cor=NRHolidays_avg_sales.loc[NRHolidays_avg_sales['type'].notna(),'date'].values
y_cor=NRHolidays_avg_sales.loc[NRHolidays_avg_sales['type'].notna(),'sales'].valuesavg_sales['sales'].plot(style=".-", ax=axes[0])
# plot_date(): 用于绘制日期数据的函数
axes[0].plot_date(x_cor, y_cor,color='C3', label='National / Regional Holiday')
axes[0].set_ylabel('Avg. Sales')
axes[0].set_title('Avg. Sales At National and Regional Holidays Only')
axes[0].legend()# LocalHolidays 类型节日的销售额
LHolidays=holidays_events.loc[holidays_events['locale']=='Local',:]
LHolidays_avg_sales=avg_sales.reset_index().merge(LHolidays,on='date',how='left')
x_cor=LHolidays_avg_sales.loc[LHolidays_avg_sales['type'].notna(),'date'].values
y_cor=LHolidays_avg_sales.loc[LHolidays_avg_sales['type'].notna(),'sales'].values
_=avg_sales['sales'].plot(style='.-',ax=axes[1])
axes[1].plot_date(x_cor,y_cor,color='C3', label='Local Holiday')
axes[1].set_ylabel('Avg. Sales')
axes[1].set_title('Avg. Sales At Local Holidays')
axes[1].legend()plt.subplots_adjust(hspace=0.3)
plt.show()

当地节假日的销售额与其他天相似，而国家和地区节假日的销售额普遍比其他天高。由于我们的目的是分析节假日的销售额是否比工作日的高，因此可以移除 Local 类型的节假日。

holidays_events= holidays_events[holidays_events.locale!='Local']
#------------------------------------------------------------------------------------------------------------#
# 合并训练集和“holidays_events”数据集，并在新的合并数据集上创建新的假日指标列，该列采用两个值：
#  0 表示工作日
#  1 表示节假日（含周末）
#------------------------------------------------------------------------------------------------------------#
train_eda = train.copy()
holidays_events=holidays_events[['date','type']] train_eda=pd.merge(left=train_eda, right=holidays_events, on='date', how='left')# 列名重命名
train_eda.rename({'type':'is_holiday'},axis=1,inplace=True)
# 列值重映射
train_eda['is_holiday']=train_eda.is_holiday.map({'Holiday':1,'Additional':1,'Event':1,'Bridge':1,'Transfer':1}).fillna(0).astype('int8')# 将周末标识为 1
train_eda.set_index('date', inplace=True)
train_eda['day_of_week']=train_eda.index.dayofweek.astype('int8')
train_eda.loc[(train_eda['day_of_week']==5) | (train_eda['day_of_week']==6), 'is_holiday']=1# 通过图表发现每年的第一天（新年）的销售额都很低，接近于0，虽然是节假日，但是为了不影响整体的销售额分析（节假日整体销售额较高），
# 特将其当作异常值，标记为工作日
train_eda['day_of_year']=train_eda.index.dayofyear
train_eda.loc[train_eda['day_of_year']==1 ,'is_holiday']=0# 节假日的每日平均销售额
avg_sales_holiday=train_eda[train_eda.is_holiday==1].groupby('date')['sales'].mean() 
# 工作日的每日平均销售额
avg_sales_workday=train_eda[train_eda.is_holiday==0].groupby('date')['sales'].mean() 
plt.figure(figsize=(12,5))
avg_sales_workday.plot(color='0.4',style='.', legend=True, label='Workday Avg. Sales')
avg_sales_holiday.plot(color='red',style='.', legend=True, label='Holiday Avg. Sales')
plt.xlabel('Date')
plt.ylabel('Avg. Sales')
plt.title('Avg. Sales on Holidays vs. Workdays')
plt.show()

节假日和工作日的销售额之间的分层明显，差异较大。即 is_holiday 列能有效区分出销售额，因此将 is_holiday 列作为训练变量。

9. 商店分析

avg_sales=train.groupby('store_nbr')['sales'].mean().reset_index()
stores=store.merge(avg_sales, on='store_nbr', how='left')plt.figure(figsize=(16,16))
# 绘制各商店在不同州的平均销售情况
plt.subplot(2,2,1)
state_grouped=stores.groupby('state')['sales'].mean().sort_values(ascending=False)
sns.barplot(x=state_grouped.index, y=state_grouped.values, palette='rocket', order=list(state_grouped.index))
plt.xlabel('')
plt.xticks(rotation=45)
plt.ylabel('Avg. Sales')
plt.title('Avg. Sales by State')# 绘制不同类型商店的平均销售情况
plt.subplot(2,2,2)
type_grouped=stores.groupby('type')['sales'].mean().sort_values(ascending=False)
plt.pie(type_grouped, labels=type_grouped.index, autopct="%1.1f%%")
# 使 x 轴和 y 轴长度相等
plt.axis('equal')
plt.title('Avg. Sales by Store Type')# 绘制商店不同组合类型的平均销售情况
plt.subplot(2,2,3)
cluster_grouped=stores.groupby('cluster')['sales'].mean().sort_values(ascending=False)
plt.pie(cluster_grouped, labels=cluster_grouped.index, autopct="%1.1f%%")
# 使 x 轴和 y 轴长度相等
plt.axis('equal')
plt.title('Avg. Sales by Store Cluster')# 绘制各商店在不同城市的平均销售情况
plt.subplot(2,2,4)
city_grouped=stores.groupby('city')['sales'].mean().sort_values(ascending=False)
sns.barplot(x=city_grouped.index, y=city_grouped.values, palette='rocket', order=list(city_grouped.index))
plt.xlabel('')
plt.xticks(rotation=45)
plt.ylabel('Avg. Sales')
plt.title('Avg. Sales by City')
plt.subplots_adjust(hspace=0.5)
plt.show()

由图可知：

• 卖得最好的三个州分别是 Pichincha 、Tungurahua 和 Loja，卖得最差的三个州分别是 Cotopaxi、Manabi 和 Pastaza。
• 卖得最好的三个城市分别是 Quito、Cayambe 和 Ambato，卖得最差的三个城市分别是 Playas、Manta 和 Puyo。
• 卖得最好的四种 Store Clusters 为（5， 14， 8， 11），卖得最差的四种 Store Clusters 为（7， 3， 15， 16）
• 最佳商店类型的顺序为：A - D - B - E - C

这些变量都会对超市的销售额产生影响，因此 store_nbr 列也作为训练变量。

10. 订单量分析

transaction 数据集中包含商店在指定日期的订单数（发票数），这与销售额高度相关。由于订单量仅训练集有，因此仅对订单量数据集作数据分析，不作为训练变量。

#-----------------------------------------------------------------------------------------------------#
# 计算每天的平均销售额（包含所有商店和所有产品类型）
# .agg({'sales': 'mean'})：对每个日期的销售额计算平均值，agg() 用于对分组后的数据进行聚合操作
#-----------------------------------------------------------------------------------------------------#
avg_sales = train.groupby('date').agg({'sales': 'mean'}).reset_index()#-----------------------------------------------------------------------------------------------------#
# 计算每天订单量的均值以及周均值
#-----------------------------------------------------------------------------------------------------#
avg_transactions = trans.groupby('date').agg({'transactions': 'mean'}).reset_index()
avg_transactions['weekly_avg_transactions'] = avg_transactions['transactions'].ewm(span=7, adjust=False).mean()
ax2 = avg_transactions.plot(x= 'date', y= ['transactions', 'weekly_avg_transactions'], figsize=(18,6))
plt.title('Transactions & Weekly_avg_transactions');

# 统计各商店每天的销售总额
avg_sales = train_eda.groupby(['date','store_nbr'])['sales'].mean().reset_index()
temp = pd.merge(avg_sales, trans, how = "left", on=['date', 'store_nbr']).fillna(0)print('总交易额与订单数量之间的相关系数: ',np.round(temp[['sales','transactions']].corr().iloc[0,1],4),'\n')sns.regplot(data=temp, x='transactions', y='sales', line_kws={'color':'red','linewidth':3})
plt.xlabel('Transactions')
plt.ylabel('Total. Sales')
plt.title('Total. Sales vs Transactions')
plt.show()

输出结果：

总交易额与订单数量之间的相关系数:  0.854 

每日的订单数与销售总额呈显著正相关。

plt.figure(figsize=(12,5))
sns.lineplot(data=temp,x='date', y='transactions', hue='store_nbr')
plt.show()

各商店每年的订单量数量波动不大，且商店订单量在年底会增长。

---

可视化各商店的平均订单数和平均销售额：

plt.figure(figsize=(16,10))plt.subplot(211)
store_trans = temp.groupby('store_nbr')['transactions'].mean().sort_values(ascending=False).to_frame()
sns.barplot(data=store_trans, x=store_trans.index, y='transactions', palette='rocket',order=list(store_trans.index))plt.subplot(212)
store_sales = temp.groupby('store_nbr')['sales'].mean().sort_values(ascending=False).to_frame()
sns.barplot(data=store_sales, x=store_sales.index, y='sales', palette='rocket', order=list(store_sales.index));

可以发现，订单数越高的商店，销售额也越高。

11. 特征工程

后面的训练结果表明，仅使用2017年的数据拟合的结果比使用所有训练数据拟合的结果要好，因此此处进选取2017年的数据作为训练集。利用 DeterministicProcess 方法生成趋势特征、季节性特征（短期）和傅里叶特征（长期）。此外，Biweekly (26)、Weekly (52) 和Semiweekly (104)由于观测值较少，一般作为指示器。但 Annual (1)、Semiannual (2)、Quarterly (4)观测值较多且季节性强，可以用傅里叶特征进行建模，为了捕捉这三个周期的季节性特征，这里使用4阶傅里叶级数来近似特征。注：更高的阶数可以捕捉到更复杂的季节性特征，但也可能导致过拟合，需合理选择阶数。

from statsmodels.tsa.deterministic import DeterministicProcess, CalendarFourierstore_sales = train.drop('id',axis=1).set_index(['store_nbr','family','date'])
#-----------------------------------------------------------------------------------------------------#
# unstack(['store_nbr','family']): 将行索引 store_nbr 和 family 转换为列索引，形成一个新的 DataFrame，
# 其中行索引为 date，列索引为 store_nbr 和 family 的组合
#-----------------------------------------------------------------------------------------------------#
# family_sales = store_sales.drop('onpromotion', axis=1).unstack(['store_nbr','family'])
family_sales = store_sales.drop('onpromotion', axis=1).unstack(['store_nbr','family']).loc['2017']
# 为dp方法设置时间频率
family_sales.index = family_sales.index.to_period('D')
y = family_sales.loc(axis=1)['sales']
#-----------------------------------------------------------------------------------------------------#
# CalendarFourier 用于生成傅里叶项，用来捕捉时间序列中的复杂周期性
# freq='M'：按月采样（因为月的季节性最明显）
# order=4：使用傅里叶级数的前 4 个阶数来近似年度季节性
# 每个阶数会生成一组正弦项和余弦项，总共生成 2 * order = 8 个傅里叶项
#-----------------------------------------------------------------------------------------------------#
fourier = CalendarFourier(freq='M', order=4) #-----------------------------------------------------------------------------------------------------#
# 生成趋势特征、季节性特征和傅里叶特征
# DeterministicProcess 用于生成包含时间序列趋势和季节性特征的设计矩阵
# order=1 表示线性趋势
# additional_terms：添加额外的傅里叶特征
# drop=True：如果生成的特征之间存在多重共线性，则会自动删除某些特征
# seasonal = True生成（生成短期季节性）季节性特征（如每周），傅里叶级数（sin/cos）捕捉更长周期的季节性（如月度、年度）。
# 对于日频数据，默认生成每周的季节性变量（7个二元变量，对应星期一到星期日）
#-----------------------------------------------------------------------------------------------------#
dp =  DeterministicProcess(index = y.index, seasonal = True,                      order = 1, additional_terms = [fourier], drop = True)
X_train = dp.in_sample()print(f"        y的大小：{y.shape}")
print(f"X_train_1的大小：{X_train.shape}")

        y的大小：(227, 1782)
X_train_1的大小：(227, 16)

训练集节假日数据处理：

# 移除已被转移的假期和被宣布为工作日的假期
holidays_events= holiday.loc[(holiday.transferred==False) & (holiday.type != 'Work Day') & (holiday.locale != 'Local')]
# 移除重复日期的节日
holidays_events.drop_duplicates('date', inplace=True)
holidays_events = holidays_events[['date','type']]# 合并训练集与 holidays 数据集
X_train.index = X_train.index.to_timestamp()
X_train=X_train.reset_index().merge(holidays_events, on='date',how='left')
X_train.rename({'type':'is_holiday'}, axis=1, inplace=True)
X_train['is_holiday']=X_train.is_holiday.map({'Holiday':1, 'Transfer':1, 'Additional':1,'Bridge':1, 'Event':1})
X_train['is_holiday']=X_train['is_holiday'].fillna(0)# 将周末标识为 1
X_train['day_of_week'] = X_train.date.dt.day_of_week.astype('int8')
X_train.loc[(X_train['day_of_week']==5) | (X_train['day_of_week']==6), 'is_holiday'] = 1
X_train.drop('day_of_week',axis=1, inplace=True)#-----------------------------------------------------------------------------------------------------#
# 通过图表发现每年的第一天（新年）的销售额都很低，接近于0，虽然是节假日，
# 但是为了不影响整体的销售额分析（节假日整体销售额较高），特将其当作异常值，标记为工作日
#-----------------------------------------------------------------------------------------------------#
X_train['start_of_year']= (X_train.date.dt.dayofyear ==1)
X_train.loc[X_train['start_of_year']==True, 'is_holiday']=0
X_train = X_train.set_index('date')
X_train.index = X_train.index.to_period('D')#------------------------------------------------------------------------------------------------------------#
# 划分训练集和验证集
# 将2013-01-01到2017-07-15的数据划分为训练姐，2017-07-16到2017-08-15划分为验证集
#------------------------------------------------------------------------------------------------------------#
train_end = '2017-07-15'
val_start = '2017-07-16'
X_train_1 = X_train[:train_end]
X_val_1 = X_train[val_start:]
y_train = y[:train_end]
y_val = y[val_start:]

12. 模型搭建

线性回归擅长推断趋势，但无法学习变量间的交互关系。CATBoost 擅长学习变量间的交互关系，但无法推断趋势。因此使用线性回归和 CATBoost 混合模型来预测结果，利用这两种模型互相弥补弱点。具体过程如下：

1. 使用线性模型进行训练和预测
   linear.fit（X_train_1， y_train）
y_pred_1 = linear.predict(X_val_1)

2. 使用残差模型进行训练和预测
   catboost.fit（X_train_2， y_val - y_pred_1）
y_pred_2 = catboost.predict（X_train_2）

3. 相加得到最终预测值
   y_pred = y_pred_1 + y_pred_2

代码实现如下：

from catboost import CatBoostRegressor
"""
混合模型训练
Params：linear：      线性模型catboost：    catboost模型X_train_1：   模型1上的训练集X_train_2:    模型2上的训练集y：           模型1训练集的目标值
Output：混合模型拟合
"""
def fit(linear, catboost, X_train_1, X_train_2, y):print("模型训练中.......")linear.fit(X_train_1, y)#----------------------------------------------------------------------------------------------------## 目标数据y（227 rows × 1782 columns）共1782列，每一列都会使用全部227行的特征数据# X_train_1（227 rows × 18 columns）# 因此最终训练的权重数据大小为(1782, 18)，可以理解为共训练了1782个模型#----------------------------------------------------------------------------------------------------## 这里不指定columns=y.columns的话，列名默认从0开始递增，y_fit大小为(227, 1782)y_fit = pd.DataFrame(linear.predict(X_train_1), index=X_train_1.index, columns=y.columns)
#     print(y_fit.shape)y_resid = y - y_fit#-----------------------------------------------------------------------------------------------------## 宽转长，将原来的列索引['store_nbr','family']转为行索引，并重新编制索引# 因为需要转换时间格式，因此先重置索引，把 date 列转为 datetime 格式#-----------------------------------------------------------------------------------------------------#y_resid = y_resid.stack(['store_nbr','family']).reset_index()#-----------------------------------------------------------------------------------------------------## 将日期时间数据转换为 datetime 对象，否则在使用 reindex 日期匹配时，会因为类型不匹配而导致无法找# 到对应的索引，最终导致 residuals 列的值为 NaN。# pandas 不允许直接将 PeriodDtype 数据转换为 datetime，需要先将 Period 转换为 Timestamp。#-----------------------------------------------------------------------------------------------------#y_resid['date'] = y_resid['date'].dt.to_timestamp()y_resid['date'] = pd.to_datetime(y_resid['date'])# date 列转为 datetime 格式后，重新设置索引y_resid = y_resid.set_index(['store_nbr','family','date'])y_resid.rename({0:'residuals'},axis=1,inplace=True)# y_resid 此时第一列到第三列分别是store_nbr，family，date，这与原数据集train不一致，因此需要借助原数据集的顺序来编排new_index=X_train_2.copy()# 将编码后的特征还原new_index['family']=le.inverse_transform(new_index['family']) new_index=new_index.reset_index().set_index(['store_nbr','family','date'])#  将 y_pred 数据集按照 new_index 的索引重新排序（与原数据集顺序一致）y_resid = y_resid.reindex(new_index.index)# 将'store_nbr'和'family'的列从索引转换回普通列，并移除，只留下‘date’作为索引y_resid.reset_index(['store_nbr','family'],drop=True,inplace=True)
#     print(y_resid)catboost.fit(X_train_2, y_resid)print("模型训练结束！")"""
混合模型预测
Params：linear：      线性模型catboost：    catboost模型X_train_1：   模型1上的训练集X_train_2:    模型2上的训练集
Returns:y_pred:       混合模型的最终预测值
"""
def predict(linear, cat, X_train_1, X_train_2):print("模型预测中.......")global y y_pred = pd.DataFrame(linear.predict(X_train_1), index=X_train_1.index, columns=y.columns)# 将原来的列索引['store_nbr','family']转为行索引，并重新编制索引y_pred = y_pred.stack(['store_nbr','family']).reset_index()y_pred['date'] = y_pred['date'].dt.to_timestamp()
#     y_pred['date'] = pd.to_datetime(y_pred['date'])y_pred = y_pred.set_index(['store_nbr','family','date'])y_pred.rename({0:'sales'}, axis=1, inplace=True)# y_resid 此时的数据排序方式与原数据集train不一致，因此需要借助原数据集的顺序来编排new_index=X_train_2.copy()new_index['family']=le.inverse_transform(new_index['family']) new_index=new_index.reset_index().set_index(['store_nbr','family','date'])y_pred = y_pred.reindex(new_index.index)values = y_pred['sales'].values# 残差值 + 原始预测值sales = catboost.predict(X_train_2) + values# 将所有小于 0 的值替换为 0，大于或等于 0 的值保持不变y_pred['sales'] = sales.clip(0.0) print("模型预测结束！")return y_pred 

from sklearn.preprocessing import LabelEncoder
from sklearn.linear_model import LinearRegressionlinear = LinearRegression() 
# silent=True：不输出训练信息
catboost = CatBoostRegressor(silent=True) 
train_2 = train.drop(['id','sales'],axis=1).set_index('date').loc['2017']
# 合并油价
train_2 = train_2.merge(oil, on='date', how='left')
train_2.rename({'dcoilwtico':'oil_price'},axis=1,inplace=True)
#-----------------------------------------------------------------------------------------------------#
# fillna(method='ffill'): 使用前一个值填充缺失值
# fillna(method='bfill')：使用后一个值填充缺失值
#-----------------------------------------------------------------------------------------------------#
train_2['oil_price']=train_2['oil_price'].fillna(method='ffill').fillna(method='bfill')
X_train_2 = train_2[:train_end]
X_val_2   = train_2[val_start:]# 将分类变量转换为整数标签,（适用于有序分类变量，无序数据还是用独热更好）
le = LabelEncoder()
X_train_2['family'] = le.fit_transform(X_train_2['family'])
X_val_2['family'] = le.fit_transform(X_val_2['family'])fit(linear, catboost, X_train_1, X_train_2, y_train)
y_pred= predict(linear, catboost, X_val_1, X_val_2)

# 将y_val的格式与y_pred统一
y_val_metric = y_val.stack(['store_nbr','family']).reset_index()
y_val_metric = y_val_metric.set_index(['store_nbr','family','date'])
y_val_metric.rename({0:'sales'},axis=1,inplace=True)from sklearn.metrics import mean_squared_log_error
rmsle = np.sqrt(mean_squared_log_error(y_val_metric.reset_index()['sales'], y_pred.reset_index()['sales']))
print("RMSLE: {}".format(rmsle))

输出结果：

RMSLE: 1.2832379257524276

y_val_avg = y_val_metric.groupby('date')['sales'].mean()
y_val_avg = y_val_avg.reset_index()
# 针对时间序列数据，使用 lineplot 时，x 轴需为 datetime 类型，以便正确处理
y_val_avg['date'] = y_val_avg['date'].dt.to_timestamp()# y_pred_avg['date']已经是datetime类型
y_pred_avg = y_pred.groupby('date')['sales'].mean()
y_pred_avg = y_pred_avg.reset_index()
avg_sales = train.groupby('date').agg({'sales': 'mean'})
avg_sales_2017 = avg_sales.loc['2017']
avg_sales_2017 = avg_sales_2017.reset_index()plt.figure(figsize=(14,5))
sns.lineplot(data=avg_sales_2017, x='date', y = "sales",label ="actual")
sns.lineplot(data=y_pred_avg, x='date', y = "sales", label ="pred", color = 'red');

测试集节假日数据处理：

X_test_1 = dp.out_of_sample(steps = 16) 
X_test_1.index = X_test_1.index.rename('date')# 移除已被转移的假期和被宣布为工作日的假期
X_test_1=X_test_1.reset_index().merge(holidays_events,on='date',how='left').set_index('date')
X_test_1.rename({'type':'is_holiday'}, axis=1, inplace=True)
X_test_1['is_holiday']=X_test_1.is_holiday.map({'Holiday':1, 'Transfer':1, 'Additional':1,'Bridge':1, 'Event':1})
X_test_1['is_holiday']=X_test_1['is_holiday'].fillna(0)# 将周末标识为 1
X_test_1['day_of_week'] = X_test_1.index.day_of_week
X_test_1.loc[(X_test_1['day_of_week']==5) | (X_test_1['day_of_week']==6), 'is_holiday'] = 1
X_test_1.drop('day_of_week',axis=1, inplace=True)#-----------------------------------------------------------------------------------------------------#
# 通过图表发现每年的第一天（新年）的销售额都很低，接近于0，虽然是节假日，
# 但是为了不影响整体的销售额分析（节假日整体销售额较高），特将其当作异常值，标记为工作日
#-----------------------------------------------------------------------------------------------------#
X_test_1['start_of_year']= (X_test_1.index.dayofyear ==1)
X_test_1.loc[X_test_1['start_of_year']==True, 'is_holiday']=0X_test_2=test.copy()
X_test_2 = X_test_2.drop('id', axis = 1)
X_test_2['family'] = le.transform(test['family'])# 合并油价
X_test_2 = X_test_2.merge(oil, on='date', how='left')
X_test_2.rename({'dcoilwtico':'oil_price'},axis=1,inplace=True)
#-----------------------------------------------------------------------------------------------------#
# fillna(method='ffill'): 使用前一个值填充缺失值
# fillna(method='bfill')：使用后一个值填充缺失值
#-----------------------------------------------------------------------------------------------------#
X_test_2['oil_price']=X_test_2['oil_price'].fillna(method='ffill').fillna(method='bfill')
X_test_2 = X_test_2.set_index('date')

target = predict(linear, catboost, X_test_1, X_test_2)
print(target.reset_index()['sales'])

0          11.262400
1           6.985478
2          10.295900
3        2582.816437
4           3.753691...     
28507     362.114941
28508     115.353193
28509    1244.429034
28510      13.361938
28511      17.711126
Name: sales, Length: 28512, dtype: float64

生成提交文件

submission=pd.read_csv(path+'sample_submission.csv')
submission['sales']=target.reset_index()['sales']
# submission.to_csv('D:/Desktop/submission1.csv', index=False)
print('Submission file created!')

参考文献

[1] 时序教程
[2] 数据分析
[3] 特征工程与建模
[4*] Store Sales Forecasting | XGBOOST with RMSLE 0.375