操作系统 3.3-多级页表和快表
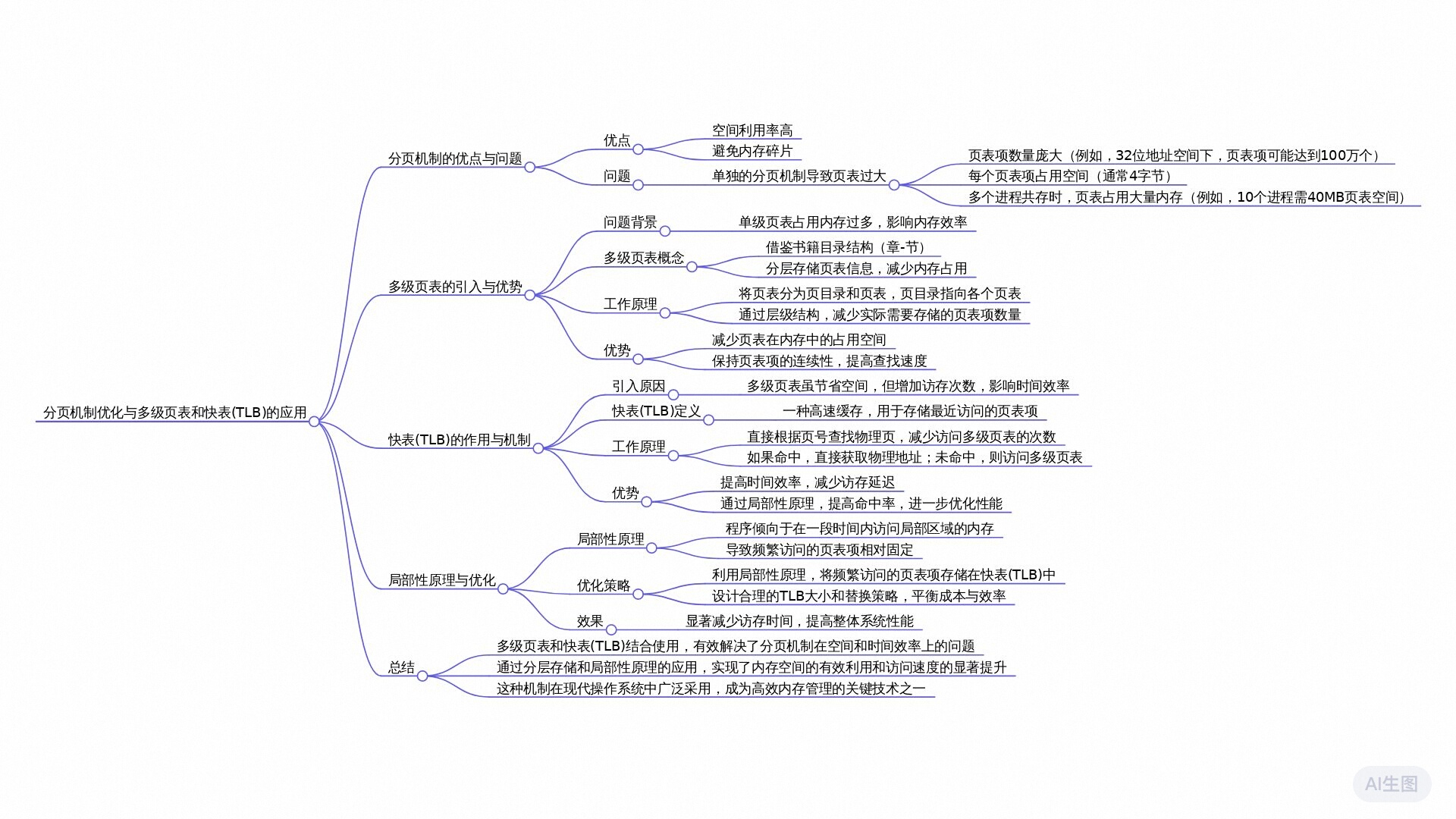
分页的问题

这张幻灯片讨论了操作系统中内存管理的一个核心问题:页大小与页表大小之间的权衡。
页(Page)是内存管理中的一个基本概念,指的是将虚拟内存分割成固定大小的块,以便于管理和访问。页的大小直接影响内存空间的利用率和页表的大小。
-
页小的优点:可以更精细地管理内存,减少内存浪费(例如,当一个进程只需要使用一小部分内存时,不需要分配一大块内存)。
-
页小的缺点:页表会变大,因为每个页都需要在页表中有一个条目。页表的大小直接影响内存管理和查找的效率
总结来说,为了提高内存空间利用率,页应该尽可能小,但这会导致页表变大,从而影响内存管理和查找的效率。操作系统设计者需要在这两者之间找到一个平衡点。
解决页表大的方案
只存到用到的页

在图中,原始页表包含4个页表项,但实际使用中第2个逻辑页没有使用,因此可以将对应的页表项删除。这样页表就从4个项减少到3个项,减少了内存占用。实际上大部分逻辑地址根本不会用到,所以可以采取这个措施。
原始页表: 页号 | 页框号 | 保护 | 有效 0 | 5 | R | 1 1 | 1 | R/W | 1 2 | | | 0 3 | 6 | R | 1 优化后的页表: 页号 | 页框号 | 保护 0 | 5 | R 1 | 1 | R/W 3 | 6 | R
通过这种方式,可以有效减少页表的大小,从而减少内存的占用,提高系统的效率。

这张幻灯片提出了一种优化页表占用内存的尝试:只存放实际用到的页。这种方法可以减少页表的大小,从而减少内存的占用。以下是幻灯片的主要内容和分析:
-
只存放用到的页:
-
只对实际使用的逻辑页创建页表项,这样可以减少页表的大小。
-
-
页号不连续的问题:
-
由于页号不连续,需要进行比较和查找,这会增加查找页表项的时间复杂度。
-
log(2^20)=20 表示在最坏情况下,可能需要进行20次查找操作。
-
-
32位地址空间和4K页面:
-
32位地址空间加上4K页面大小,理论上需要( 2^{20} )个页表项。
-
如果页号必须连续,会导致大页表占用大量内存,造成浪费。
-
-
既要连续又要让页表占用内存少:
-
需要找到一种方法,既能保持页表项的连续性,又能减少页表的内存占用。
-
幻灯片中提到了一种类比思考的方法,即用书的章目录和节目录来类比思考页表的组织方式。这种方法可以是:
单级页表
-
内存空间利用率:单级页表意味着每个虚拟页都有一个对应的页表项。在32位地址空间中,如果页的大小是4KB,那么理论上需要(2^{20})个页表项来映射整个地址空间。这会导致即使只使用了一小部分内存,页表也会占用大量空间。
-
页表的管理效率:单级页表虽然简单,但是当页表非常大时,查找特定页表项的效率会降低。此外,页表的存储也需要占用大量的内存空间,这在实际系统中可能是不可行的。
多级页表
为了解决单级页表的问题,操作系统引入了多级页表:
-
提高内存空间利用率:多级页表通过将页表本身分层次来减少必须常驻内存的页表项数量。例如,可以使用一个页目录来索引多个页表,每个页表再映射到具体的页框。这样,只有当前活跃的页表需要被加载到内存中,从而大大减少了内存的占用。
-
提高页表的管理效率:多级页表通过减少必须常驻内存的页表项数量,也减少了查找特定页表项所需的内存访问次数。这提高了页表的管理效率,尤其是在具有大量页表项的大型系统中。
多级页表

多级页表的工作原理
-
逻辑地址的分割:
-
逻辑地址被分割成多个部分,包括页目录号、页号和Offset(偏移量)。在这个例子中,逻辑地址被分为10位的页目录号、10位的页号和12位的Offset。
-
-
页目录表和页表:
-
页目录表(页目录)类似于书中的“章”,它包含了指向页表(页)的指针,页表则类似于“节”,它包含了具体的页框号和Offset,用于映射到物理地址。
-
-
页目录指针和页目录驻留内存:
-
页目录指针用于指向当前活动的页目录,页目录驻留内存表示页目录被加载到内存中。每个页目录项占用4字节。
-
-
物理地址的构建:
-
物理地址由物理页号和Offset组成。物理页号通过查找页目录和页表获得,Offset直接从逻辑地址中提取。
-
-
内存访问:
-
当需要访问一个内存地址时,首先使用页目录号在内存中查找对应的页目录项,然后使用页号在页表中查找对应的页框号,最后结合Offset计算出最终的物理地址。
-
多级页表的优势
-
减少内存占用:通过只加载当前需要的页表项,多级页表大大减少了必须常驻内存的页表项数量,从而减少了内存的占用。
-
提高查找效率:虽然多级页表增加了查找的层次,但由于每次查找只需要访问少量的页表项,因此在实际应用中,多级页表可以提高查找效率。
计算示例
-
假设有2^10个页目录项,每个页目录项占用4字节,则页目录表总共需要2^10×4字节 = 4KB。
-
如果每个页表也包含2^10个页表项,那么总共需要的内存为2^10×4×2^10字节 = 16KB,远小于单级页表所需的4MB。
快表

多级页表对时间效率的影响
-
增加访存次数:
-
相对于单级页表,多级页表虽然通过减少内存中页表项的数量提高了空间效率,但同时也增加了访问内存的次数。这是因为在多级页表结构中,需要先访问页目录,再访问页表,最后才能访问到实际的数据。
-
在64位系统中,逻辑地址空间更大,多级页表的层级可能更多,因此访问内存的次数可能会进一步增加。
-
-
TLB的作用:
-
TLB是一种高速缓存,用于存储最近或经常访问的页表项,以减少访问多级页表所需的内存访问次数。
-
TLB通过提供快速的页表项查找,减少了访问内存的时间,从而提高了系统的时间效率。
-
TLB的工作原理
-
TLB命中:
-
当CPU需要访问一个页面时,首先检查TLB中是否有对应的页表项(即TLB命中)。
-
如果TLB命中,CPU可以直接从TLB中获取物理地址,而无需访问多级页表,从而大大减少了内存访问次数。
-
-
TLB未命中:
-
如果TLB中没有对应的页表项(即TLB未命中),CPU需要访问多级页表来获取物理地址。
-
这个过程涉及到多次内存访问,包括访问页目录和页表,因此比TLB命中要慢得多。
-
-
TLB的相联性:
-
TLB通常采用相联存储结构,这意味着它可以快速地检查多个页表项,以确定是否有匹配的项。
-
这种结构使得TLB能够在很短的时间内完成查找,即使在TLB未命中的情况下,也能尽快地从多级页表中加载所需的页表项到TLB中。
-
TLB有效的原因

TLB的作用和效率
-
TLB命中时的高效率:
-
当TLB命中,即所需的页表项已经在TLB中时,内存访问的效率会很高。这是因为TLB是一种快速的缓存,可以直接提供物理地址,避免了访问主存中的页表。
-
-
TLB未命中时的效率降低:
-
当TLB未命中,即所需的页表项不在TLB中时,需要访问主存中的多级页表来获取物理地址,这会显著增加内存访问时间。
-
有效访问时间的计算
幻灯片中给出了有效访问时间的计算公式,该公式考虑了TLB命中率(HitR)和内存访问时间(MA):
有效访问时间=HitR×(TLB时间+MA)+(1−HitR)×(TLB时间+2×MA)
-
TLB时间:访问TLB所需的时间。
-
MA:访问主存所需的时间。
通过两个例子说明了不同命中率下的有效访问时间:
-
高命中率(98%):有效访问时间约为122ns。
-
低命中率(10%):有效访问时间约为210ns。
提高TLB命中率的重要性
-
实现近似访存1次:为了实现近似于直接访问内存一次的效率,TLB的命中率应该很高。
-
TLB大小与成本:虽然更大的TLB可以提高命中率,但TLB的成本也更高。因此,TLB的大小通常在64到1024条目之间。
TLB大小设置

局部性原理
-
空间局部性(Locality in Space):
-
空间局部性是指程序在执行过程中倾向于访问最近访问过的内存区域。换句话说,如果一个内存地址被访问,那么它附近的地址也很可能被访问。
-
这种局部性是由于程序中存在循环和顺序结构,导致程序在一段时间内集中访问特定的内存区域。
-
-
时间局部性:
-
时间局部性是指程序在执行过程中倾向于重复访问相同的内存地址。这种局部性是由于程序的循环结构,导致相同的内存地址在较短的时间内被多次访问。
-
TLB条目数的合理性
-
尽管系统中可能存在大量的页,但由于局部性原理,程序在任何给定时间点实际访问的页通常只占一小部分。
-
因此,一个相对较小的TLB(64到1024条目)就能有效地覆盖这些频繁访问的页,从而提高整体的内存访问效率。